Задачи по теории графов. Основные понятия и решения задач, страница 3

4).Далее мы должны рассмотреть ребра, которые имеют длину, равную семи. Два из четырех ребер следует отбросить, т.к. они вызовут появление цикла в уже построенной части дерева. Следовательно, отбросим ребра CF, BD и выберем одно из ребер - DG или FG (рис. 7).

5).min D (1⁺… 6⁺) = 2+2+3+4+6+7 = 24 У.е.

8.2.Решение задач по теории графов на ЭВМ

Рассмотрим решение простых задач на ЭВМ, затем решаем задачи 1,2,3,4 и 5.

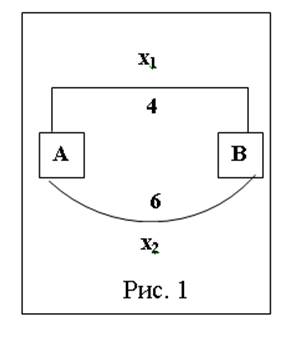
Пример. Найти кратчайший путь из двух параллельных путей, представленных на рис. 1.

Решение.1.Сведем задачу к задаче линейного программирования с булевыми переменными. Найти

,                                                               (1)

при условии

,                                                                          (2)

 или 1,                                                                       (3)

 или 1.                                                                      (4)

Ограничение (2) означает, что из двух путей должен быть выбран только один путь.

2.Оставляем ячейки В1, В2 за переменными х₁, х₂ соответственно.

3.В ячейку В3 вводим целевую функцию = 4*В1 + 6*В2.

4.В ячейку В4 введем левую часть ограничения (2) = В1 + В2.

5.Для диапазона ячеек В1:В4 устанавливаем дробный формат числа.

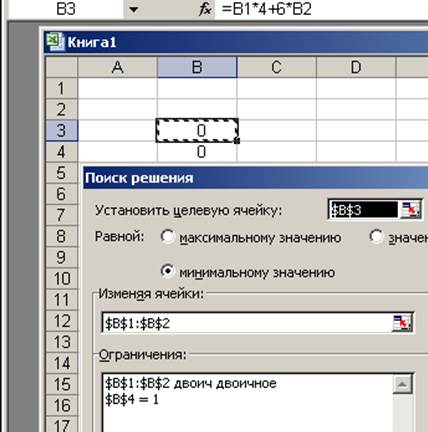
6.В диалоговом окне «Поиск решения» введем соответствующие параметры.

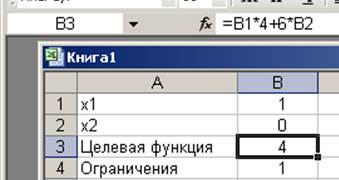
7.В результате выполнения получаем результат представленный ниже

  

Пример. Найти кратчайший путь из А в С (рис. 2).

Решение. 1.Сведем задачу к задаче линейного программирования с булевыми переменными. Найти

,                               (1)

при условии

,                                                                        (2)

,                                                                 (3)

 или 1, i=1,2,…5.                                                     (4)

Ограничения (2) и (3) означают, что из двух путей (из А в В) должен быть выбран только один путь. Аналогично и для трех путей (из В в С) также нужно выбрать только один путь.

2.Отводим для булевых переменных ячейки В2:В6.

3.В ячейку В7 вводим целевую функцию.

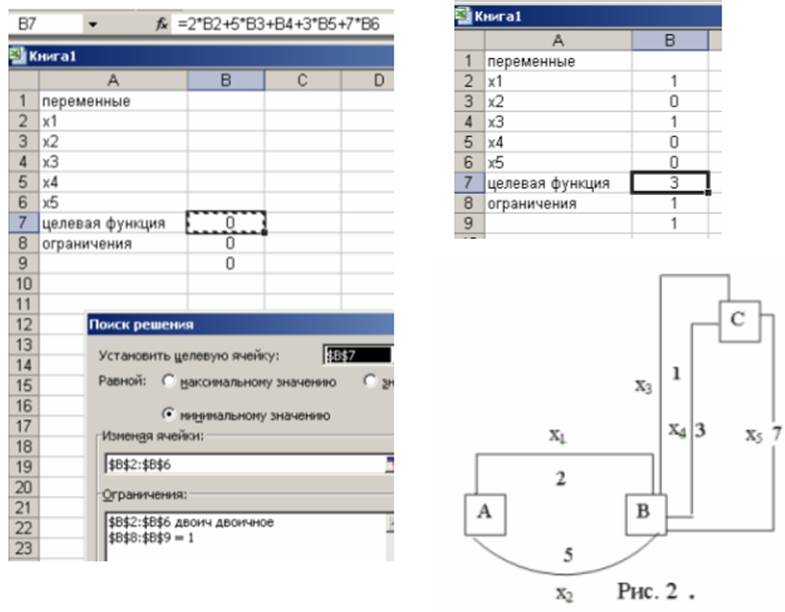
= 2*В2 + 5*В3 + В4 + 3*В5 + 7*В6.

4.В ячейки В8:В9 введем левые части ограничений (2) и (3)

= В2 + В3

= В4 + В5 + В6.

5.Для диапазона ячеек В2:В9 устанавливаем дробный формат числа.

6.В диалоговом окне «Поиск решения» введем соответствующие параметры.

И получим результат представленный выше.

Пример. Найти кратчайший путь из. А в С (рис. 3).

Решение. Предлагается читателю проверить результат самостоятельно.

min

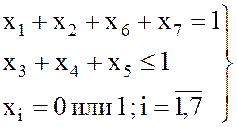 или

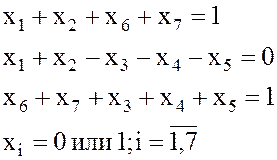
min Z(X) = 1∙x₆ = 1.

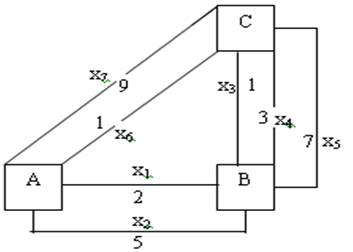
Рис. 3

Решение задачи 1 на ЭВМ

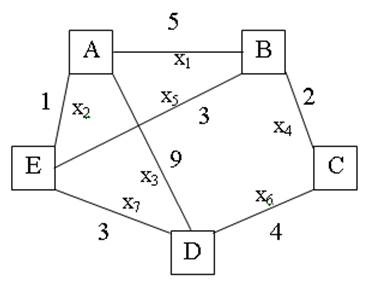Находим кратчайший путь между А и В.

1.Каждому ребру графа сопоставляем булевую (альтернативную) переменную х_i, , значение которой равно 1, если ребро входит в кратчайший путь, и равно 0 в противном случае.

2.Отводим под булевые переменные ячейки В2:В8.

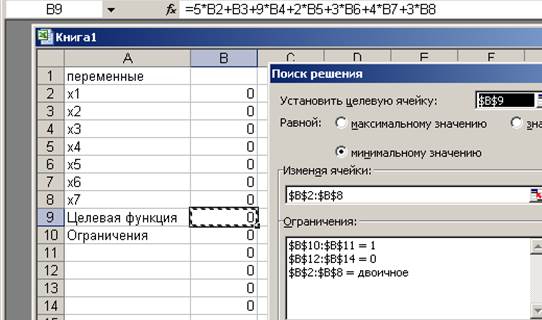
3.Вводим в ячейку В9 целевую функцию

= 5*В2 + В3 + 9*В4 + 2*В5 + 3*В6 + 4*В7 + 3*В8, которой соответствует уравнение

.

4.Вводим в ячейки В10:В14 формулы соответствующих уравнений

= В2 + В3 + В4,          ,   (т. А)

= В2 + В6 + В5,          ,   (т. В)

= В3 - В6 - В8,            ,   (т. Е)

= В4 + В8 - В7,           ,   (т. D)

= В7 – В5,                   .           (т. C)

5.Откроем диалоговое окно «Поиск решения» и установим соответствующие параметры.

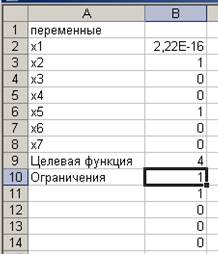
В результате получим следующее решение: А→Е→В; min Z(X) = 4.

Аналогично находим кратчайший путь между вершинами AC, AD, AE, BC, BD, BE, CD, CE, DE соответственно. Целевая функция

= 5*С2 + С3 + 9*С4 + 2*С5 + 3*С6 + 4*С7 + 3*С8.

Ограничения

= С2 + С3 + С4,          ,           (т. А)

= С5 + С7,                   ,                  (т. С)

= С3 + С6 - С8,           ,           (т. Е)

= С4 + С8 - С7,           ,           (т. D)

= С2 – С6 – С5,           .           (т. B)

Ответ: А→Е→В→С; min Z(X) = 6.

Целевая функция