Математика \ Математическое программирование

Решение многокритериальной задачи с использованием данных таблицы и линейной свертки, страница 5

3. Чем объясняется изменение интенсивности потока, переводящего многоканальные СМО (как с ожиданием, так и с отказами) из S_i₊₁ в S_i состояние?

4. Какое значение имеет интенсивность нагрузки канала для обеих систем?

5. Почему для СМО с ожиданием, неограниченной очередью вероятность отказа равна 0, а относительная пропускная способность 1?

Задание по теме 8

1. Решить задачу целочисленного линейного программирования примера 1.

2. Решить задачу целочисленного линейного программирования примера 2.

3. Задача о размещении двух пунктов материально-технического снабжения на технологической линии. При этом следует учесть следующее:

· все единицы оборудования должны находиться под контролем;

· размещение допустимо лишь в определенных местах;

· расстояние между КТП не должно быть меньше заданного;

· каждый пост должен иметь возможность обслуживать любую точку линии.

4. Дано 6 пунктов. Установить последовательность перебора пунктов, при котором длина 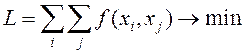. Исходные данные приведены в таблице.

Таблица

Исходные данные

f(x_i,x_j)	1	2	3	4	5	6
1	∞	1	2	3	4	5
2	2	∞	1	2	3	4
3	1	2	∞	1	2	3
4	2	1	2	∞	1	2
5	3	2	1	2	∞	1
6	1	3	2	1	2	∞

Контрольные вопросы

1. Как исходя из практических задач формулируются задачи дискретного и целочисленного программирования?

2. Какие существуют методы решения задач дискретного и целочисленного программирования?

3. Почему нельзя получить целочисленное решение округлением?

4. Пояснить алгоритм решения целочисленной задачи.

Задание по теме 9

1. Найти решение системы уравнений (9.5) для матрицы А = [2, –1; –3, –4].

2. Предлагается закупить 4 типа технологических линий. Каждая линия универсальна и может быть использована для обработки пяти изделий.

Расходы, связанные с деятельностью цеха, оплачивают заказчики. Платежи – условные стоимости обработки изделия сведены в таблицу. Задачу решить, используя линейное программирование.

Таблица

Исходные данные

Вид изделия Тип линии	1	2	3	4	5
1	200	400	600	400	700
2	300	400	600	500	800
3	400	500	600	500	800
4	700	300	500	200	100

Контрольные вопросы

1. Определить условия, при которых решение системы уравнений (9.5) оказывается справедливым, т. е P_Аи P_Вбольше нуля.

2. Какие методы, кроме линейного программирования, можно применить к решению системы (9.8)?

3. Возможна ли игровая матрица с несколькими седловыми точками?

4. Пояснить использование алгоритма линейного программирования в игровых задачах исследования операций.

1 2 3 4 5

Скачать файл