Система автоматической подстройки частоты. Оптимизация следящей системы

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт инженерной физики и радиоэлектроники

Кафедра «Радиотехники»

Курсовой проект

«Система автоматической подстройки частоты»

Пояснительная записка

Вариант №14

Проверил преподаватель:                 _________________                   

Разработал студент гр. РФ09−16:    _________________                   

Красноярск 2012г.

СОДЕРЖАНИЕ

ОБЩИЕ УКАЗАНИЯ.. 3

ИСХОДНЫЕ ДАННЫЕ. 4

ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ………………..……………..5

ОПТИМИЗАЦИЯ СЛЕДЯЩЕЙ СИСТЕМЫ……………………………………6

ЛАХ И ЛФХ СИСТЕМЫ.. 10

АЧХ ЗАМКНУТОЙ СИСТЕМЫ………………………………………………..12

МОДЕЛИРОВАНИЕ СЛЕДЯЩЕЙ СИСТЕМЫ………………………...…….13

ФУНКЦИОНАЛЬНАЯ СХЕМА СИСТЕМЫ АПЧ……………………………16

ЗАКЛЮЧЕНИЕ. 21

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 22

ОБЩИЕ УКАЗАНИЯ

Обобщенная структурная схема линейной непрерывной следящей системы 2-го порядка астатизма имеет вид, представленный на рисунке 1: 

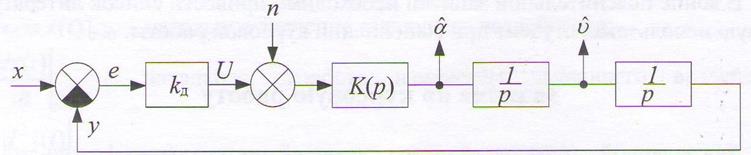
Рисунок 1 – Структурная схема следящей системы ,

Задающее воздействие определяется полиноминальной моделью

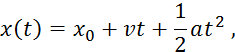
где

 – начальное значение задающего воздействия;

 – начальная скорость изменения задающего воздействия;

 – начальное ускорение.

Физический смысл и размерность параметров задающего воздействия определяются типом следящей системы.

Помеха  считается белым шумом со спектральной плотностью , имеющей размерность Вт/Гц.

Передаточная функция динамического звена описывается выражением

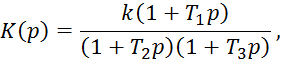
где  – общий коэффициент передачи типовых звеньев;  – постоянные времени форсирующего и инерционных звеньев.

ИСХОДНЫЕ ДАННЫЕ

Таблица 1

Таблица 2

Номер варианта	Область применения
	Следящий измеритель скорости НАП спутниковой РНС

 

1.  ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ

Для спектральной плотности эквивалентного шума n_э(t), приведенного ко входу дискриминатора (вход элемента сравнения), используя правила преобразования структурных схем (перенос сумматора с выхода на вход звена) можно записать:

   []                                  (1.1)

 

Передаточная функция динамического звена определяется выражением:

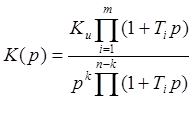                                           (1.2)

В нашем случае: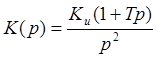                  

Передаточная функция разомкнутой системы:

                                               (1.3)

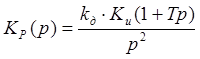
Определим передаточную функцию замкнутой системы, предварительно обозначив  :

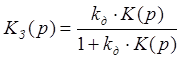                                         (1.4) 

Подставим в (1.4) результат (1.2):

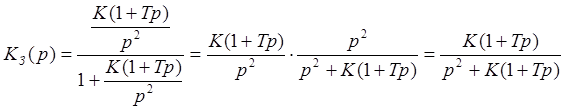         (1.5)

2. ОПТИМИЗАЦИЯ СЛЕДЯЩЕЙ СИСТЕМЫ

       Оптимизация системы по критерию минимума среднего квадрата ошибки сводится к нахождению значения параметра K_и , при котором обеспечивается минимум величины

, [Гц²]                                       (2.1)

где - составляющая, которая определяет динамическую ошибку, обусловленную инерционностью следящей системы по отношению к меняющемуся задающему воздействию

- определяет дисперсию ошибки , обусловленную помехой n(t).

Следовательно, (2.1) определяет средний квадрат результирующей ошибки

.

Динамическая ошибка  определяется параметрами  и  задающего воздействия, а также порядком астатизма (числом интеграторов) и добротностью   системы. Для системы 2-го порядка установившаяся ошибка  равна:

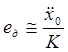,    [Гц]                                     (2.2)

где K[c^-2]- добротность системы по ускорению (k=2)

Случайная составляющая е_n(t) ошибки определяется статистическими характеристиками помехи (а также параметрами) системы. В качестве n(t) используем модель белого шума с равномерной в полосе частот от 0 до ∞ спектральной плотностью (хотя реальный шум имеет ограниченную ширину спектра, однако она во много раз превышает полосу пропускания системы F_ш , что позволяет использовать модель белого шума). Исходя из этого дисперсию шумовой ошибки рассчитаем по формуле:

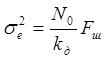                                                    ,    [Гц]                                        (2.3)

где

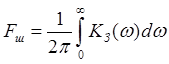                                         (2.4)

шумовая полоса следящей системы в Гц; - АЧХ замкнутой системы.

Для нахождения экстремума среднего квадрата ошибки необходимо продифференцировать выражение (2.1) по параметру К_и  и приравнять производную нулю:                                    

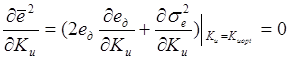                                                                       (2.5)

Для вычисления интеграла (2.4) представим подинтегральное выражение в виде

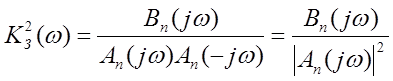,                  (2.6)                  где полиномы

                                                                 (2.7)

n- порядок дифференциального уравнения, описывающего систему.

Нахождение шумовой полосы системы и дисперсии шумовой ошибки сводится к вычислению интеграла:

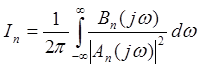,                                           (2.8)

значение которого при n=2

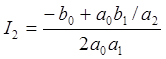                                                (2.9)

Заменим в выражении (1.5) параметр p на jω:

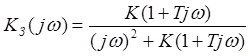                                         (2.10)

Представим данное выражение в виде (2.6):

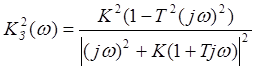,                                         (2.11)

отсюда,

В соответствии с  (2.7):    a₀=1; a₁=KT; a₂=K

b₀=-K²T²;  b₁=K²;

Подставим полученные коэффициенты в (2.9):

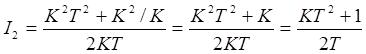
Найдем шумовую полосу:                                                    

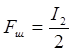                                                                                                          (2.12)

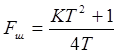, [Гц]                                                (2.12а)

Дисперсия шумовой ошибки:

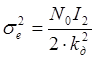   [Гц²]                                              (2.13)

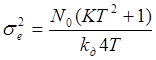                                              (2.14)

Подставим (2.2) и (2.14) в (2.5):

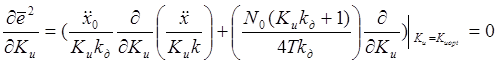                  (2.15)

Выполнив математические преобразования, получим:

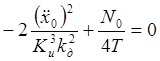                                                (2.16)

        

                                           

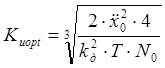
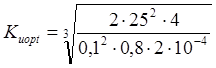
Зная величину K_иopt рассчитаем по формуле (2.12а) оптимальное значение шумовой полосы F_шoptсистемы и по формуле (2.1) минимально достижимую ошибку слежения e_min.

 

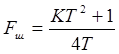
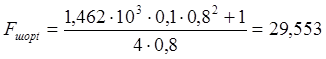,  Гц                                                                                                

   [Гц²]

                                   

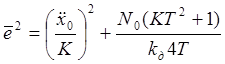
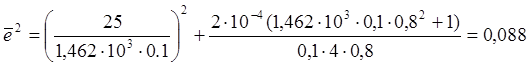
Для построения графика зависимости , установим связь между  и  через коэффициент К:

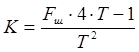,                                               (2.17)

Следовательно

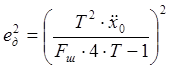   , [Гц²]                               (2.18)

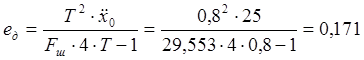 ,  [Гц]               (2.18а)

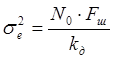                                                     (2.19)

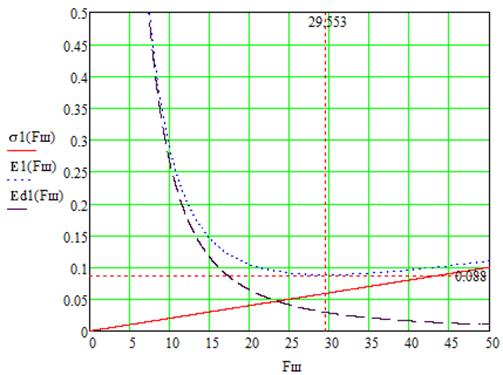
Рисунок 2. – График зависимости ошибок слежения от полосы про-                               пускания системы: –, –,  –.

При малых значениях F_ш  основной вклад в результирующую ошибку  вносит составляющая е_д , а при больших F_ш– шумовая составляющая е_n .

3. ЛАХ И ЛФХ СИСТЕМЫ

         Для определения запаса устойчивости системы построим логарифмическую амплитудную и фазовою характеристики, по которым установим запас по усилению и фазе.

Передаточная функция разомкнутой системы имеет вид (1.3):

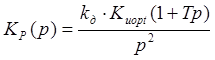,                                        (3.1)

где К_иopt=1,462*10³

k_д =0,1  В/Гц

T=0,8 c

Если проанализировать выражение (3.1) , то можно определить, что передаточная функция разомкнутой системы задается форсирующим звеном и двумя интеграторами.

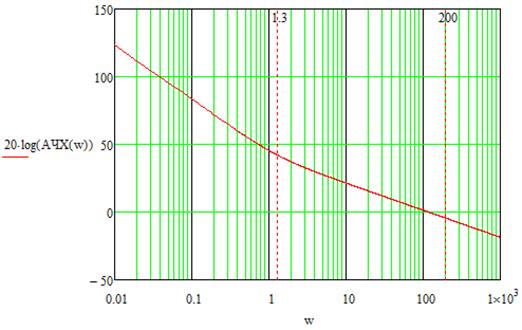
Рисунок 3. – ЛАХ системы (к определению запаса устойчивости).

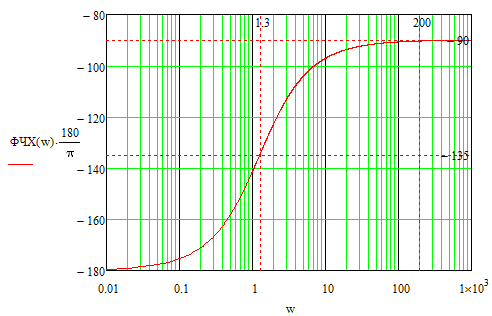
Рисунок 4. – ЛФХ системы (к определению запаса устойчивости).

 Запас по фазе определяется как:

                                        (3.2)

Из графиков (рисунок 3 и рисунок 4) видно, что запас по фазе составляет Δφ≈π/2.

Запас по амплитуде (усилению) численно равен значению ЛАХ на критической частоте (частоте, на которой ЛФХ равна –π рад).

В нашем случае, запас по усилению (ΔL) не имеет смысла определять (теоретически он бесконечен, поскольку ЛФХ достигает  –π  рад лишь  в асимптотической точке ω → 0). Считаем, что система является устойчивой (так как полученные