Следящий измеритель дальности доплеровской спутниковой РНС. Оптимизация системы

порядок дифференциального уравнения, описывающего систему.

Определим передаточную функцию динамического звена по 1 и используя данные

k=2,  n=2, m=1 :

Передаточная функция разомкнутой системы определяется 3:

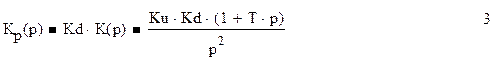
При анализе замкнутой системы полагаем, что помеха отсутствует. Тогда схема будет выглядеть:

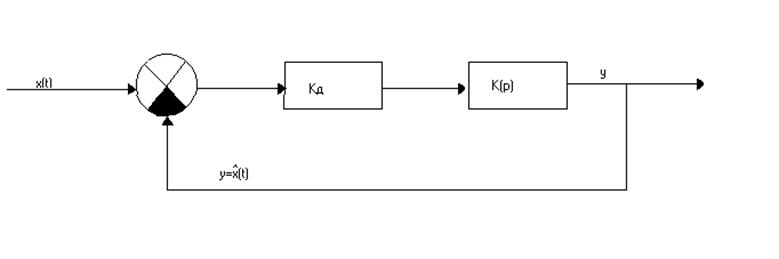
Рис.2.

Используя правила преобразования для последовательного и встречно – параллельного звеньев выведем передаточную функцию замкнутой системы:

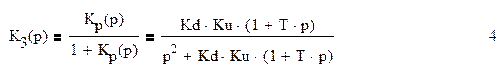
Для определения спектральной плотности эквивалентных флуктуаций, приведённых ко входу дискриминатора используем правило переноса сумматора с выхода на вход звена и вычислим по формуле 5:

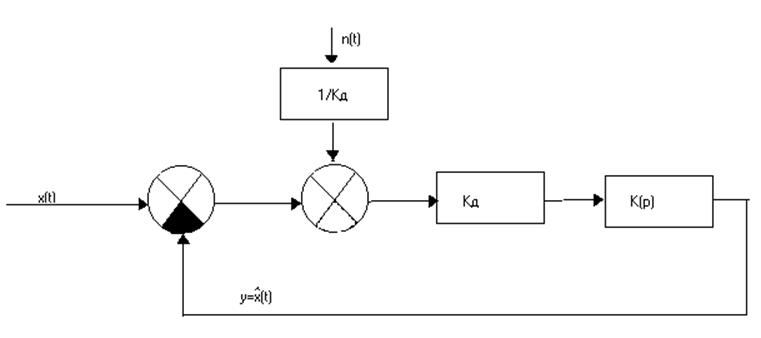
Найдём спектральную плотность эквивалентных флуктуаций:

2.Оптимизация параметров системы

Оптимизация системы по критериюминимума среднего квадрата ошибки сводится к нахождению значения параметра Кu, при котором обеспечивается минимум величины:

                                              5а где - динамическая ошибка, определяемая инерционностью системы;

- дисперсия шумовой ошибки, определяемая помехой n(t).

Порядок астатизма рассматриваемой системы равен 2, поэтому динамическая ошибка

определяется параметром (в дальнейшем будем обозначать ) задающего воздействия 6:

где  =

Реальный шум имеет ограниченную ширину спектра, однако она во много раз превышает полосу пропускания системы, что позволяет в качестве шума использовать модель белого шума. Дисперсия шумовой ошибки определяется по формуле 7:

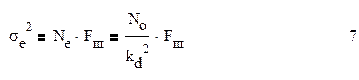
где

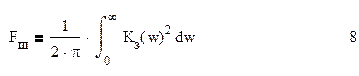
Формула 8 определяет шумовую полосу следящей системы.

- АЧХ замкнутой системы.

Передаточная функция звена, определяющего динамические свойства системы, имеет вид:

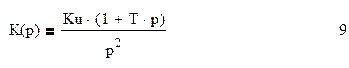
Тогда передаточная функция замкнутой системы, имеет вид:

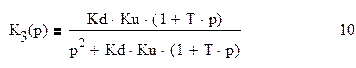
Заменив параметр p на jw, получаем выражение для комплексного коэффициента передачи замкнутой системы:

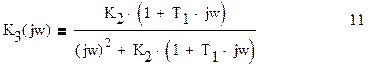
Для квадрата модуля комплексного коэффициента передачи(квадрат АЧХ системы) запишем:

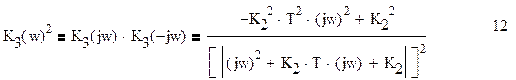
Сравнивая выражения 12 и 13, получаем для коэффициентов полиномов:

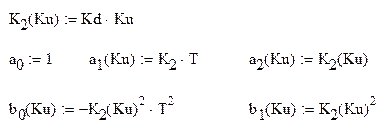
Значение интеграла 8,при n=2 вычислим исходя из значения коэффициентов полиномов:

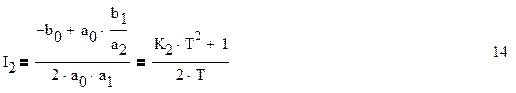
Тогда шумовая полоса системы  и дисперсия шумовой ошибки:

Динамическая ошибка определяется параметрами и  задающего воздействия, а также  порядком астатизма системы и добротностью . В нашем случае порядок равен 2, поэтому можно записать:

Для нахождения оптимального значения параметра Кu продифференцируем выражение

5а для среднего квадрата ошибки и при равняем её к нулю:

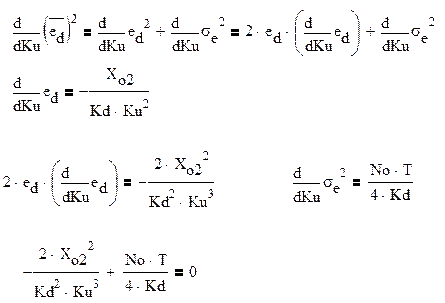
Выражаем Ku:

 

 

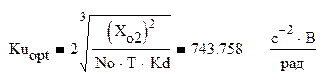
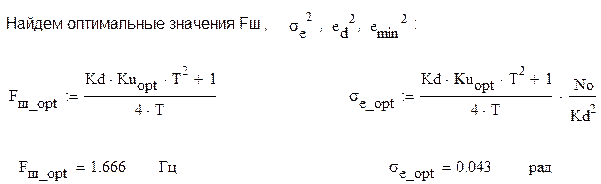
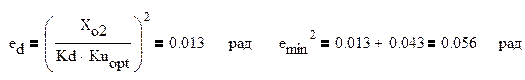
Зависимости ошибок слежения от полосы пропускания системы выражаются ниже приведёнными формулами, а график приведен на рис.3:

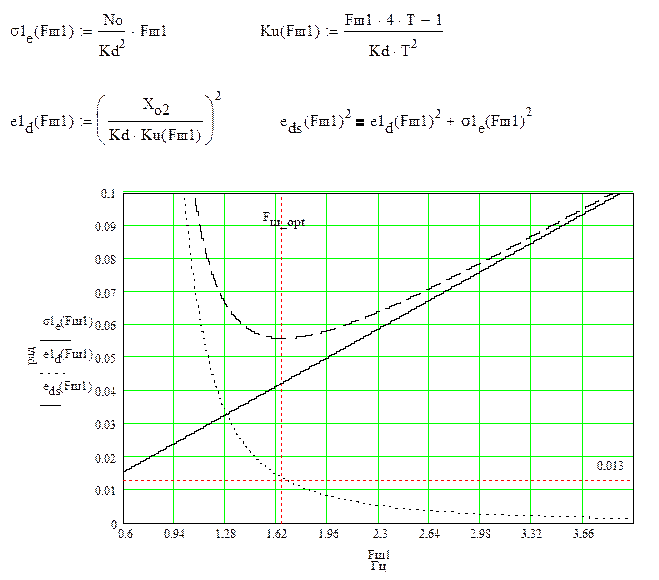
                            Рис.3. Графики функций ошибок слежения.

Физический смысл существования оптимального значения полосы Fш объясняется              следующим образом. При малых значениях Fш основной вклад в результирующую ошибку вносит , а при больших Fш - шумовая составляющая еn рис.3. Поэтому                     существует оптимальное значение шумовой полосы Fш opt, при котором результирующая      ошибка минимальна.

3. Определение запасов устойчивости системы.

Для определения АЧХ и ФЧХ разомкнутой системы представим динамическое звено в виде последовательно соединенных двух интегрирующих и одного форсирующего звеньев.

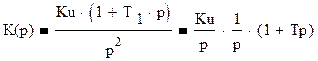
ЛАХ будет определяться суммой логарифмических АЧХ и ФЧХ отдельных звеньев.

ЛАХ интегрирующих звеньев определяется как:

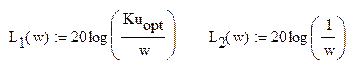
ЛАХ форсирующего звена:

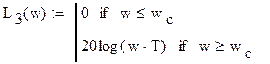
где частота сопряжения.

Следовательно, суммарная:

ЛФХ звена:

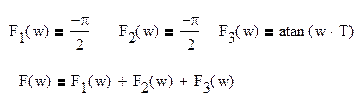
Графики приведены на рис.4:

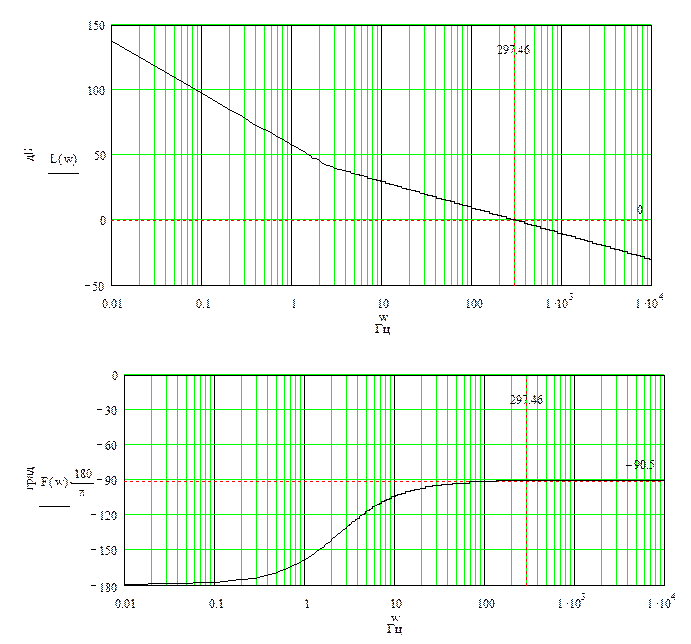
Рис.4. ЛАХ и ЛФХ системы.

ЛАХ пересекает ось абсцисс с наклоном -20 дБ, значит, перерегулирование