Система слежения за задержкой (ССЗ). Основные параметры системы, передаточные функции

Министерство образования Российской Федерации

Красноярский Государственный

Технический Университет

Кафедра Радиосистем

КУРСОВАЯ РАБОТА

СИСТЕМА СЛЕЖЕНИЯ ЗА ЗАДЕРЖКОЙ

Пояснительная записка

Выполнил:

Студент группы Р28-1

Проверил:

Преподаватель

Красноярск

2001г.

ЗАДАНИЕ

по курсовому проектированию

1. Тема курсовой работы:               Система слежения за задержкой (ССЗ)

2. Срок сдачи законченной работы:                 15.05.01 г.                      

3. Исходные данные к работе:

а) Номер варианта:– №6

б) Параметры задающего воздействия - , ;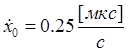

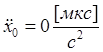в) Спектральная плотность шума - ;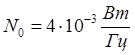

г) Коэффициент передачи дискриминатора - ;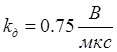

д) Параметры динамического звена: , , , .

е) Область применения – цифровой следящий измеритель дальности некогерентной импульсной РЛС (сложный ЛЧМ сигнал).

4. Содержание расчетно–пояснительной записки:

1) Передаточные функции разомкнутой и замкнутой системы.2

2) Оптимизация следящей системы.3

3) Построение ЛАХ, ЛФХ и определение запаса устойчивости.7

4) Цифровое моделирование системы.12

5) Составление функциональной схемы.15

Список используемых сокращений.17

Вывод.18

Список используемой литературы.20

1.Передаточные функции разомкнутой и замкнутой системы.

Имеется структурная схема следящей системы рис.1.

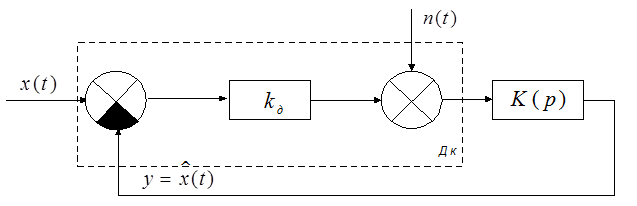
Рис.1 Структурная схема следящей системы

Передаточная функция звена будет равна: .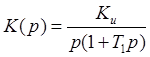

Тогда передаточная функция разомкнутой системы: .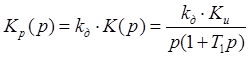

Передаточная функция замкнутой системы: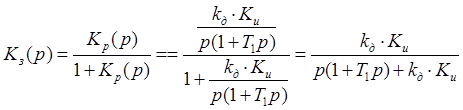

.Для того чтобы определить спектральную плотность эквивалентных флуктуаций, приведенных ко входу дискриминатора воспользуемся правилом преобразования структурных схем (перенос сумматора с выхода на вход звена).

Получим преобразованную структурную схему рис.2.

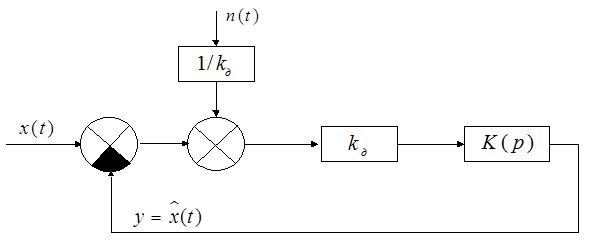
Рис.2 Преобразованная структурная схема следящей системы.

Тогда спектральная плотность эквивалентного шума будет равна: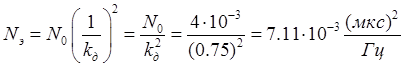

2. Оптимизация следящей системы.

Передаточная функция звена, определяющего динамические свойства системы, имеет вид: .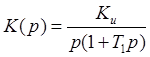

Передаточная функция замкнутой системы:

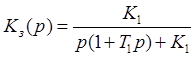, где  - добротность системы по скорости.

Проведем оптимизацию системы по критерию минимума среднего квадрата ошибки. Найдем такое значение параметра , при котором обеспечивается минимум величины . Составляющая  определяет динамическую ошибку, обусловленную инерционностью системы, а составляющая  определяет дисперсию шумовой ошибки, обусловленной помехой .

Динамическая ошибка  определяется параметрами  и  задающего воздействия, а так же порядком астатизма и добротностью  системы.

В нашем случае, для рассматриваемой системы 1-го порядка, порядок астатизма равен 1 (к=1), тогда динамическая ошибка определяется как: 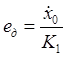, где ₁ с ' - добротность системы по скорости.

Случайная составляющая ошибки определяется статистическими характеристиками помехи  и структурой (параметрами) системы. Так как мы будем использовать в качестве  модель белого шума с равномерной спектральной плотностью в полосе частот от 0 до ¥, тогда дисперсию шумовой ошибки можно рассчитать по формул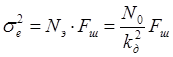е:, где 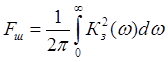 -  шумовая полоса

 следящей системы в Гц,,  - АЧХ замкнутой системы.

Определим шумовую полосу рассматриваемой системы.

Передаточная функция замкнутой системы:;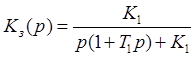

Заменим в формуле параметр , получим выражение для комплексного коэффициента передачи замкнутой системы:,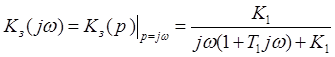

Тогда для квадрата модуля комплексного коэффициента передачи (квадрат АЧХ) запишем: .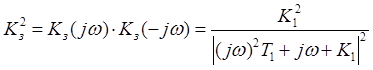

Вычисление интеграла шумовой полосы упрощается, если представить подынтегральное выражение в виде:

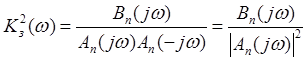, где полиномы

,

,

n – порядок дифференциального уравнения, описывающего систему.

Для исследуемой системы n=2,тогда

Приравнивая соответствующие коэффициенты, находим:

  

 

Тогда нахождение шумовой полосы системы и дисперсии шумовой ошибки сводится к вычислению интеграла 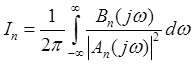, т.к. у нас n=2, тогда получим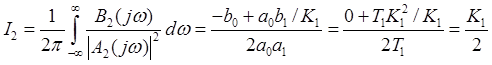

Шумовая полоса системы: ,

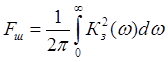Дисперсия шумовой ошибки: .

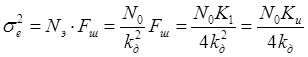Произведем оптимизацию системы.

Для нахождения экстремума среднего квадрата ошибки, продифференцируем выражение для среднего квадрата ошибки по параметру  и приравняем производную нулю:

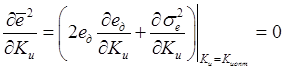, где: , , ,

.

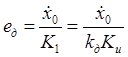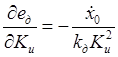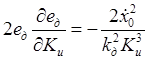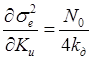Подставляя эти значения, получим уравнение:

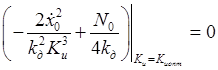
Откуда выражаем оптимальное значение параметра :

,       , .

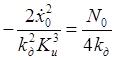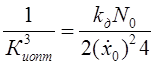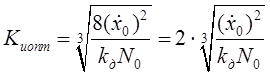Подставляя численные значения, получим:

.

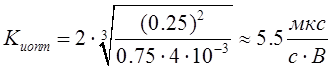Найдем оптимальные значения шумовой полосы следящей системы, а так же дисперсию шумовой ошибки и динамическую ошибку, при :

,

,

;  .

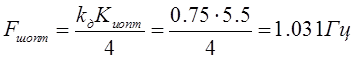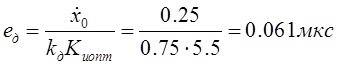Найдем значение минимально достижимой ошибки слежения:

,

.

Физический смысл существования оптимального значения полосы  можно объяснить так. При малых значениях  основной вклад в результирующую ошибку  вносит составляющая , а при больших  - шумовая составляющая . Поэтому существует оптимальное значение шумовой полосы , при котором результирующая ошибка минимальна.

Это можно увидеть из графиков зависимости ошибок слежения от полосы пропускания системы:

; ; .

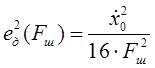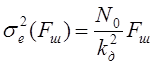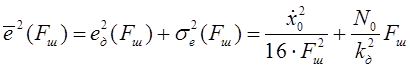Графики этих функций приведены на Рис. 1:

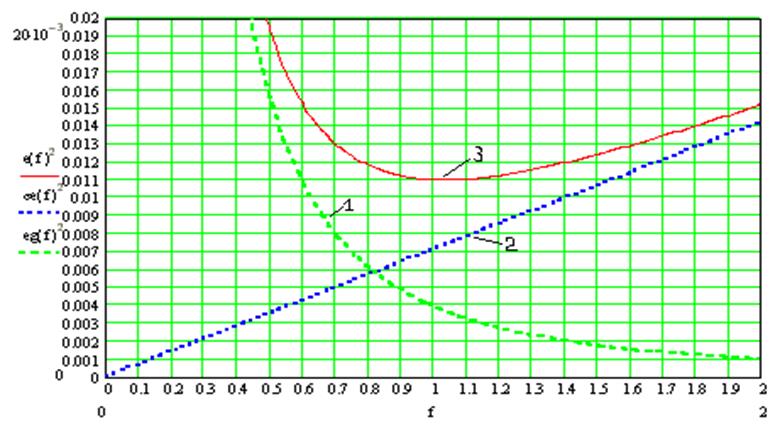
Рис.3. График зависимости ошибок слежения от полосы пропускания системы:

1 -- ;   2 -- ;   3 -- .

3. Определение запасов устойчивости следящей системы.

Определим запас устойчивости системы, используя метод логарифмических частотных характеристик, суть которого сводится к построению ЛАХ и ЛФХ разомкнутой следящей системы.

Так как передаточная функция разомкнутой следящей системы равна