 Системы СДЦ на базе
автокомпенсаторов, известные под названием череспериодные автокомпенсаторы
(ЧПАК), являются разновидностью систем СДЦ с внешней когерентностью. Режекция
спектральных составляющих сигналов пассивных помех в таких системах может
осуществляться как на видеочастоте, так и на радиочастоте. Причем переход на
радиочастоту, в отличие от обычных систем СДЦ, не сопровождается резким
повышением требований к стабильности УЛЗ. Кроме того, подобные системы СДЦ
могут не иметь устройства формирования опорного напряжения.
Системы СДЦ на базе
автокомпенсаторов, известные под названием череспериодные автокомпенсаторы
(ЧПАК), являются разновидностью систем СДЦ с внешней когерентностью. Режекция
спектральных составляющих сигналов пассивных помех в таких системах может
осуществляться как на видеочастоте, так и на радиочастоте. Причем переход на
радиочастоту, в отличие от обычных систем СДЦ, не сопровождается резким
повышением требований к стабильности УЛЗ. Кроме того, подобные системы СДЦ
могут не иметь устройства формирования опорного напряжения.
а)
б)
Рис.4.62. Структурные схемы одноканальной и двухканальной ЧПАК на радиочастоте
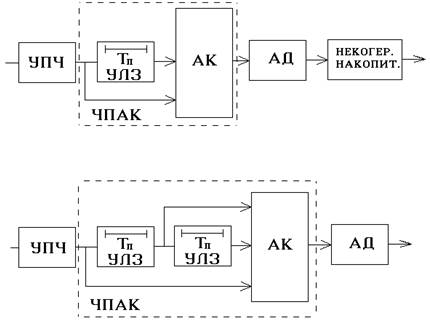
На рис.4.62 представлены структурные схемы одноканальной и двухканальной ЧПАК на радиочастоте.
Понятие кратности вычитания ЧПК для ЧПАК трансформируется в понятие канальности, т.е. числа дополнительных каналов (линий задержки на Тп). Рабочая частота УЛЗ в данном случае равна промежуточной частоте (ПЧ), поэтому отпадает необходимость использования модулирующего гетеродина и модулятора для обеспечения нормальной работы УЛЗ.
Одним из основных элементов ЧПАК является автокомпенсатор. Он представляет собой самонастраивающееся устройство с корреляционными обратными связями, обеспечивающее исключение из спектра сигналов помех в основном канале АК составляющих, коррелированных с сигналами помех в дополнительных каналах АК. Основным каналом АК принято называть канал, в котором отсутствует усилитель с регулируемым коэффициентом передачи, а дополнительные - каналы с регулируемыми коэффициентами передачи.
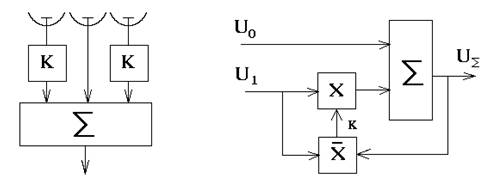
Рис.4.63 Рис.4.64
Подбор коэффициентов в многоканальных схемах (подобных схеме, показанной на рис.4.63) можно осуществить используя принцип корреляционной обратной связи. На рис.4.64 показана схема с двумя входами, на которые поступают напряжения одной и той же частоты с комплексными амплитудами Uo(t) и U1(t).
На сумматоре образуется напряжение Us(t) = Uo(t) + kU1(t).
Имеется цепь обратной связи, в которую включено устройство вычисления оценки корреляционного момента Us(t)U1*(t).
Последний с точностью до постоянной æ используется в качестве управляющего множителя k, подаваемого на управляющий элемент. Из двух уравнений
k = Us(t)U1*(t),
Us(t) = Uo(t) + kU1(t), где U1(t) = Uo(t-Тп), то можно найти
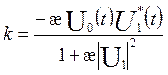
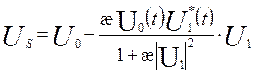 .
.
При æ → ∞ и достаточной корреляции напряжений Uоп и U1 (например, при U1=cUо) происходит полная компенсация, т.е. Us обращается в ноль
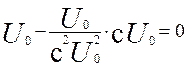 .
.
При этом k = - ρ(Тп) при одинаковой мощности помех в соседних периодах повторения. Усилитель с регулируемым коэффициентом передачи может быть реализован с помощью:
двух квадратурных каналов с регулируемыми: коэффициентами усиления и фазовым сдвигом между каналами π/2 радиан;
управляемого смесителя частоты.
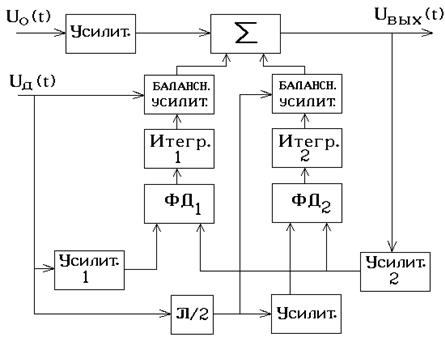
Рис.4.65. Структурная схема квадратурного АК
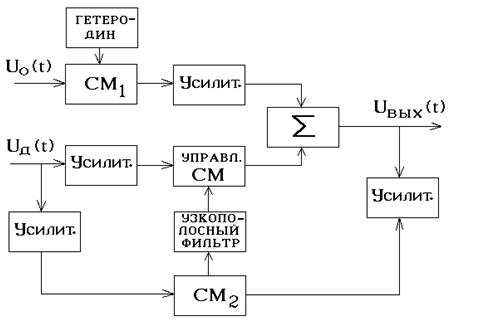
Рис.4.66. Структурная схема гетеродинного АК
В первом случае АК называется квадратурным, а во втором - гетеродинным ( см. рис.4.65 и 4.66 соответственно).
Роль корреляторов в квадратурном АК выполняют ФД и интеграторы (чаще всего на базе операционных усилителей), а в гетеродинных - смеситель 2 и узкополосный фильтр.
Балансные усилители (БУ) в квадратурных АК помимо изменения амплитуды входных сигналов дополнительных каналов обеспечивают их прохождение к сумматору либо без изменения фазы, либо с изменением ее на π радиан. Значение фазового сдвига (0 или π радиан) определяется полярностью напряжения на выходе ФД.
Таким образом, как следует из рис.4.65 и 4.66, потенциальные возможности обоих типов АК одинаковы и целесообразность использования того или иного типа определяется лишь требованием упрощения аппаратурной реализации. При использовании интегральных микросхем преимущество в этом отношении имеет квадратурный АК.
ЧПАК представляет собой систему СДЦ с адаптивным режекторным фильтром. Положение провалов в АЧХ ЧПАК автоматически изменяется таким образом, чтобы обеспечить режекцию спектральных составляющих сигналов ПП. Покажем это на примере одноканального ЧПАК, эквивалентная схема которого приведена на рис.4.67,а.
В соответствии с определением частотная характеристика определяется соотношением:
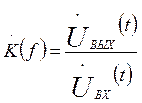
Для данного устройства при ![]() (t) =
exp [ jωt] :
(t) =
exp [ jωt] :
ִ ִ
Uвых(t) = exp [ jωt] + K.exp [ jω(t-Tп)], тогда
ִ ִ ִ
K(f) = 1 + K.exp [ -jωTп] = 1 - ρ(Тп).exp [ -jωTп].
Коэффициент междупериодной корреляции сигналов ПП ρ(Тп) можно представить в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.