









Федеральное агентство по образованию
Государственное общеобразовательное учреждение
высшего профессионального образования
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра Радиосистем
Курсовая работа.
Следящая система АПЧ
Вариант 17
Выполнил:
Ст-т. гр. Р55-4
Проверил:
Красноярск 2008
Содержание:
Вывод______________________________________________________________________ 11
Литература__________________________________________________________________ 12
1. Исходные данные:
Тип следящей системы – АПЧ
Параметры задающего воздействия: х0 = 1,25 Гц/с
х0 = 0
Коэффициент передачи дискриминатора – kд = 0,16 В/Гц
Спектральная плотность шума – N0 = 4×10-4 Вт/Гц
Параметры динамического звена:
Число интеграторов – k = 1
Порядок дифференциального уравнения, описывающего систему – n = 3
Число форсирующего звена – m = 0
Число инерционных звеньев – n-k = 2
Постоянные времени инерционных звеньев: Т1 = 0,14 с
Т2 = 0,02 с
Область применения системы – демодулятор ЧМ сигнала.
Передаточная функция: K(p) =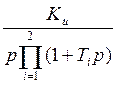
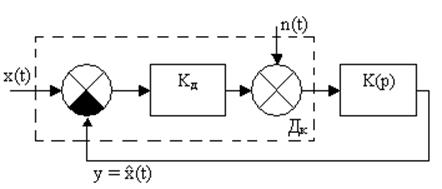 |
Рис.1 Структурная схема следящей системы.
2. Определение передаточных функций, спектральной плотности эквивалентных флуктуаций, приведённых ко входу дискриминатора
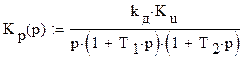 |
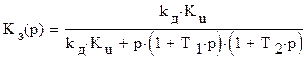 |
|||
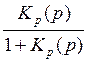
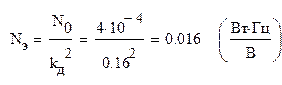 |
|||
3. Оптимизация следящей системы
Оптимизацию проведём по критерию минимума среднего квадрата ошибки. Критерий сводится к нахождению значения параметра Ku, при котором обеспечивается минимум величины ē2 = ед2 + σе2
Составляющая ед определяет динамическую ошибку, обусловленную инерционностью следящей системы по отношению к меняющемуся задающему воздействию. Составляющая σе2 определяет дисперсию шумовой ошибки еn(t), обусловленной помехой n(t).
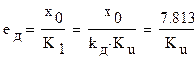 |
|||
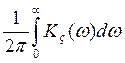
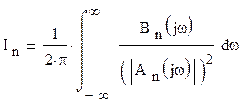 |
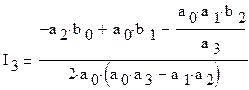 |
|||
где a0, a1, a2, a3, b0, b1, b2 – коэффициенты соответствующих полиномов An(jω) и Bn(jω).
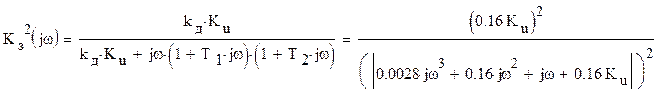 |
Коэффициенты соответственно будут:
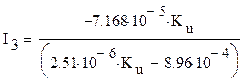 |
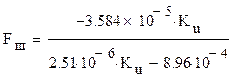 |
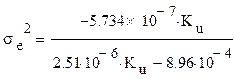 |
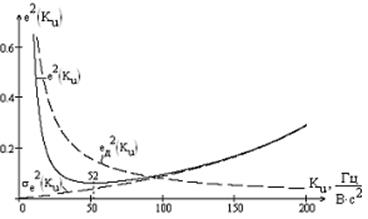 |
Рис.2 Зависимость квадрата ошибки от Ku
Оптимальное значение Ku = 52
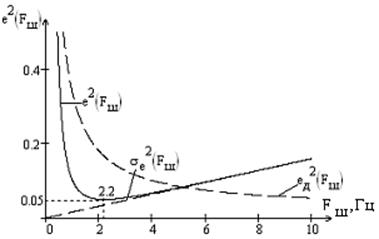 |
Рис.3 Зависимость квадрата ошибки от Fш
Оптимальное значение шумовой полосы Fш = 2,2
Минимально достижимая ошибка слежения еmin = 0,05
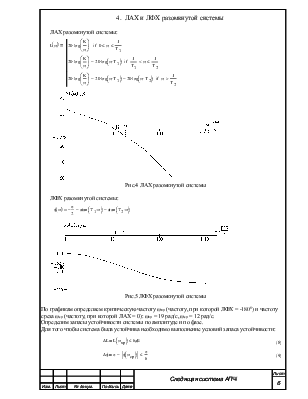
4. ЛАХ и ЛФХ разомкнутой системы
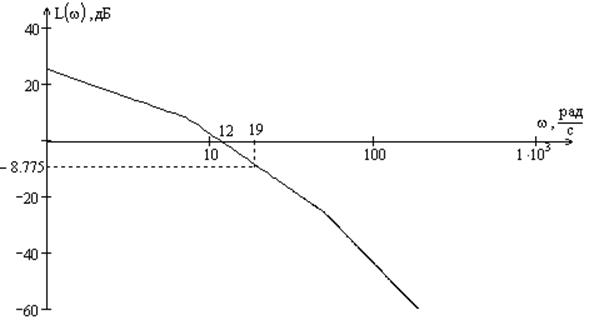 |
Рис.4
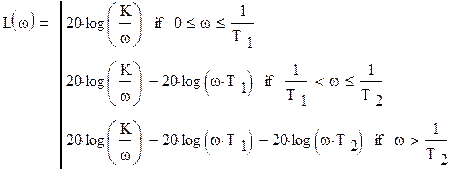 |
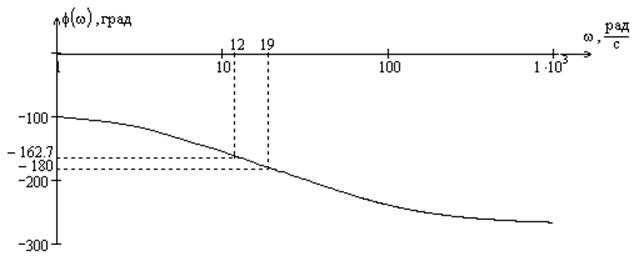 |
Рис.5 ЛФХ разомкнутой системы
По графикам определяем критическую частоту ωкр (частоту, при которой ЛФХ = -1800) и частоту среза ωср (частоту, при которой ЛАХ = 0): ωкр = 19 рад/с, ωср = 12 рад/с.
Определим запасы устойчивости системы по амплитуде и по фазе.
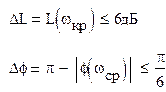 |
|||
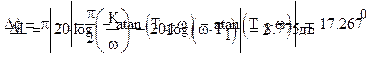 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.