Задание по курсовому проектированию на тему "Система ССЗ"

СОДЕРЖАНИЕ

Задание по курсовому проектированию........................................................................ 3

1. Задание 1...................................................................................................................... 3
2. Задание 2...................................................................................................................... 4
3. Задание 3...................................................................................................................... 7
4. Задание 4...................................................................................................................... 8
5. Задание 5.................................................................................................................... 11

Литература...................................................................................................................... 12

ЗАДАНИЕ ПО КУРСОВОМУ ПРОЕКТИРОВАНИЮ

Тема курсовой работы: ......................................................................  система ССЗ

Исходные данные к работе:

Параметры задающего воздействия .......................................... ,

Спектральная плотность шума.................................................... N₀=8∙10^-4 Вт/Гц

Параметры системы....................................................................... k_д=0.25 В/мкс, k=2, n=2, m=1, T₁=0.05 с

Область применения...................................................................... следящий измеритель дальности спутниковой РНС

(сложный ФМ-сигнал)

Содержание расчетно-пояснительной записки (перечень подлежащих разработке вопросов)

а) Оптимизация системы;

б) Построение ЛАХ, ЛФХ и определение запасов устойчивости;

в) Цифровое моделирование системы;

г) Составление функциональной схемы.

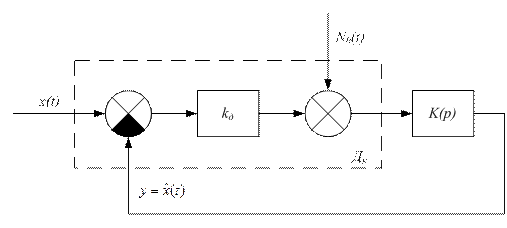
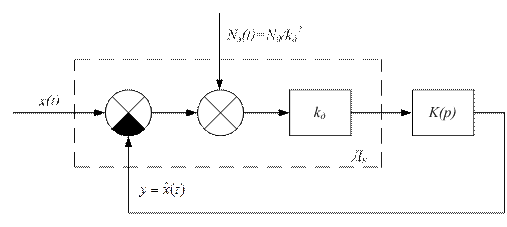
Рисунок 1 – Структурная схема следящей системы

ЗАДАНИЕ 1

• Определение передаточных функций разомкнутой и замкнутой систем;
• Определение спектральной плотности эквивалентных флуктуаций, приведенных ко входу дискриминатора.

Передаточная функция динамического звена:

 

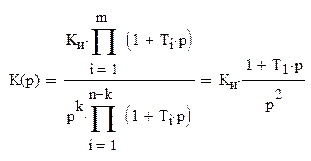
Передаточная функция разомкнутой системы:

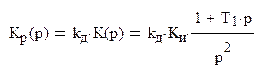
Передаточная функция замкнутой системы:

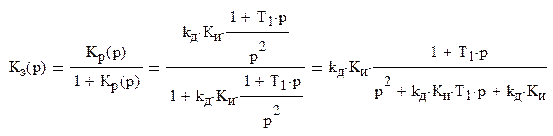
Спектральная плотность эквивалентных флуктуаций, приведенных ко входу дискриминатора:

                    

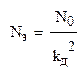
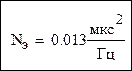
ЗАДАНИЕ 2

• Оптимизация следящей системы по параметру К_и, используя критерий минимума среднего квадрата ошибки;
• Определение оптимального значения шумовой полосы F_ш системы и минимально достижимую ошибку слежения e_min;
• Построить графики зависимостей результирующей средней квадратической ошибки слежения, а также ее составляющих (динамической и шумовой) от полосы.

Критерий минимума среднего квадрата ошибки:

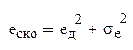
Динамическая ошибка для системы 2-го порядка астатизма и квадратичного воздействия:

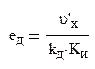
Шумовая полоса замкнутой АС:

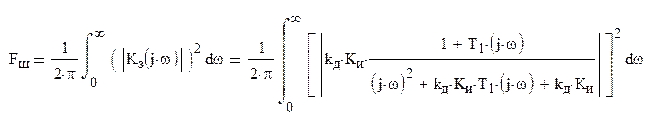
Дисперсия ошибки, обусловленная помехой:

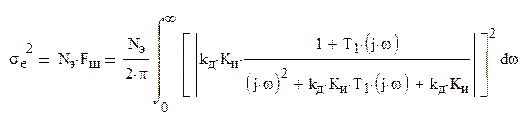
Критерий минимума среднего квадрата ошибки как функция от К_и:

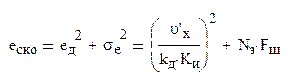
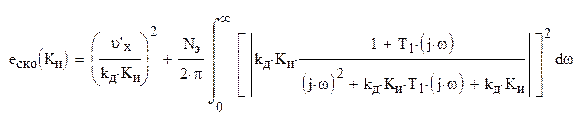
Оптимальный параметр системы в виде коэффициента передачи К_и:

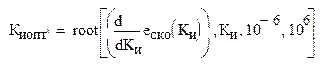
Но, для обеспечения адекватного запаса по усилению и фазе в дальнейшем, необходимо как минимум:

Оптимальная шумовая полоса замкнутой АС:

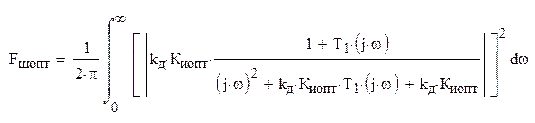
Минимально достижимая ошибка слежения:

 

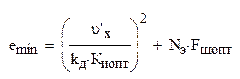
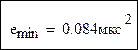
Определяем зависимость динамической ошибки от шумовой полосы, возвращаясь к интегралу F_ш:

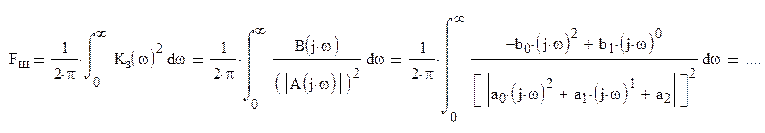
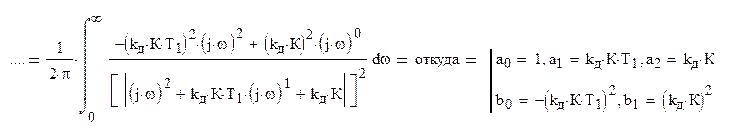
Данный интеграл при n=2 имеет решение в виде:

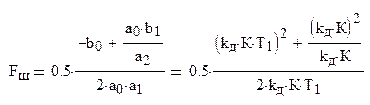
Откуда добротность системы по ускорению как функция шумовой полосы:

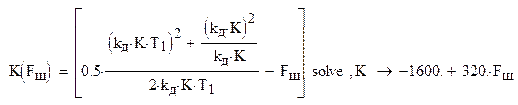
Динамическая ошибка и дисперсия ошибки как функции шумовой полосы:

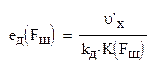
Средний квадрат ошибки как функция шумовой полосы:

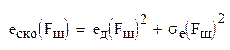
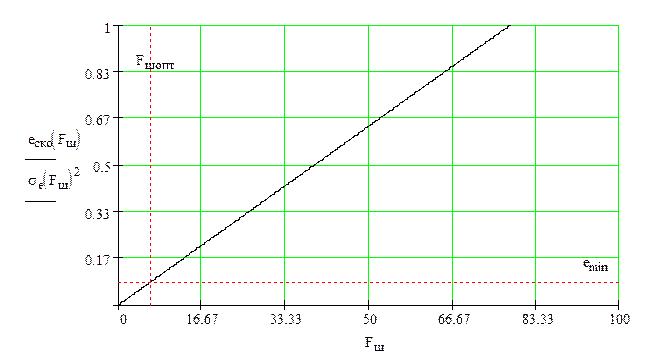
Рисунок 2 – Средний квадрат ошибки как функция шумовой полосы

ЗАДАНИЕ 3

Построить логарифмическую амплитудно-частотную (ЛАХ) и фазо-частотную (ЛФХ) характеристики разомкнутой системы и определить по ним запас устойчивости по амплитуде и фазе при оптимальном значении параметра К_и.

Амплитудно-частотная характеристика разомкнутой системы:

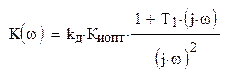
Частоты среза и сопряжения соответственно:

                  

    

 

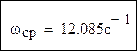
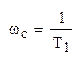
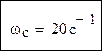
Логарифмическая амплитудно-частотная характеристика (ЛАХ) разомкнутой системы:

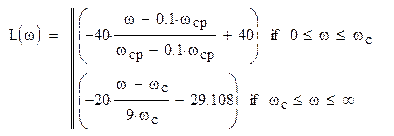
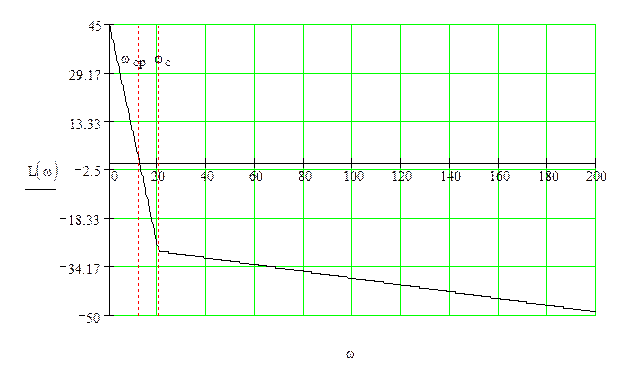
Рисунок 3 – Асимптотическая ЛАХ разомкнутой системы

Фазо-частотная характеристика разомкнутой системы:

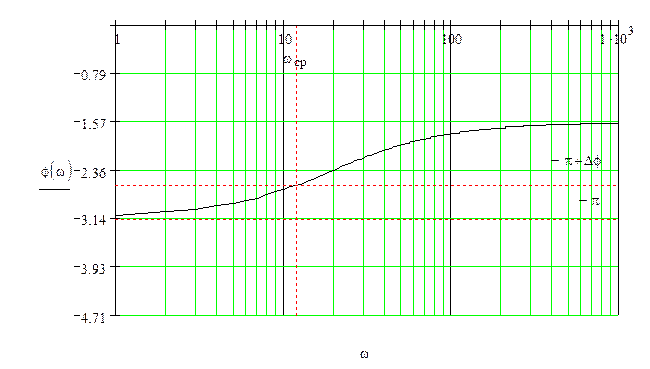
Рисунок 4 – ЛФХ разомкнутой системы

Запасы по усилению (асимптотически) и фазе соответственно:

                                       

                         

ЗАДАНИЕ 4

• Произвести моделирование следящей системы на ЭВМ при двух типах воздействия: а) ступенчатом; б) линейном или квадратичном (в соответствии с вариантом задания);
• Построить графики переходного процесса и определить качественные показатели системы в переходном режиме.

Интервал дискретизации, выбираемый из условия T<<1/(2F_ш):

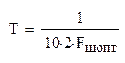
Дискретная передаточная функция для ошибки в цифровой модели следящей системы:

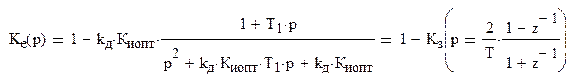
Для облегчения восприятия и проведения операций заменим z^-1 на z и выполним преобразования:

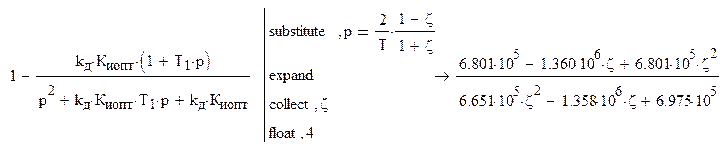
Коэффициент передачи представляем в виде дробно-рациональной функции с учетом замены z^-1=z:

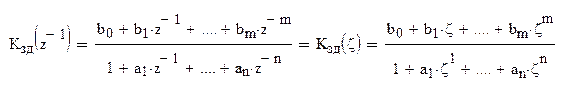
Для придания нужного вида дроби делим числитель и знаменатель на 697503.44853323701620 и определяем коэффициенты a=[a₀, a₁, a₂], b=[b₀, b₁, b₂] относительно z:

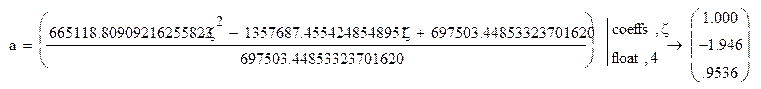
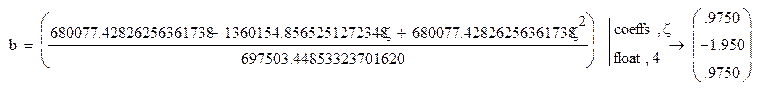
Ступенчатое и квадратичное воздействия соответственно:

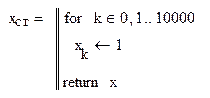
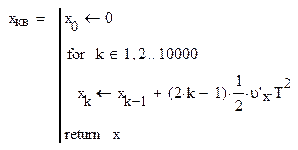
Блок вычисления разностного уравнения относительно ошибки слежения:

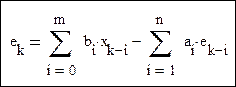
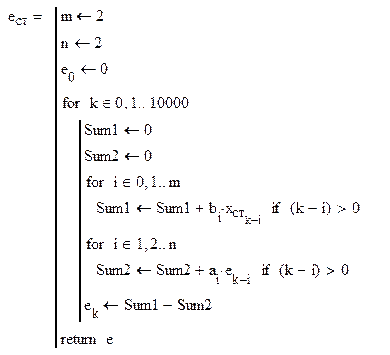
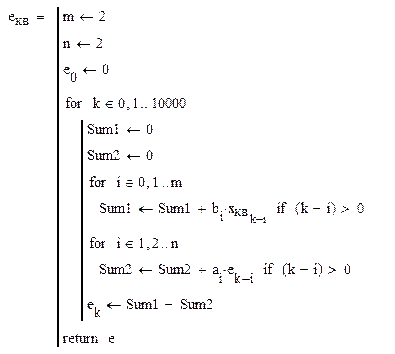
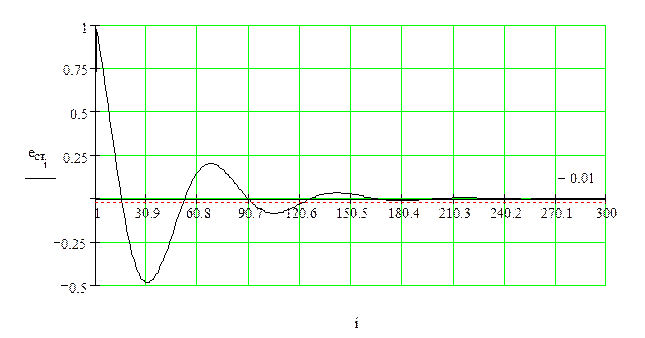
Рисунок 5 – Переходный процесс относительно ошибки – ступенчатое