Качество систем автоматического управления, страница 4

В устойчивой системе в установившемся режиме (t = ∞) производные всех порядков равны нулю; следовательно, из (1.12.25) имеем

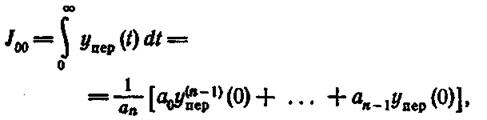                 (1.12.26)

т. е. линейная интегральная оценка J₀₀ определяется коэффициентами дифференциального уравнения системы и начальными условиями.

Если принять за идеальный переходный процесс скачкообразный переход, протекающий мгновенно и без перерегулирования, то стремление J₀₀ к нулю будет соответствовать стремлению к идеальному переходному процессу (см. рисунок 1.12.З.б.). Однако если заранее неизвестен вид переходного процесса, то использование линейной интегральной оценки J₀₀ может привести к неверным выводам, ибо при сильном перерегулировании (см. рисунок 1.12.З.a) J₀₀→ 0, но это вовсе не означает качественности переходного процесса.

Квадратичные интегральные оценки.

Это оценки вида

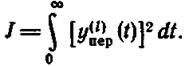                                      (1.12.27)

Простейшая квадратичная оценка

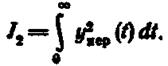                                         (1.12.27.а)

Подобные оценки свободны от недостатков, свойственных линейным оценкам. Чем меньше будет сумма абсолютных величин площадей между y²_ПЕР(t) и осью времени, тем меньше будет величина J₂. Следовательно, они применимы и к колебательным системам.

Вычисление J₂ может быть произведено различными способами. Остановимся на одном из них, предложенном академиком Л. И. Мандельштамом. Разберем этот способ на примере уравнения 3-го порядка

               (1.12.28)

где для краткости у = y_ПЕР, а количество штрихов обозначает степень производной. По аналогии этот метод легко обобщить на уравнение n-й степени. Умножим все члены уравнения (1.12.28) на величину y"(t) и проинтегрируем полученное уравнение в пределах от 0 до ∞:

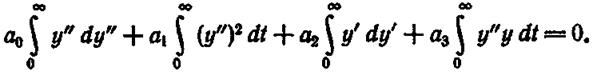
Из устойчивости системы следует, что все производные при t = 0 равны 0. Вводя обозначения

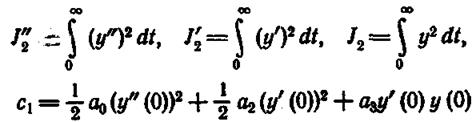
и учитывая, что уу" = (уу')' — (У')². получим a₁J"₂ — a₃J'₂ = c₁. Умножая (1.12.28) на у', а затем на у, и производя аналогичные действия, имеем еще два уравнения:

где

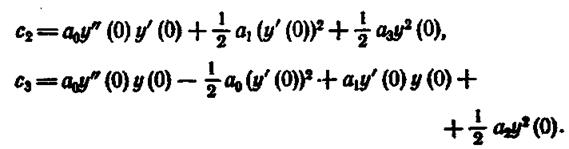
Таким образом, для определения J₂ имеем систему трех алгебраических уравнений с тремя неизвестными J₂", J₂', J₂ откуда по правилу Крамера находим J₂ = Δ₁/ Δ, где

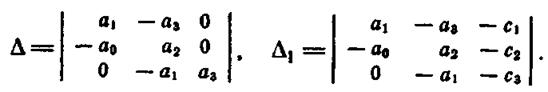
Оценка J₂ хотя и свободна от недостатков оценки J₀₀, однако не дает никакой информации о степени колебательности переходного процесса. Поэтому вполне возможна ситуация, что оценка J₂ будет меньше при сильно колебательном переходном процессе, в то время как менее колебательный и более практически пригодный переходный процесс будет иметь большее значение J₂.

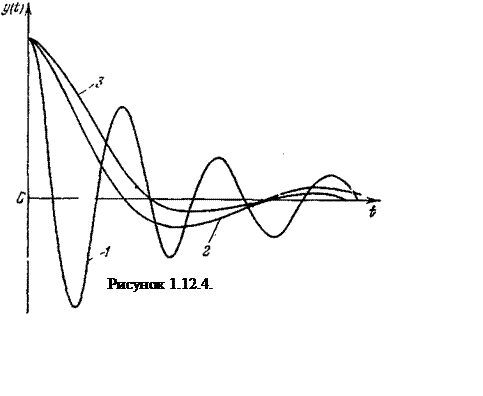
На рисунке 1.12.4. показаны три различных процесса, соответствующих одному и тому же значению интегральной квадратичной оценки J₂. Видно, что процесс 1 мало пригоден для практики, процесс 2 - удовлетворителен, а процесс 3 - соответствует хорошему качеству системы.

От перечисленных выше недостатков свободна оценка, которая, помимо y²_ПЕР учитывает и (y_ПЕР/dt) - квадрат скорости протекания процесса. Запишем ее в виде

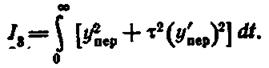                                  (1.12.29)

Этот интеграл можно преобразовать:

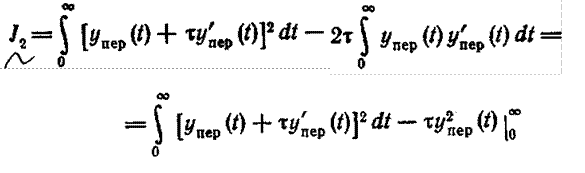
Так как y_ПЕР (∞) = 0, то окончательно получаем

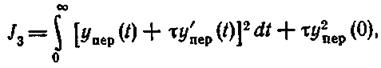                         (1.12.30)

откуда следует, что при заданной постоянной τ рассматриваемый интеграл J₃ имеет минимум, если

                                      (1.12.31)

т. е. если переходный процесс имеет вид экспоненты:

Оценку качества системы по минимуму интеграла J₃ обычно производят только в тех случаях, когда можно, исходя из требований, с одной стороны, плавности переходного процесса регулирования, а с другой стороны - быстродействия, указать примерное значение показателя τ оптимальной экспоненты. Обычно задают τ в пределах t_ПЕР/6<τ<t_ПЕР/3, где t_ПЕР — требуемое время установления (регулирования).