Качество систем автоматического управления, страница 2

Оценкой качества САУ в установившемся режиме обычно служит вынужденная составляющая ошибки

                                     (1.12.6)

Широко принято использовать для этих целей также среднеквадратичную ошибку

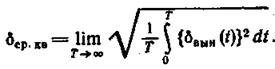                       (1.12.7)

1.12.2. Прямые методы определения показателей качества

В случае если удается найти аналитическое выражение для переходного процесса и построить график или экспериментально зафиксировать его, то не составляет труда оценить непосредственно исследуемый процесс по вышеприведенным показателям качества. Методы, позволяющие произвести подобную операцию, называются прямыми методами определения показателей качества.

Один из этих методов излагается в приложении П4.6, где говорится о методе решения неоднородных дифференциальных уравнений с постоянными коэффициентами при помощи методов операционного исчисления. Перечислим другие прямые методы определения показателей качества. К ним относятся:

а) методы, основанные на применении современной вычислительной техники;

б) частотные методы, основанные на обратном преобразовании Фурье.

Опишем более подробно каждый из этих методов.

Метод, основанный на использовании операционного исчисления. В (см. материалы соответствующей лекции и п. П.4.4.2. - «Переходная функция») показано, что переходный процесс в САУ, описываемой линейным дифференциальным уравнением с постоянными коэффициентами, может быть вычислен по формуле

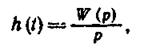                                             (1.12.8)

в которой для обратного преобразования Лапласа необходимо знать корни p_j (j = 1, 2, ..., n) характеристического уравнения

                                                      (1.12.9)

Следовательно, суть вопроса при использовании этого метода состоит в практическом умении определять корни характеристического уравнения системы, имеющей любой достаточно высокий порядок. Алгоритмы решения такой задачи реализованы практически на всех современных ЭВМ.

Частотные методы, основанные на обратном преобразовании Фурье. Так как рассматриваемые в данном разделе линейные САУ заведомо устойчивы, т. е. все полюсы передаточной функции лежат слева от мнимой оси, то можно в преобразовании Лапласа считать σ₀ = 0 и перейти к преобразованию Фурье. Это позволяет произвести расчет переходного процесса при помощи аналитических или экспериментально найденных частотных характеристик, использованных нами ранее при изучении устойчивости САУ. Отсутствие необходимости решать характеристическое уравнение системы, а также хорошо разработанные способы расчета и возможность использования экспериментально найденных частотных характеристик делают эти методы весьма удобными.

Далее будет изложен один из таких методов.

1.12.3. Связь переходного процесса с вещественной частотной характеристикой системы.

Пусть исследуемая нами линейная САУ имеет частотную характеристику W(iω). Подадим на вход системы единичный импульс δ(t) и найдем весовую (импульсную) переходную функцию системы, использовав (П4.1.10):

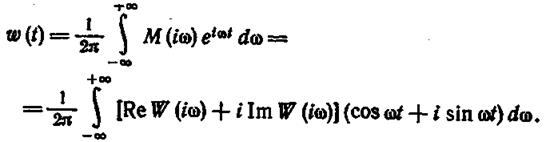       (1.12.10)

Здесь учтено, что δ(t)l1. Так как

где К(iω) и D(iω) – многочлены степени m и n (n > m) от iω, то

            (1.12.11)

(см. 1.12.10).

Так как

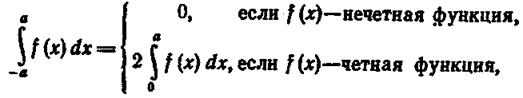
то, преобразуя интеграл, стоящий в правой части (1.12.10), получим

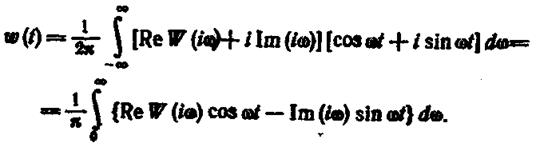         (1.12.12)

При отрицательных значениях времени оригинал тождественно равен нулю и, следовательно.

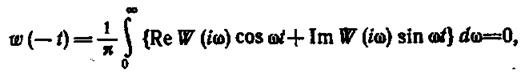                    (1.12.13)

откуда

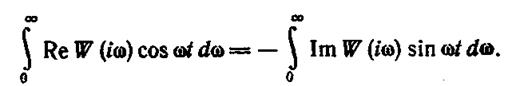            (1.12.14)

Таким образом, окончательно имеем

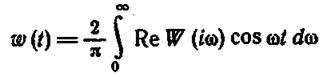                         (1.12.15)

или, что эквивалентно.

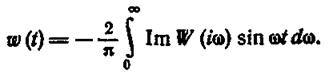                        (1.12.16)

Ранее нами была найдена связь между переходной функцией h(t) и весовой функцией w(t):

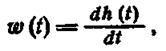                                          (1.12.17)

откуда, в соответствии с (1.12.15) находим