Качество систем автоматического управления, страница 3

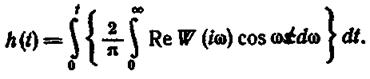
Меняя порядок интегрирования и учитывая, что

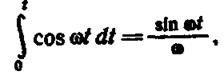
имеем

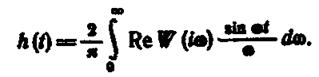                          (1.12.18)

Полученное нами уравнение (1.12.18) позволяет рассчитать переходный процесс системы по вещественной части комплексной частотной характеристики системы. На практике часто вещественная частотная характеристика задается таблицей или графиком, полученным из эксперимента. Но даже если для Re W(iω) имеется аналитическое выражение, то и тогда бывает, что непосредственное вычисление интеграла (1.12.18) затруднительно. Поэтому для этих целей обычно используют ЭВМ.

1.12.4. Интегральные оценки качества.

Прямые методы далеко не всегда приводят к успеху при исследовании показателей качества переходных процессов. Поэтому разработаны и широко применяются различные косвенные методы исследования качества процессов управления.

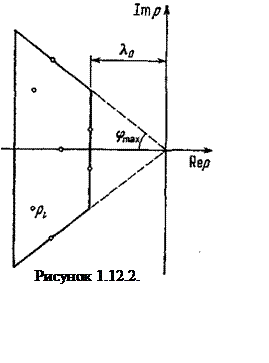
Например, если удается определить не сами корни, а только область расположения корней характеристического уравнения (рисунок 1.12.2.), то можно качественно оценить основные показатели переходного процесса. Так, величина λ₀ = |Re р_i|_min в какой-то степени будет характеризовать степень устойчивости САУ, а μ= |tgφ|_max - колебательность системы. Однако определение области на комплексной плоскости, заключающей все корни характеристического уравнения, оказывается также нелегкой задачей и имеет смысле для довольно узкого класса САУ. Поэтому, для того чтобы получить более или менее простыми средствами некое представление о каком-либо процессе управления в САУ, используют так называемые интегральные оценки качества.

Основная идея, заложенная в подобного рода оценках, состоит в том, чтобы охарактеризовать процесс управления одним числом, по величине которого было бы возможно сделать определенные выводы о протекании процесса в течение заданного интервала времени. В математике подобного вида оценки называются функционалами качества, и весьма часто они имеют вид

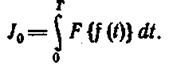                                         (1.12.19)

Как видно из (1.12.19), численное значение J₀ определяется видом функции F, временным ходом изучаемого процесса f(t) и интервалом времени протекания этого процесса (0,Т). Задачи оптимизации таких оценок решаются в общем случае вариационными методами. Здесь же рассмотрим наиболее простые интегральные оценки качества для исследования переходного процесса.

Пусть, как и ранее, исследуемые САУ описываются уравнением вида

                (1.12.20)

Будем считать, что x(t) = u(t), тогда, в силу определения h(t) имеем y(t) = h(t). Для удобства исследования качества переходного процесса произведем в (1.12.20) замену

т, е. выделим свободную составляющую переходного процесса - ее отклонение от установившейся величины h(∞). В этом случае неоднородное уравнение (1.12.20) превращается в однородное:

(1.12.21)

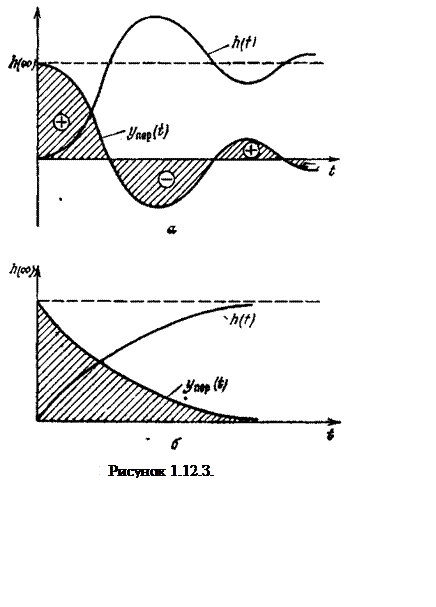
Рисунок 1.12.З. наглядно характеризует эту замену. Очевидно, что о качестве САУ можно судить как по h(t), так и по y_ПЕР(t). Обычно время окончания переходного процесса не может быть указано заранее. Поэтому в общем случае принимают Т=∞, что влечет за собой требование абсолютной интегрируемости F{y_ПЕР(t)}.

Линейной интегральной оценкой переходной составляющей называется определенный интеграл вида

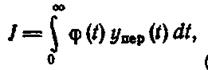(1.12.22)

где φ(t) - некая заранее известная функция времени, чаще всего равная l Если l = 0, то линейная интегральная оценка

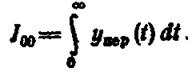(1.12.23)

представляет собой площадь, заключенную между кривой y_ПЕР(t) и осью времени t (заштрихована на рисунке 1.12.3.). Ёсли l ≠ 0

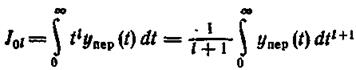                             (1.12.24)

- площадь между кривой y_ПЕР(t) и осью времени t, взятой в (l+1)-й степени. Оценка J₀₀ легко может быть вычислена. Из (1.12.21.) находим

                (1.12.25)