Понятие системы электропитания. Структура системы электропитания. Каналы электроснабжения, страница 2

Этим свойством обладают все реальные электрические цепи, поэтому они являются цепями с распределенными параметрами.

Так как в ряде технически важных задач не требуется знания электромагнитных процессов в каждой точке всей цепи и ее элементов, необходимо учесть только их интегральные свойства; такие цепи могут быть представлены в виде цепей с сосредоточенными параметрами, состоящих из сопротивлений, индуктивностей и емкостей. Например, катушка индуктивности может быть представлена в виде схемы с последовательным соединением сопротивления R, индуктивности L и с параллельно приключенной к ним емкостью C.

Электрическая сеть графически изображается в виде условной однолинейной схемы. На рисунке 2.2.1. показано графическое изображение ЛЭП, соединяющей источник питания (ИП), расположенный в пункте А, с ЭП, расположенным в пункте b. Места генерации и потребления энергии в сети изображаются кружком и стрелками. В месте генерации стрелка направляется к узлу, а в месте потребления – от узла. Возле стрелок указывается соответствующее значение полной мощности, которая для трехфазной сети в условиях симметрии и синусоидальности токов и напряжений является комплексной величиной.

Из электротехники известно, что произведение комплексов фазного напряжения U_Ф и тока I

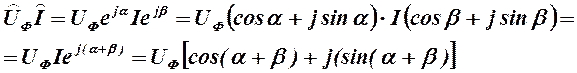   (2.2.1.)

не дает представления об активной и реактивной мощностях в отдельности, поскольку сумма углов α +β, входящая в выражение (2.2.1.), не равна углу сдвига фаз φ между векторами тока и напряжения, как это должно было бы быть для того, чтобы получить выражения активной мощности Р_Ф = U_Ф I cosφ и реактивной мощности Q_ф =U_ф I sinφ, где U_ф – модуль фазного напряжения; I – модуль тока. Для этого, очевидно, надо иметь α<0 или β<0, т.е. в основном выражении (2.2.1.) один из множителей должен быть сопряженной функцией (рисунок 2.2.2.).

Действительно, записав произведение прямого комплекса тока

                                (2.2.2.)

на сопряженный комплекс напряжения

                       (2.2.3.)

для индуктивной нагрузки при отставании вектора тока I от вектора напряжения U_Ф, т.е. когда α>β,получим

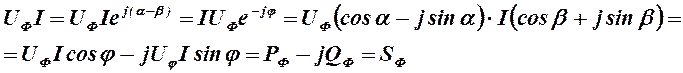                                                                                                             (2.2.4.)

Аналогично для емкостной нагрузки при опережении вектором тока I вектора напряжения U_Ф, т.е. когда β >α, будем иметь

            (2.2.5.)

Если же записать произведение прямого комплекса напряжения на сопряженный комплекс тока, то для индуктивной нагрузки

          (2.2.6.)

а для емкостной нагрузки

          (2.2.7.)

Таким образом, для обозначения полной мощности имеются два вида различных выражения, отличающиеся для одного и того же вида нагрузки только знаком реактивной мощности.

Для описания процессов в электрической сети переменного тока целесообразно использовать второе выражение полной мощности (2.2.3.), которое для трехфазного тока имеет вид

            (2.2.8.)

где S – мощность трех фаз; U – междуфазное (линейное) напряжение; I – ток в фазе.

Для энергетической характеристики работы электрической сети обычно достаточно знать значения активной (Р) и реактивной (Q) составляющих полной мощности (S), поскольку они определяются значениями нагрузки ЭП (у приемных концов сети), ИП (у передающих концов сети) и других элементов сети (ЛЭП, трансформаторов и т.д.).

Анализ энергетических процессов в цепи переменного тока показывает, что часть электроэнергии (активная составляющая) непосредственно преобразуется приемниками в другие виды энергии (тепловую, световую, механическую и т.п.) и теряется в элементах электрических сетей, выделяясь в виде тепла; другая же часть (реактивная составляющая), пропорциональная среднему за четверть периода значению энергии, расходуется на создание переменной составляющей электрического и магнитного полей индуктивностей, емкостей потребителей и элементов сети, частично теряясь в виде потоков рассеяния. За один период переменного тока реактивная энергия дважды отдается генератором в сеть и дважды возвращается обратно. Другими словами, реактивная мощность характеризует ту энергию, которой обмениваются генератор и приемник. Переменная составляющая электромагнитной энергии циркулирует между источником и потребителем в каждый полупериод, что необходимо для нормальной работы ЭП, работа которых основана на использовании электромагнитной энергии.