Другие предметы \ Испытания и контроль продукции

Прогнозирование надежности. Прогнозирование надежности с учетом предварительной информации, страница 6

4.  находятся частные потенциалы φg,I .

5.  частные потенциалы суммируются, и определяется знак полученного суммарного потенциала.

6.  по знаку суммарного потенциала выносится решение о том останется ли изделие надежным в течение определенного при обучении распознающей функции срока. Если окажется, что потенциал очень близок к точке перехода распознающей функции через 0, то весь процесс необходимо повторить, задав меньший интервал времени. Для этого собственно и необходимо обучение распознающей функции для различных интервалов времени. В конце процедуры выносят окончательное суждение о надежности изделия и указывают на какой интервал времени оно распространяется, т. е. в течение какого времени надежность контролируемого изделия будет иметь приемлемое значение.

ПЗ.6-7.4.5. Пример метода индивидуального прогнозирования качества изделия.

Определить распознающую функцию, если на обучение поставлено 10 приборов. В качестве контролируемых параметров выбраны: I, U2, U3. Параметр, определяющий работоспособность,– коэффициент усиления Ку. Признаком отказа является К<55. Измерение параметров производится в моменты времени t=0, а коэффициент усиления – через t = 1000 ч работы усилителя. Время прогнозирования, поэтому, равно 1000 ч.


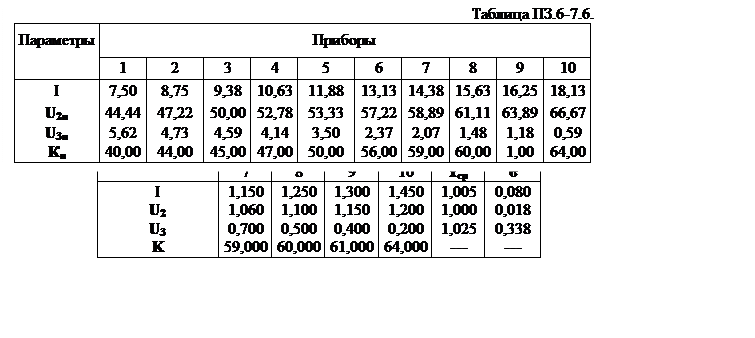На основании измерении контрольных параметров в процессе обучения составим таблицу по форме таблице ПЗ.6-7.5.

Произведем нормирование параметров по формуле хiн=хi/σ и заполним таблицу ПЗ.6-7.6.

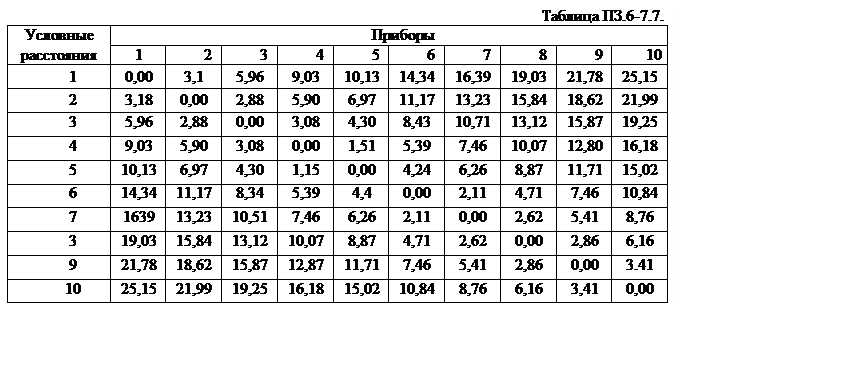
Вычислим коэффициенты связи — условные расстояния Rij — между значениями нормированных параметров по формуле

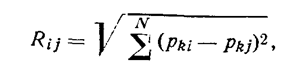
где i– номер основного прибора; j– номер прибора, связь с которым определяется: pki– k-й параметр i-го прибора; pkj– k-й параметр j-го прибора; N— число параметров.

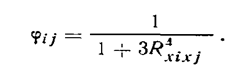
Подпись: Таблица ПЗ.6-7.7. Условные Приборы расстояния 1 2 3 4 5 6 7 8 9 10 1 0,00 3,1 5,96 9,03 10,13 14,34 16,39 19,03 21,78 25,15 2 3,18 0,00 2,88 5,90 6,97 11,17 13,23 15,84 18,62 21,99 3 5,96 2,88 0,00 3,08 4,30 8,43 10,71 13,12 15,87 19,25 4 9,03 5,90 3,08 0,00 1,51 5,39 7,46 10,07 12,80 16,18 5 10,13 6,97 4,30 1,15 0,00 4,24 6,26 8,87 11,71 15,02 6 14,34 11,17 8,34 5,39 4,4 0,00 2,11 4,71 7,46 10,84 7 1639 13,23 10,51 7,46 6,26 2,11 0,00 2,62 5,41 8,76 3 19,03 15,84 13,12 10,07 8,87 4,71 2,62 0,00 2,86 6,16 9 21,78 18,62 15,87 12,87 11,71 7,46 5,41 2,86 0,00 3.41 10 25,15 21,99 19,25 16,18 15,02 10,84 8,76 6,16 3,41 0,00

Значение Rij записываем в таблицу ПЗ.6-7.7. (R12=R21=3,18). В качестве распознающей функции принимаем

Формула получена экспериментальным путем. Частные значения распознающих функций, полученных на основании таблицы ПЗ.6-7.7., запишем в таблицу ПЗ.6-7.8.

Например, φ61=φ16= 1/(1+3*14,344=8*10-6.

Суммарное значение распознающей функции для каждого прибора определяется суммированием частных значений и записывается в таблицу ПЗ.6-7.8.

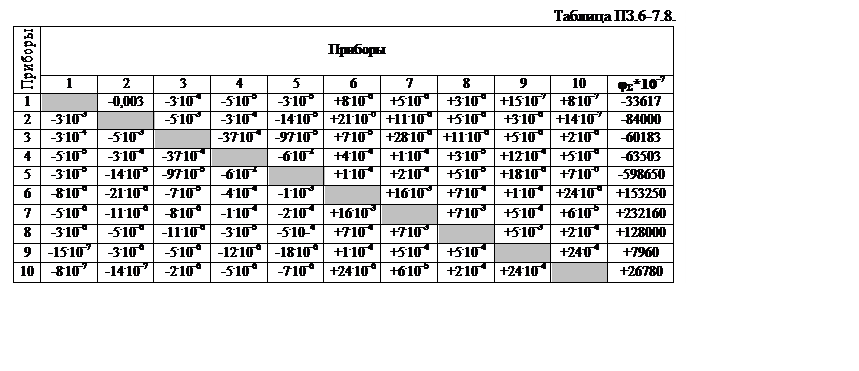Подпись: Таблица ПЗ.6-7.8. Приборы Приборы 1 2 3 4 5 6 7 8 9 10 φΣ*10-7 1 -0,003 -3.10-4 -5.10-5 -3.10-5 +8.10-6 +5.10-6 +3.10-6 +15.10-7 +8.10-7 -33617 2 -3.10-3 -5.10-3 -3.10-4 -14.10-5 +21.10-6 +11.10-6 +5.10-6 +3.10-6 +14.10-7 -84000 3 -3.10-4 -5.10-3 -37.10-4 -97.10-5 +7.10-5 +28.10-6 +11.10-6 +5.10-6 +2.10-6 -60183 4 -5.10-5 -3.10-4 -37.10-4 -6.10-2 +4.10-4 +1.10-4 +3.10-5 +12.10-4 +5.10-6 -63503 5 -3.10-5 -14.10-5 -97.10-5 -6.10-2 +1.10-4 +2.10-4 +5.10-5 +18.10-6 +7.10-6 -598650 6 -8.10-6 -21.10-6 -7.10-5 -4.10-4 -1.10-3 +16.10-3 +7.10-4 +1.10-4 +24.10-6 +153250 7 -5.10-6 -11.10-6 -8.10-6 -1.10-4 -2.10-4 +16.10-3 +7.10-3 +5.10-4 +6.10-5 +232160 8 -3.10-6 -5.10-6 -11.10-6 -3.10-5 -5.10-4 +7.10-4 +7.10-3 +5.10-3 +2.10-4 +128000 9 -15.10-7 -3.10-6 -5.10-6 -12.10-6 -18.10-6 +1.10-4 +5.10-4 +5.10-4 +24.0-4 +7960 10 -8.10-7 -14.10-7 -2.10-6 -5.10-6 -7.10-6 +24.10-6 +6.10-5 +2.10-4 +24.10-4 +26780

Например, φΣ1=-33617*10-7.

Таблица 1.7-8.15. - итоговая распознающая функция, позволяющая определить принадлежность испытуемого прибора либо к классу годных, либо к классу негодных по надежности: если φΣ меньше нуля, прибор не удовлетворяет требованиям.

Пример использования распознающей функции. Определить, к какому классу относится прибор, если его параметры I=0,8 A; U2=0,95 В; U3=l,5 В.

Ø Определим нормированные значения параметров исследуемого прибора: IН=10; U2Н= 52,78; U3Н,= 4,43.

Ø Найдем Ri,Н: R1,11=8,79; R2,11=5,71; R3,11=2,85; R4,11=0,22; R5,11=2,17; R6,11=5,81; R7,11=7,88; R8,11= 10,48; R9,11= 13,16; R10,11= 16,55.

Ø Определим наводимые потенциалы: φ1,11=– 6*10-5; φ2,11=–3*10-4; φ3,11=–5*10-3; φ4,11=-59*10-2;  φ5,11= –15*10-3; φ6,11 = +3*10–4; φ7,11= +9*10–6; φ8,11= +3*10–6; φ9,11= 1*10–5; φ10,11= 15*10-5.

Ø Суммарный потенциал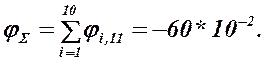

Так как суммарный потенциал имеет знак минус, то исследуемый прибор относится к классу В (см. рисунок ПЗ.6-7.2.), т. е. он не удовлетворяет требованиям надежности.

Индивидуальное прогнозирование не получило еще достаточно широкого применения в инженерной практике, но оно, несомненно, заслуживает внимания, так как такой контроль имеет чрезвычайно большое значение для изделий, входящих в состав систем. Он позволяет сделать вывод об индивидуальных свойствах исследуемого изделия. При удачно выбранной прогнозирующей функции и контролируемых параметрах можно контролировать индивидуальную надежность изделия и существенно сократить продолжительность контроля. Основная трудность этого контроля — в этапе обучения. Сокращение времени обучения может быть достигнуто использованием приемов сокращения объема и времени испытаний (аппроксимацией прогнозирующих параметров; использованием информации о надежности, полученной либо расчетно-аналитическим методом, либо методом моделирования).

Внедрение машинных методов для решения задач индивидуального прогнозирования - важная задача совершенствования контроля надежности в современной технике.

Скачать файл