Особенности имитации условий космического пространства при наземных испытаниях, страница 7

Уравнения (3.1.13.)…(3.1.19.) хорошо выполняются лишь при условии, что давление окружающей среды, по крайней мере, на порядок ниже равновесного давления пара (p_v<p_s) и что лишь пренебрежимо малое количество испаряющихся атомов или молекул возвращается к поверхности испарения. Если вакуум недостаточный (p_v ~ p_s), испарившиеся молекулы будут сталкиваться с молекулами остаточного газа и возвращаться к поверхности испарения. При этом фактическая скорость испарения будет ниже расчетной.

Аналогично введению понятия коэффициента “самозагрязнения” С_s может быть введен также коэффициент “загрязнения” С_c, учитывающий суммарное загрязнение исследуемой поверхности частицами, испаряющимися с нее при их повторном возвращении, а также “чужеродными” частицами со стенок и других элементов установки:

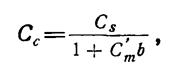                                       (3.1.20.)

где С^'_m — коэффициент откачки поверхностью объекта других газов.

Отсюда новая продолжительность формирования монослоя в условиях суммарного загрязнения исследуемой поверхности при условии:

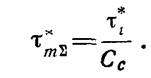                                            (3.1.21.)

Из рассмотрения уравнений (3.1.2), (3.1.3), (3.1.10), (3.1.20) следует, что коэффициенты, введенные в качестве критериев степени совершенства моделирования вакуумных условий космического пространства в лабораторных установках, взаимосвязаны.

Отметим, что если коэффициенты Z и Z₀ имеют скорее общее значение при оценке степени совершенства моделирования вакуумных космических условий и могут использоваться в расчетах при конструировании установок, то коэффициенты С_s, С_c, τ^*_m, τ^*_mΣ более применимы для расчетов при изучении поверхностных явлений, когда учет только коэффициентов Z недостаточен. Однако экспериментальные способы измерений указанных коэффициентов C_s, С_с, τ^*_m, τ^*_mΣ в настоящее время разработаны еще недостаточно хорошо.

3.1.4. Направленный характер действия давления в вакуумной камере испытательной установки.

Как уже говорилось, основным способом откачки при космическом моделировании является внутренняя откачка, осуществляемая насосами поверхностного действия. Поэтому, если в установках, использующих внешнюю откачку, вакуумные условия практически близки к изотропным, то в условиях внутренней откачки вакуумные условия отличаются существенной анизотропией. Распределение скоростей молекул остаточного газа, в этом случае, внутри установок уже не подчиняется закону Максвелла, а давление не является скалярной величиной. При этом в установках имеются неравновесные молекулярные потоки от исследуемого объекта к стенкам установки и от стенок установки по направлению к объекту в таких установках интенсивность потоков молекул от объекта к откачивающей стенке на несколько порядков выше, чем интенсивность потоков молекул, летящих в направлении объекта. Соответственно, давление на стенки может существенно превышать давление на испытуемый объект.

В общем случае давления на стенки и на объект не равны между собой и определяются следующим образом:

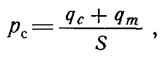                                          (3.1.22.)

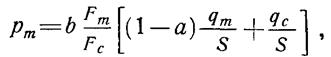                                  (3.1.23.)

где S- скорость откачки газа из установки; p_с – давление на стенку; p_m - давление на испытуемый объект; q_с – суммарная газовая нагрузка (натекание), создаваемая установкой; q_m - газоотделение объекта; F_m и F_с – площади поверхности объекта и внутренней стороны камеры соответственно; а - вероятность захвата молекулы стенкой; b - вероятность возврата молекулы, отраженной от стенки установки, на объект.

Из формулы (3.1.23.) следует, что только давление на стенки выражается обычной формулой типа 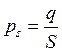. Если q_m >> q_c, то давление на объект будет равно

                                            (3.1.24.), где p_s – давление насыщенных паров материала поверхности объекта при температуре его поверхности T_s.

В случае газовой нагрузки в виде водяного пара вакуумный манометр, ориентированный на стенку, охлаждаемую жидким азотом, будет показывать давление на два порядка более низкое, чем манометр, ориентированный на объект испытаний.