Особенности имитации условий космического пространства при наземных испытаниях, страница 13

Тепловой поток q_T обусловленный молекулярной теплопроводностью, выражается различным образом в зависимости от соотношения между длиной свободного пробега молекул в рассматриваемом объеме газа и характерным размером этого объема. Для определения длины свободного пробега молекулы Λ можно воспользоваться уравнением Сюзерленда

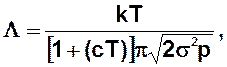           (3.1.32)

где k – (постоянная Больцмана); с – некоторая константа для газа; σ - диаметр молекулы; р – давление газа.

Тепловой поток за счет молекулярной теплопроводности, когда длина свободного пробега молекулы много меньше характерного размера системы Λ<< l (т. е. при сравнительно высоких давлениях), для системы двух параллельных плоскостей определяется выражением

                             (3.1.33)

а для соосных цилиндров

         (3.1.34)

где λ – коэффициент теплопроводности среды; ΔT - разность температур между пластинами или цилиндрами; l – расстояние между пластинами; d - диаметр внутреннего цилиндра; D – диаметр наружного цилиндра.

Величина q_T в формуле (3.1.33) отнесена к единице площади пластины, а в формуле (3.1.34) – к единице поверхности внутреннего цилиндра.

С уменьшением давления длина свободного пробега Λ резко возрастает и при давлениях порядка 10^-3…10^-4мм рт. ст. может достигать десятков сантиметров, что по порядку величины равно размерам системы. При Λ >> l

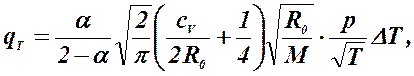                    (3.1.35)

где R₀ — универсальная газовая постоянная; М — молекулярная масса; α – коэффициент аккомодации, р – давление, .

Величина в (3.1.35) определена по формуле

                                             (3.1.36)

Формулу (3.1.35) можно представить в виде

                                               (3.1.37)

где 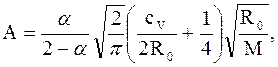 — константа, зависящая от типа газа и коэффициента аккомодации α и слабо зависящая от температуры. Значения константы А для некоторых газов можно найти в соответствующей литературе.

Использование формулы (3.1.35.) для цилиндрической системы возможно уже при давлении, обеспечивающем условие Λ ≥ l. Величина коэффициента аккомодации зависит от состояния поверхности и находится в пределах 0,1…0,9. Уравнение (3.1.35.) показывает, что в условиях, когда длина свободного пробега больше размеров системы, тепловой поток q_T пропорционален давлению газа р. Кроме того, тепловой поток пропорционален не градиенту температуры ΔT/ l, а просто разнице температур ΔT, т. е. характерный размер системы не влияет на величину теплового потока.

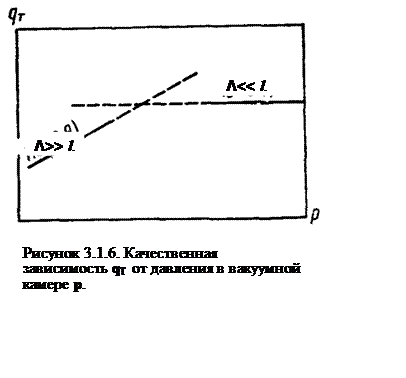Условно можно определить то давление р, при котором тепловые потоки по формулам (3.1.33) и (3.1.35.) равны друг другу (рисунок 3.1.6.). В действительности, тепловой поток в указанной точке будет меньше, поскольку в этой области совершается переход от режима сплошной среды (Λ << l) к разреженному газу (Λ >> l).

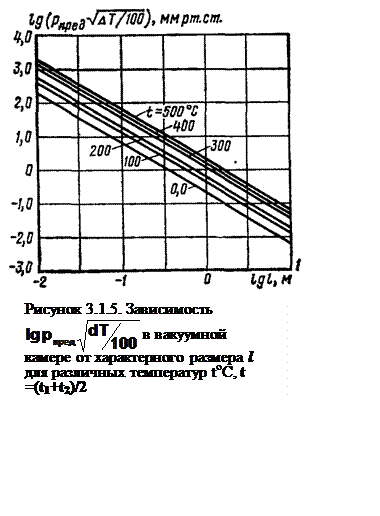
Из формул (3.1.33), (3.1.35.) и (3.1.32) следует, что при  отношение - зависит только от температуры, если считать, что газокинетический диаметр молекулы σ также зависит только от температуры.

В качестве примера в таблице 3.1.2. приведены данные расчета для ΔТ=700^оС и l=70 см в предположении, что коэффициент аккомодации α=1, а температура стенки камеры - Т_ω=300^оС. Для различных видов газа, в рассматриваемом примере, отношение Λ/l изменяется в пределах от 1,12 до 2,65.

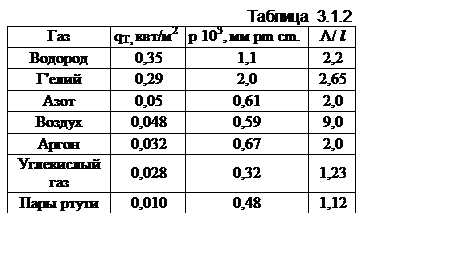Можно полагать, что реальные значения l будут отличаться от принятых в примере не более чем на порядок, а величина ΔT изменится не более чем в 2…3 раза. Тогда с учетом возможного перехода к формуле (3.1.34.) вместо формулы (3.1.33.) можно ожидать, что приведенные в таблице 3.1.2. значения р изменятся не более чем в 20…30 раз.

При испытаниях в вакуумной камере имеет значение не абсолютная величина теплового потока q , а его доля по отношению к лучистому тепловому потоку q_Л.

Рассмотрим величины лучистых потоков в исследуемой системе. Поток тепла, рассеиваемый поверхностью объекта при постоянной температуре и при условии диффузного излучения и отражения (т.е. при выполнении закона Ламберта), определяется формулой

                                    (3.1.38)