Особенности имитации условий космического пространства при наземных испытаниях, страница 5

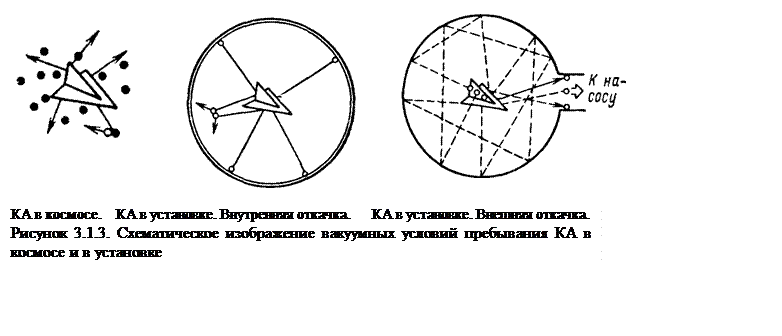
При полете КА в космическом пространстве лишь малая доля молекул, уходящих с него, будет возвращаться обратно (рисунок 3.1.3.) Это обстоятельство учитывается т. н. коэффициентом возврата. Коэффициент возврата Z₀ рассчитывается по отношению количества частиц, возвращающихся на КА в единицу времени к числу частиц, покидающих его поверхность. В космосе Z₀≠0 из-за взаимных столкновений сублимирующих с КА молекул образующих СВА. Этот коэффициент может быть оценен по уточненной формуле Боровика и Михайлова

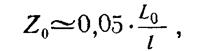                                   (3.1.1.)

где L₀ – характерный размер объекта; l – средняя длина свободного пробега молекул при давлении насыщенного пара вещества, испаряющегося или сублимирующего с поверхности КА.

Например, при давлении над поверхностью p_os≈10^-6 торр. для частиц с массой ~ 30 а. е. м. и L₀=1 м коэффициент возврата Z_o≈10^-8.

Обычно для космоса принимают Z₀≈10^-3…10^-4 .

3.1.3. Оценка неидентичности моделирования свойств космического пространства в лабораторных условиях.

В лабораторных условиях низкий коэффициент возврата можно получить в установке, имеющей стенки, подобные молекулярной ловушке. Если стенки установки не являются таковыми, то многие из молекул, покидающих исследуемый объект, будут отражаться от них и возвращаться на объект несколько раз до тех пор, пока не будут захвачены стенками (см. рисунок 3.1.3.).

Коэффициент возврата для этих условий определяется следующим образом:

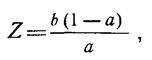                                            (3.1.2.)

где Z - коэффициент возврата, определяющий число столкновений молекулы с поверхностью объекта до ее откачки (Z>1) или вероятность попадания молекулы повторно на поверхность испарения (0<Z<1); b - вероятность возврата молекулы, отраженной от стенки установки, на объект; а - вероятность захвата молекулы стенкой.

Формула (3.1.2.) выведена в предположении, что коэффициент откачки (коэффициент захвата, коэффициент прилипания) поверхности объекта C_m равен нулю. В случае, когда C_m ≠ 0, коэффициент возврата –

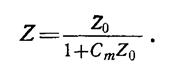                                       (3.1.3.)

Величина а определяется, как а = К*С_е, где К - доля откачивающей поверхности в общей площади внутренней поверхности камеры, а С_е - эффективный коэффициент откачки стенок установки.

Так как коэффициент С_е различен для различных газов, то и коэффициент Z будет неодинаков для различных газов. Поэтому обычно говорят о коэффициенте возврата по определенному газу (например, коэффициент возврата Z по азоту).

Ниже представлены формулы для расчета b – вероятности попадания на объект молекул, отраженных от поверхности установки.

Приведенные ниже формулы (3.1.4)…(3.1.9) выведены исходя из диффузного закона отражения молекул от стенок установки:

Случай 1. Испытательная камера и объект имеют сферическую форму (диаметры объекта и испытательной камеры соответственно - d_m и d_c):

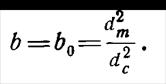                                          (3.1.4.)

Случай 2. Испытательная камера сферическая (диаметр d_c), объект цилиндрический (диаметр d_m, его длина L_m):

                                (3.1.5.)

Случай 3. Испытательная камера цилиндрическая (диаметр d_c, длина L_c), объект сферический (диаметр d_m)

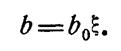                                                (3.1.6.)

Случай 4. Испытательная камера цилиндрическая (диаметр d_c, длина L_c), объект цилиндрический (диаметр d_m, длина L_m)

                                               (3.1.7)

Если внутренняя боковая поверхность испытательной камера представляет собой откачивающую поверхность (в случае применения т. н. «внутренней откачки»), то

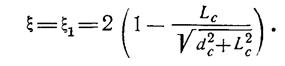                                         (3.1.8.)

Если торцы цилиндра представляют собой откачивающую поверхность, тогда

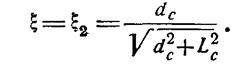                                       (3.1.9.)

Наименьший коэффициент возврата будет в том случае, когда отношение эффективной откачивающей поверхности ко всей поверхности близко к единице.

Произведем численную оценку коэффициентов возврата для случаев внешней и внутренней откачки. Для оценки принимаем коэффициент откачки объекта С_m = 0, так что Z = Z₀.