



Тема 2. Доходность финансовых операций. Реинвестирование.
Математическое и банковское дисконтирование.
Основные положения и формулы
1. Для сравнения доходности финансовых операций с различными сроками, ставками или условиями используют показатели, учитывающие временной период, в течение которого получен доход. Одним из показателей является эквивалентное значение годовой процентной ставки, доставляющей тот же доход, что и доход, получаемый в результате некоторой коммерческой сделки.

Так при выданном кредите под процентную ставку r доходность такой сделки для банка будет составлять:
· rдох = r, в случае, когда контракт не предусматривает дополнительных условий кредита;
· rдох > r, в случае наличия дополнительных условий контракта, например, комиссионных или внесение аванса по кредиту.
Доходность показывает среднегодовой рост капитала и учитывает все дополнительные условия финансового договора. Величина доходности не зависит от величины вложенного капитала (выданного кредита).
2. Капитализацией процентов называется процесс присоединения процентов к основному капиталу. Реинвестированием называется процесс начисления процентов на сумму, полученную в предыдущем периоде. Реинвестирование позволяет инвестору получить больший доход не только с величины начального капитала, но и с величины процентов, начисленных к концу предыдущего периода, так называемые "проценты на проценты".


3. Дисконтирование – это процесс определения любой, подлежащей к выплате в будущем суммы на более ранний момент времени в соответствии с некоторой ставкой. Говорят, что осуществляется приведение будущей суммы к настоящему моменту времени в соответствии с некоторой ставкой. В зависимости от вида используемой ставки (процентной или учетной) различают два вида дисконтирования: математическое (по процентной ставке) и банковское или коммерческое (по учетной ставке). В процессе дисконтирования искомую величину PV называют современной или приведенной стоимостью.
Математическое дисконтирование является процессом, обратным к наращению первоначального капитала по процентной ставке. Т.о. математическое дисконтирование есть процесс отыскания современной стоимости, зная будущую стоимость, срок и процентную ставку.
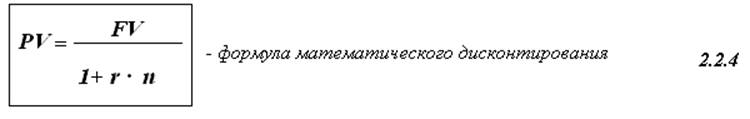


В краткосрочных операциях математического дисконтирования так же используют три схемы начисления процентов: английскую, французскую, немецкую.
4. Математическое дисконтирование можно осуществить для любого срока n.
5. Удобной и наглядной характеристикой процесса дисконтирования является коэффициент дисконтирования, показывающий, во сколько раз современная стоимость меньше будущей величины капитала.
 2.2.7
2.2.7
6.
Доход в операции дисконтирования часто называют дисконтом.
![]()
.
 2.2.8
2.2.8
7. Банковское (коммерческое) дисконтирование применяется в ситуациях:
· предварительного начисления процентов по кредиту и их одновременном удержании;
· учета ценной бумаги, например, векселя, заключающейся в покупке банком или другим финансовым учреждением векселя у владельца до наступления срока его погашения.
Банковское дисконтирование есть процесс определения суммы, подлежащей к выплате в будущем на более ранний момент времени в соответствии с учетной ставкой.
8. Вексель – ценная бумага, являющаяся письменным безусловным обязательством векселедателя выплатить в установленный срок определенную сумму держателю векселя.
Векселедатель – заемщик или должник, обязанный уплатить по векселю в указанный срок указанную в векселе сумму.
Векселедержатель – кредитор, имеющий право на получение денег по векселю.
Т.о. в векселе указана величина суммы и срок, по истечении которого эта сумма будет выплачена векселедержателю. Уплата денег по векселю называют его погашением.
Операция, заключающаяся в покупке банком или другим финансовым учреждением векселя у векселедержателя до наступления срока погашения по цене, меньшей той суммы, которая должна быть уплачена по векселю, называется его учетом. Сумма, которую получает векселедержатель при учете векселя - PV, называется дисконтированной величиной векселя. Проценты, удерживаемые банком в свою пользу, называют дисконтом. Будущую стоимость FV, указанную в векселе, называют его номиналом. Если специальным образом не оговорены условия, то вексель, как правило, учитывается по учетной ставке.
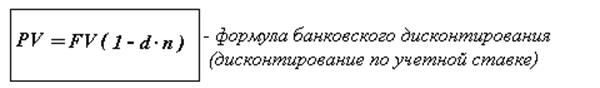 2.2.9
2.2.9
где n= nпогаш - nучета
nпогаш - срок погашения векселя
nучета – срок учета векселя в банке
Для срока, выраженного в месяцах и годовой учетной ставки, используют следующую формулу:
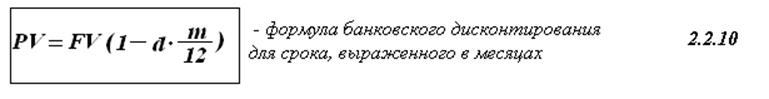
9. В краткосрочных операциях учета векселя, если это не оговорено в финансовом соглашении, как правило, начисляют обыкновенные проценты с точным числом дней.

10. Величина дохода банка (дисконта) при учете векселя составит:

11. Банковское
дисконтирование (в отличие от математического) возможно лишь для сроков 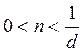
12. Математическое дисконтирование выгоднее для векселедержателя, банковское дисконтирование – для банка, т.к.
![]()
13. Удержание простых процентов в момент выдачи кредита тоже можно рассматривать как соглашение между кредитором и заемщиком о том, что наращение процентов будет осуществляться по простой учетной ставке. Тогда выданная на руки должнику сумма будет рассчитываться по формуле банковского дисконтирования 2.2.9, 2.2.10 или 2.2.11
14. Финансовый результат, полученный с помощью простой учетной ставки, можно получить и с помощью эквивалентной ей простой процентной ставки.


15. Финансовое соглашение может предусматривать не только фиксированную на весь срок учетную ставку, но и переменные учетные ставки, приуроченные к разным частям срока, а так же может быть установлена изменяющаяся во времени плавающая ставка.
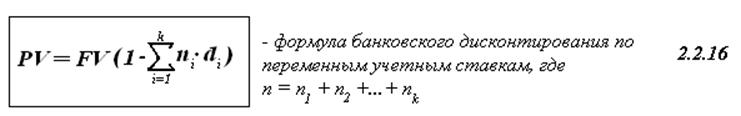

16. Можно рассчитать величину средней годовой учетной ставки простого процента, доставляющей при дисконтировании тот же доход, что и переменные учетные ставки.

17. Можно осуществлять наращение не только по процентной, но и по учетной ставке. Операцию учета векселя для банка можно считать операцией наращения за срок n = nпогаш - nучета. Таким образом, операция наращения простыми процентами по учетной ставке есть процесс обратный дисконтированию по учетной ставке.


Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.