Лекция 1
1.1. Определение. Разновидности матриц.
Матрицей размерности
mхn называется
прямоугольная таблица чисел, состоящая из m строк и n столбцов.
Матрицы обозначим заглавными буквами с «шапкой»: (![]() …):
…):
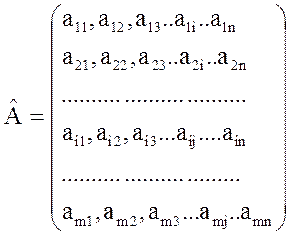
(матрицы
иногда указываются символом ![]() или
или ![]() )
)
Числа ![]() , из которых состоит матрица, называются матричными элементами матрицы, причем
первый индекс указывает номер строки, второй – номер столбца.
, из которых состоит матрица, называются матричными элементами матрицы, причем
первый индекс указывает номер строки, второй – номер столбца.
Иногда будем пользоваться обозначением:
![]()
Две матрицы
одинаковой размерности равны, если равны соответствующие матричные элементы: ![]()
Квадратной называется матрица, у которой m=n.
Матрица-столбец – это матрица размерностью mх1.
Удобно
обозначать матрицы-столбцы заглавными буквами ![]() …, с
перевернутой «шапкой» сверху:
…, с
перевернутой «шапкой» сверху:
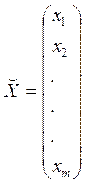
Матрица-строка - это матрица размерности 1хn.
Такие матрицы
удобно обозначать так: ![]() .
.
![]()
В дальнейшем матрицами-столбцами или матрицами-строками будем обозначать векторы (в конкретном базисе).
Пусть ![]() - квадратная матрица nxn.
Диагональными элементами называются элементы
- квадратная матрица nxn.
Диагональными элементами называются элементы ![]() . Они
образуют главную диагональ. Элементы
. Они
образуют главную диагональ. Элементы ![]() -
образуют побочную диагональ
-
образуют побочную диагональ
Диагональной называется матрица, у которой все недиагональные элементы равны нулю, и не все диагональные элементы равны нулю:
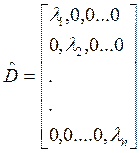
Единичной
называется диагональная матрица, у которой все диагональные элементы равны
единице. Единичную матрицу обычно обозначают буквами ![]() .
.
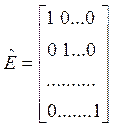
Введем понятие
символа Кронекера ![]() :
:
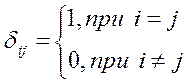 (1.1)
(1.1)
Тогда матричные элементы единичной матрицы можно представить в виде:
![]() (1.2)
(1.2)
а матричные элементы диагональной матрицы
![]() (1.3)
(1.3)
Очевидно, что:
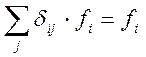
Нулевой
называется матрица ![]() , у которой все матричные
элементы равны нулю. (
, у которой все матричные
элементы равны нулю. (![]() )
)
Транспонированной
по отношению к ![]() называется матрица
называется матрица ![]() , элементы которой определяются следующим
образом:
, элементы которой определяются следующим
образом:
![]() (1.4)
(1.4)
Фактически ![]() получается из
получается из ![]() , если
все строки в
, если
все строки в ![]() заменим столбцами и наоборот. Наглядно,
транспонированная матрица получается из исходной, вращением на 180 градусов
вокруг главной диагонали, или путем «зеркального отображения» относительно
главной диагонали.
заменим столбцами и наоборот. Наглядно,
транспонированная матрица получается из исходной, вращением на 180 градусов
вокруг главной диагонали, или путем «зеркального отображения» относительно
главной диагонали.
Если ![]() =
=![]() , т.е.
, т.е. ![]() , то матрица называется симметричной.
, то матрица называется симметричной.
1.2. Действия над матрицами.
Выше мы рассмотрели разные таблицы чисел. По существу, эти таблицы становятся математическими объектами (матрицами), если определены следующие действия (композиции) над ними:
1.2. а) Сложение матриц
Пусть ![]() и
и ![]() -
матрицы одинаковой размерности mxn.
-
матрицы одинаковой размерности mxn.
Суммой ![]() +
+![]() матриц
матриц ![]() и
и ![]() называется
матрица
называется
матрица ![]() с матричными элементами
с матричными элементами
![]() (1.5)
(1.5)
В частности ![]() - переместительность,
- переместительность,
(![]() - сочетательность
- сочетательность
1.2. б) Умножение матрицы на число
Пусть ![]() - произвольная матрица mxn,
а
- произвольная матрица mxn,
а ![]() - произвольное вещественное число. тогда
- произвольное вещественное число. тогда ![]() . Новая матрица с матричными элементами
. Новая матрица с матричными элементами
![]() ,
(1.6)
,
(1.6)
т.е. при умножении матрицы на число все матричные элементы следует умножить на это число. Нетрудно убедиться, что
![]() ;
; ![]() ,
, ![]()
![]()
Очевидно, что ![]() ,
, ![]()
1.2. в) Произведение матриц
Пусть ![]() - матрица размерности mxk,
а
- матрица размерности mxk,
а ![]() - матрица размерности kxn.
Произведением
- матрица размерности kxn.
Произведением ![]() х
х![]() матриц
матриц ![]() и
и ![]() (в
указанном порядке) называется матрица
(в
указанном порядке) называется матрица ![]() с
матричными элементами:
с
матричными элементами:
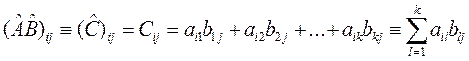 (1.7)
(1.7)
Как видно из
определения произведения матриц, при существовании ![]()
![]()
![]() , произведение
, произведение ![]()
![]() может не существовать.
Если
может не существовать.
Если ![]() и
и ![]() -
квадратные матрицы одинаковой размерности, то существуют произведения
-
квадратные матрицы одинаковой размерности, то существуют произведения ![]()
![]() и
и ![]()
![]() . Но в общем случае
. Но в общем случае
![]()
![]()
![]()
![]()
![]() .
.
Если ![]()
![]()
![]()
![]()
![]() , то матрицы
, то матрицы ![]() и
и ![]() называются коммутативными.
называются коммутативными.
Справедливы следующие утверждения для квадратных матриц:
![]() ,
,
![]() ,
(1.8)
,
(1.8)
![]() ,
,
Приведем доказательство последнего свойства. Имеем:
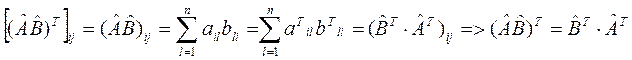
Пусть ![]() -
матрица размерности nxn,
-
матрица размерности nxn, ![]() - единичная матрица такой же
размерности. Нетрудно убедиться, что
- единичная матрица такой же
размерности. Нетрудно убедиться, что
![]() (1.9)
(1.9)
Действительно:
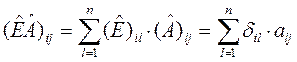
В последней сумме, согласно
определению ![]() (1.1), все слагаемые равны нулю, кроме
одного, когда
(1.1), все слагаемые равны нулю, кроме
одного, когда ![]() , т.е.
, т.е.
![]()
В частности ![]() .
.
Естественно,
можно определить степень матрицы ![]() , где
, где ![]() .
.
Например, ![]() ;
; ![]() .
.
1.2. г) Обратная матрица
Пусть ![]() - квадратная матрица nxn.
Обратной по отношению к
- квадратная матрица nxn.
Обратной по отношению к ![]() называется матрица
называется матрица ![]() , которая обладает следующими свойствами:
, которая обладает следующими свойствами:
![]()
![]() (1.10)
(1.10)
В дальнейшем
матричные элементы матрицы ![]() обозначим
обозначим ![]()
![]()
Следует запомнить, что 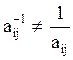 , т.е.
, т.е. ![]() не
обратное по отношению
не
обратное по отношению ![]() , это всего лишь обозначение
элементов матрицы
, это всего лишь обозначение
элементов матрицы ![]() .
.
Из определения (1.10) следует:
![]() .
.
С учетом (1.7) имеем:
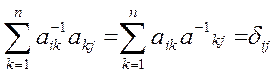
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.