К построению обратной матрицы мы вернемся позже. А сейчас убедимся в справедливости следующей формулы:
![]() (1.11)
(1.11)
Действительно, умножив (1.11)
слева на ![]() , получим
, получим
![]() <=>
<=>
![]() .
.
Получим тождество, следовательно, верно утверждение (1.11).
2. ОПРЕДЕЛИТЕЛИ
2.1. Определение
Из матричных элементов квадратной
матрицы ![]() размерности nxn
по определенному правилу образовывается число, которое называется определителем
(детерминантом) матрицы
размерности nxn
по определенному правилу образовывается число, которое называется определителем
(детерминантом) матрицы ![]() n-го
порядка и обозначается следующим образом:
n-го
порядка и обозначается следующим образом:
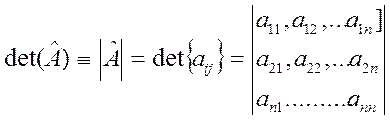
Прежде чем привести общее
определение определителя n-го порядка, рассмотрим некоторые
частные случаи. а) Определитель матрицы ![]() размерности 1х1.
размерности 1х1.
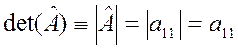 .
.
б) Определитель второго порядка
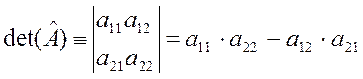 (2.1)
(2.1)
Чтобы привести определение определителя n-го порядка, нам понадобятся некоторые дополнительные понятия.
Рассмотрим совокупность первых n-натуральных чисел. Любую запись этих чисел в виде строки назовем перестановкой. Например, всевозможные перестановки из чисел 1, 2, 3:
(1,2,3); (2,1,3); (2,3,1); (3,2,1); (3,1,2); (1,3,2).
Обозначим через ![]() число всевозможных перестановок из n-чисел (элементов). Можно доказать, что
число всевозможных перестановок из n-чисел (элементов). Можно доказать, что
![]() (2.2)
(2.2)
Действительно,
при образовании всевозможных перестановок за первый элемент можно взять любое
из n-чисел (число вариантов – n).
При каждом конкретном выборе первого элемента, из остальных n-элементов
(чисел) можно образовать ![]()
![]() перестановок.
перестановок.
![]() ,
(2.3)
,
(2.3)
С очевидным условием
![]() (2.4)
(2.4)
Из рекуррентного соотношения (2.3) следует (с учетом (2.4)):
![]()
Пусть П – любая перестановка из n-чисел. Назовем инверсией любую пару чисел в перестановке, в которой большее число находится левее меньшего. В каждой перестановке имеется определенное число S (П) инверсий. Например, в перестановке (2, 4, 5, 1, 3) инверсии составляют пары: (2, 1); (4, 1); (5, 1); (4, 3); (5, 3).
Число инверсий S для данной перестановки равно 5. Условимся называть перестановку четной, если число инверсий – четное число, и нечетной – в противоположном случае.
Составим некое
произведение n-матричных элементов матрицы ![]() , взятых по одному (и только по одному) из
каждой строки и из каждого столбца. Напишем одно такое произведение:
, взятых по одному (и только по одному) из
каждой строки и из каждого столбца. Напишем одно такое произведение:
![]() (2.5)
(2.5)
Отметим, что
согласно правилу составления (2.5), как среди первых индексов ![]() , так и среди вторых -
, так и среди вторых - ![]() , не имеется совпадающих. Тогда в (2.3)
можно поменять местами множители так, чтобы первые индексы составляли порядок:
(1, 2, 3,…. n), т.е. представить (2.5) в виде
, не имеется совпадающих. Тогда в (2.3)
можно поменять местами множители так, чтобы первые индексы составляли порядок:
(1, 2, 3,…. n), т.е. представить (2.5) в виде
![]() (2.6)
(2.6)
Пусть число
инверсий в перестановке (![]() ) равно S (
) равно S (![]() ). Тогда число
). Тогда число
![]() (2.7)
(2.7)
называется членом определителя. Очевидно, что число таких членов n! (число всевозможных перестановок, образованных вторыми индексами).
Сумма n! членов вида (2.7) называется определителем матрицы ![]() :
:
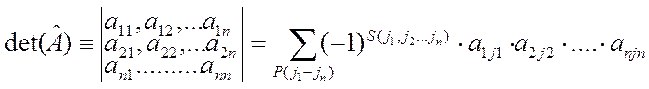 (2.8)
(2.8)
Здесь
суммирование проводится по всем возможным перестановкам между вторыми индексами
![]() .
.
Еще раз
подчеркнем, что каждое слагаемое типа (2.6) входит в сумму (2.8) со знаком (+),
если перестановка ![]() - четное (т.е. S – четное число), и со знаком (-), если перестановка
- четное (т.е. S – четное число), и со знаком (-), если перестановка ![]() - нечетное (т.е. S – нечетное число).
- нечетное (т.е. S – нечетное число).
2.2. Свойства определителей
Приведем некоторые очевидные утверждения:
а) ![]()
б) 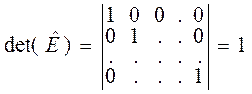 (2.9)
(2.9)
В случае а)
все члены типа (2.7) равны 0, т.к. все ![]() . Во
втором случае имеем лишь один, отличный от нуля член определителя:
. Во
втором случае имеем лишь один, отличный от нуля член определителя:
![]() , (т.к.
S=0).
, (т.к.
S=0).
Все свойства определителей, которые будут приведены ниже, вытекают из определения (2.8). Некоторые из этих свойств будут доказаны, некоторые будут приняты без доказательств.
Перечислим теперь важные свойства определителей.
1. Если все
элементы одной строки (столбца) матрицы равны 0, то определитель такой матрицы
равен 0. Действительно, в любом члене определителя (2.7) среди множителей ![]() один обязательно будет из «нулевой» строки
(столбца), т.е. один из множителей
один обязательно будет из «нулевой» строки
(столбца), т.е. один из множителей ![]() , следовательно, любой член
определителя равен 0.
, следовательно, любой член
определителя равен 0.
2. При транспонировании матрицы ее определитель не меняется, т.е.
![]() (2.10)
(2.10)
Это утверждение примем без доказательств.
3. Если поменять местами любые две строки (столбца), определитель поменяет знак. Для наглядности предположим, что местами меняются первые две строки:
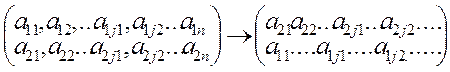
Следовательно,
значение нового определителя ![]() найдем, если в (2.8)
заменим
найдем, если в (2.8)
заменим ![]() , и
, и ![]() , т.е.
имеем
, т.е.
имеем
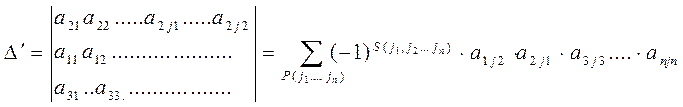 (2.11)
(2.11)
Член ![]() входит в (2.8) с множителем
входит в (2.8) с множителем ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.