График изменения вероятностей безотказной работы системы от времени работы (от наработки) Р=Р(t)

Задание

По структурной схеме надежности технической системы, минимальному значению вероятности безотказной работы системы γ и значениям интенсивности отказов λ_i необходимо:

1)  Построить график изменения вероятностей безотказной работы системы от времени работы (от наработки) Р=Р(t);

2)  Определить γ–процентный ресурс технической системы;

3)  Предложить способы увеличения γ-процентного ресурса не менее чем в 1,5 раза:

- повышением надежности элементов;

- структурным резервированием одного или нескольких элементов.

Все элементы системы работают в периоде нормальной эксплуатации. Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются «идеальными».

Решение

1.  В исходной схеме элементы 2, 3 образуют параллельное соединение. Заменяем их элементом А. Учитывая, что р₂ = р₃, получим:

р_А = 1 – q₂ · q₃ = 1 – q₂² = 1 – (1 – р₂)².                                             (1)

2.  Элементы 5, 6 также образуют параллельное соединение, заменив которое элементов В и учитывая, что р₅ = р₆ = р₂, получим:

р_В = 1 – q₅ · q₆ = 1 – q₂² = 1 – (1 – р₂)² = р_А.                                     (2)

3.  Элементы 8, 9 также образуют параллельное соединение, заменив которое элементов С и учитывая, что р₈ = р₉ = р₂, получим:

р_С = 1 – q₈ · q₉ = 1 – q₈² = 1 – (1 – р₈)² .                                   (3)

4.  Элементы 11, 12, 13, 14 образуют мажоритарное соединение «2 из 4», заменив которое элементом D. Так как р₁₁ = р₁₂ = р₁₃ = р₁₄, то для определения вероятности безотказной работы этого элемента можно воспользоваться комбинаторным методом:

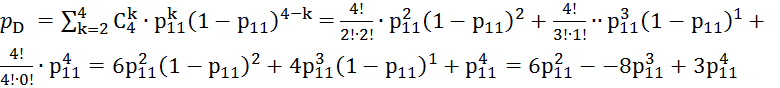                                                                                                (4)

5.  Преобразованная схема с элементами А, В, С и D представлена на рисунке 2:

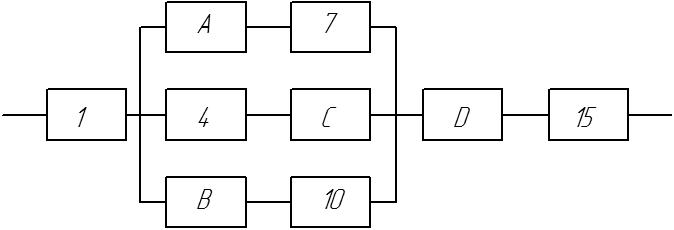
Рисунок 2 – Преобразованная схема

6.  В преобразованной схеме элементы A и 7, 4 и С, В и 10 создают последовательное соединение. Заменяем их элементами E, F и G, учитывая, что р₇ = р₁₀ = р₂, р_А = р_B. Соответственно, вероятность безотказной работы элементов E, F, G рассчитывается по формуле:

р_Е = р_А · р_{7 .}                                                                               р_F = р₄ · р_{C .}                                                                                         (5)

р_G = р_B · р_{10 .}

7.  Преобразованная схема с элементами E, F и G представлена на рисунке 3:

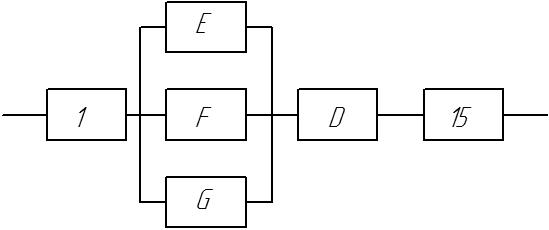
Рисунок 3 – Преобразованная схема

8.  В преобразованной схеме элементы E, F и G создают параллельное соединение. заменив которое элементом Н, получим:

Р_H = 1 – q_E · q_F · q_G .                                                                           (6)

9.  Преобразованная схема с элементом H представлена на рисунке 4:

Рисунок 4 – Преобразованная схема

10.  В преобразованной схеме все элементы создают последовательное соединение. Соответственно, вероятность безотказной работы системы рассчитывается по формуле:

Р = р₁ · р_Н · р_D· р₁₅.                                                                            (7)

11.  Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рисунок 1) подчиняется экспоненциальному закону:

р₁ = exp(–λ_i · t).                                                                                   (8)

12.  Результаты расчетов вероятностей безотказной работы элементов с 1 по 15 по формуле (8) для наработки до 2·10⁶ часов представлены в таблице 1.

13.  Результаты расчетов вероятностей безотказной работы квазиэлементов по формулам (1) – (4) также представлены в таблице 1.

14.  На рисунке 5 представлен график зависимости вероятности безотказной работы системы Р от времени наработки t.

15.  По графику (рисунок 5, кривая Р(t)) находим для γ = 70%               (γ–процентный ресурс системы) (Р_γ = 0,7), t_γ = 0,93·10⁶ ч.

16.  Проведенный проверочный расчет при t_γ = 0,93·10⁶ ч. показывает (таблица 1), что Р = 0,7006 ≈ 0,7.

17.  Рассчитываем повышенный в 1,5 раза γ–процентный ресурс системы: t_γ′ = 1,5 · 0,93·10⁶ = 1,395·10⁶ ч.

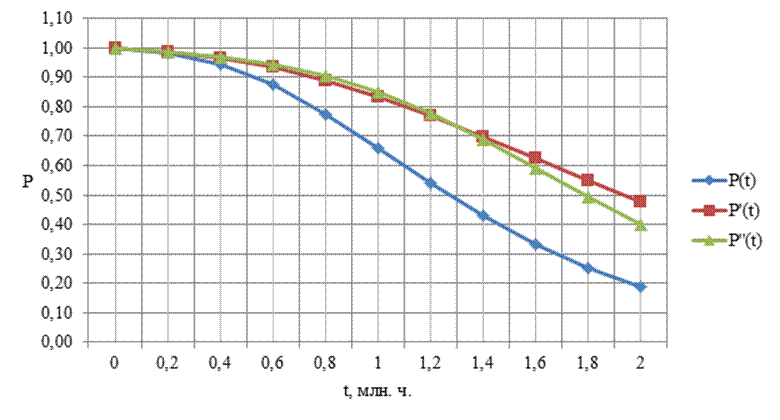
Рисунок 5 – Изменение вероятности безотказной работы системы

18.  Проведенный расчет показывает (таблица 1), при t = 1,395·10⁶ ч. для элементов преобразованной схемы (рисунок 4) р₁ = 0,9326, р_H = 0,4995,        р_D = 0,9528, р₁₅ = 0,9725. Следовательно, из четырех последовательно соединенных элементов минимальное значение вероятности имеет элемент Н, и увеличение его надежности даст максимальное увеличение надежности системы в целом.

19.  Для того, чтобы система при t_γ′ = 1,395·10⁶ ч. имела вероятность безотказной работы Р_γ = 0,7, необходимо, чтоб элемент Н имел вероятность безотказной работы (из формулы (7)):

                                                                                   (9)

.

Очевидно, что значение, полученное по формуле (9), является минимальным для выполнения условия увеличения ресурса не менее, чем в 1,5 раза, при более высоких значениях р_H увеличение надежности системы будет большим.

20.  Так как по условию все элементы системы работают в периоде нормальной эксплуатации и подчиняются экспоненциональному закону (8), то для элементов 2-6 при t = 1,395·10⁶ ч.:

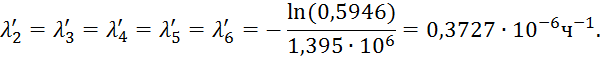
21.  Таким образом, для увеличения γ–процентного ресурса системы