Метод последовательного оценивания с использованием квадратичной аппроксимации (метод Пауэлла)
Метод основан на последовательном применении процедуры оценивания с использованием квадратичной аппроксимации.
Стратегия поиска
Задается начальная точка и с помощью пробного шага находятся три точки так, чтобы они были как можно ближе к искомой точке минимума. В полученных точках вычисляются значения функции. Затем строится интерполяционный полином второй степени, проходящий через имеющиеся три точки. В качестве приближения точки минимума берется точка минимума полинома. Процесс поиска заканчивается, когда полученная точка отличается от наилучшей из трех опорных точек не более, чем на заданную величину.
Алгоритм поисковой процедуры
Дано: х1, Dх, TOL1, TOL2
Шаг 1. Вычислить х2 = х1 + Dх.
Шаг 2. Вычислить f(х1) и f(х2).
Шаг 3. Если f(х1) > f(х2), положить х3 = х1 + 2Dх. Если f(х1) £ f(х2), положить х3 = х1 — Dх. Вычислить f(х3)
Шаг 4. Проиндексировать точки по порядку. Найти «наилучшую» точку
![]() ,
,
Xmin = точка хi, которая соответствует Fmin.
Шаг 5. По трем точкам х1, х2, х3 построить аппроксимирующий полином (найти коэффициенты а0, а1, а2).
Шаг 6. Вычислить
![]() , используя формулу для оценивания с
помощью квадратичной аппроксимации.
, используя формулу для оценивания с
помощью квадратичной аппроксимации.
Шаг 7. Проверка на окончание поиска.
(а)
Если [Fmin– f(![]() )] / f(
)] / f(![]() )≤TOL1,
)≤TOL1,
(б)
и если [Хmin — ![]() ]/
]/ ![]() ≤TOL2 ®end: x*=
≤TOL2 ®end: x*=![]()
Иначе ® Шаг 8.
Шаг 8. Выбрать
“наилучшую” точку (Хmin или ![]() ) и две точки по обе стороны от нее.
Обозначить (проиндексировать) эти точки в естественном порядке и перейти к шагу
5.
) и две точки по обе стороны от нее.
Обозначить (проиндексировать) эти точки в естественном порядке и перейти к шагу
5.
Заметим, что при первой реализации шага
5 границы интервала, содержащего точку минимума, не обязательно оказываются
установленными. При этом полученная точка ![]() может
находиться за точкой х3. Для того чтобы исключить возможность
слишком большого экстраполяционного перемещения, следует провести после шага 5
дополнительную проверку и в случае, когда точка
может
находиться за точкой х3. Для того чтобы исключить возможность
слишком большого экстраполяционного перемещения, следует провести после шага 5
дополнительную проверку и в случае, когда точка ![]() находится
слишком далеко от х3, заменить
находится
слишком далеко от х3, заменить ![]() точкой,
координата которой вычисляется с учетом заранее установленной длины шага.
точкой,
координата которой вычисляется с учетом заранее установленной длины шага.
Задание: f(x) = (100-x)2; x1 = 92; Dх = 7, TOL1 = TOL2 = 0,01.
Практическая работа 7
Методы с использованием производных
Требования к функции: унимодальность, непрерывность, дифференцируемость
Врамках схемы Ньютона – Рафсона предполагается, что функция f дважды дифференцируема. Работа алгоритма начинается в точке х1, которая представляет начальное приближение (или начальную оценку) координаты стационарной точки, или корня уравнения f‘(х) = 0. Затем строится линейная аппроксимация функции f‘(х) в точке х1,и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения.

Алгоритм
Дано: f(x); x0, TOL
Шаг 1: f’(x); f”(x)
Шаг 2: ![]()
Шаг 3: f’(xk+1); f”(xk+1)
Шаг 4: Если |f’(xk+1) | ≤ TOL ® end: x*≈xk+1
Иначе ® Шаг 2.
Задание:
f(x) - своя; x0 = а, TOL=0,01
7.2. Метод средней точки (Больцано)
Определим две точки L и R таким образом, что f‘(L) < 0 и f’(R) > 0. Стационарная точка расположена между L и R. Вычислим значение производной функции в средней точке рассматриваемого интервала z = (L+R)/2. Если f’(z) > 0, то интервал (z, R) можно исключить из интервала поиска. С другой стороны, если f‘(z) < 0, то можно исключить интервал (L, z). Ниже дается формализованное описание шагов алгоритма.
Алгоритм
Дано: f(x); (a;b), TOL
Шаг 1. f’(x)
Шаг 2.R = b, L = a; при этом f‘(а) < 0 и f’(b) > 0.
Шаг 3.z = (R + L)/2 и f’(z).
Шаг 4. Если |f’(z)’| £TOL® end: x*≈ z.
Иначе ® Шаг 5.
Шаг 5. Если f’(z) < 0 ®L = z ® шаг 3
Если f’(z) > 0® R=z ® шаг 3.
Задание:
f(x) - своя; (a; b), TOL=5
Метод секущих,являющийся комбинацией метода Ньютона и общей схемы исключения интервалов, ориентирован на нахождение корня уравнения f’(х) = 0 в интервале (а, b), если, разумеется, такой корень существует.

Предположим, что в процессе поиска стационарной точки функции f(х) в интервале (а, b) обнаружены две точки L и R, в которых знаки производной различны. В этом случае алгоритм метода секущих позволяет аппроксимировать функцию f‘(х) “секущей прямой” (прямой линией, соединяющей две точки) и найти точку, в которой секущая графика f‘(х) пересекает ось абсцисс (рис. 2.16). Таким образом, следующее приближение к стационарной очке х*определяется по формуле
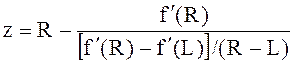 .
.
Если |f’(z)| £e,поиск следует закончить. В противном случае необходимо выбрать одну из точек Lили R таким образом, чтобы знаки производной в этой точке и точке z были различны, а затем повторить основной шаг алгоритма.
Алгоритм
Дано: f(x); x0, TOL
Шаг 1: L:=a; R:=b
Шаг 2: f’(L); f’(R)
Шаг 3: 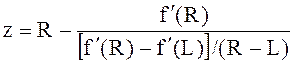
Шаг 4: Если |f’(xk+1) | ≤ TOL ® end: x*≈xk+1
Иначе ® оставляем z в качестве одной из границ, а второй границей
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.