






5. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Задача 39.
Дано высказывание ![]() : "Если будет хорошая
погода и Алексей встретится с Настей, то они пойдут в парк". Требуется:
: "Если будет хорошая
погода и Алексей встретится с Настей, то они пойдут в парк". Требуется:
1)
Выделить в высказывании ![]() атомарные
высказывания,
атомарные
высказывания,
2)
Представить ![]() в виде формулы логики высказываний с
использованием импликации,
в виде формулы логики высказываний с
использованием импликации,
3)
Составить таблицу истинности высказывания ![]() ,
,
4)
Представить ![]() в виде формулы логики высказываний
без импликации.
в виде формулы логики высказываний
без импликации.
Решение.
1. Атомарные высказывания;
![]() :"будет
хорошая погода",
:"будет
хорошая погода",
![]() :"Алексей
встретится с Настей",
:"Алексей
встретится с Настей",
![]() :"Алексей
пойдет в парк",
:"Алексей
пойдет в парк",
![]() :"Настя
пойдет в парк".
:"Настя
пойдет в парк".
2. ![]()
![]() - представление высказывания
- представление высказывания ![]() в виде формулы логики высказываний.
в виде формулы логики высказываний.
3. Таблица истинности высказывания ![]() :
:
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
4. Имея таблицу высказывания ![]() ,
можно составить СДНФ(
,
можно составить СДНФ(![]() ) и СКНФ(
) и СКНФ(![]() ).СДНФ составляют на единичном
наборе, а СКНФ – на нулевом наборе булевой функции.
).СДНФ составляют на единичном
наборе, а СКНФ – на нулевом наборе булевой функции.
Поскольку нулевой набор высказывания ![]() значительно короче, чем единичный
набор (3 нуля и 13 единиц) составим СКНФ формулы
значительно короче, чем единичный
набор (3 нуля и 13 единиц) составим СКНФ формулы ![]() :
:
![]()
![]() .
.
Задача 40. Дана формула алгебры высказываний
![]()
![]() , где атомарные высказывания
, где атомарные высказывания ![]() ,
, ![]() ,
, ![]() и
и ![]() определены
в задаче 39.
определены
в задаче 39.
Требуется:
1) Упростить формулу.
2) Составить отрицание высказывания ![]() ,
,
3) Записать отрицание высказывания ![]() в виде формулы, содержащей импликацию
и перевести ее в текст.
в виде формулы, содержащей импликацию
и перевести ее в текст.
Решение.
1. Пользуясь свойствами булевых операций, получим цепочку преобразований:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. Составим отрицание высказывания ![]()
![]() :
:
![]()
![]() .
.
3. Пользуясь равенством ![]() ,
запишем высказывание
,
запишем высказывание ![]() , используя импликацию:
, используя импликацию:
![]()
![]()
![]()
![]() .
.
Переведем высказывание ![]()
![]() в текст:
в текст:
"Если будет плохая погода, или Алексей не встретит Настю, или он пойдет в парк, то при том, что погода станет хорошей, а Алексей и Настя встретятся, Настя в парк не пойдет".
Задача 41. Даны
формулы алгебры высказываний: ![]() ,
, ![]() ,
, ![]() .
.
Найти среди них тавтологии и тождественно ложные формулы.
Решение.
Составим таблицы истинности указанных в условии высказываний:
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
Ответ: ![]() –
тавтология,
–
тавтология, ![]() – тождественно ложная формула,
– тождественно ложная формула, ![]() – выполнимая формула.
– выполнимая формула.
Задача 42. Записать
формулы ![]() ,
, ![]() ,
,
![]() в алгебре
в алгебре ![]() и
упростить их.
и
упростить их.
Решение.
Пользуясь формулами перехода от импликации и
эквиваленции ![]() ,
, ![]() к
операциям конъюнкции, дизъюнкции и отрицания, представим формулы в алгебре
к
операциям конъюнкции, дизъюнкции и отрицания, представим формулы в алгебре ![]() и упростим их.
и упростим их.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
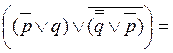
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Задача 43. Задан
одноместный предикат ![]()
![]() тогда
и только тогда, когда
тогда
и только тогда, когда ![]() ",
", ![]() . Покажите на числовой оси множество
истинности предиката.
. Покажите на числовой оси множество
истинности предиката.
Решение.
Запишем ![]() в виде
предикатной формулы.
в виде
предикатной формулы.
![]() , где
, где ![]()
![]() ",
",
![]() "
"![]() ".
".
Запишем предикатную формулу в алгебре ![]() :
:
![]()
![]()
![]() .
.
Пусть ![]() и
и ![]() множества истинности предикатов
множества истинности предикатов ![]() и
и ![]() соответственно.
Множество истинности предиката
соответственно.
Множество истинности предиката ![]()
![]() есть множество
есть множество ![]() , предиката
, предиката ![]()
![]() -
- ![]() .
Множеством истинности предиката
.
Множеством истинности предиката ![]()
![]() является пересечение множеств
является пересечение множеств ![]() и
и ![]() .
.
Следовательно, множеством истинности предиката ![]() является множество
является множество ![]()
![]() .
.
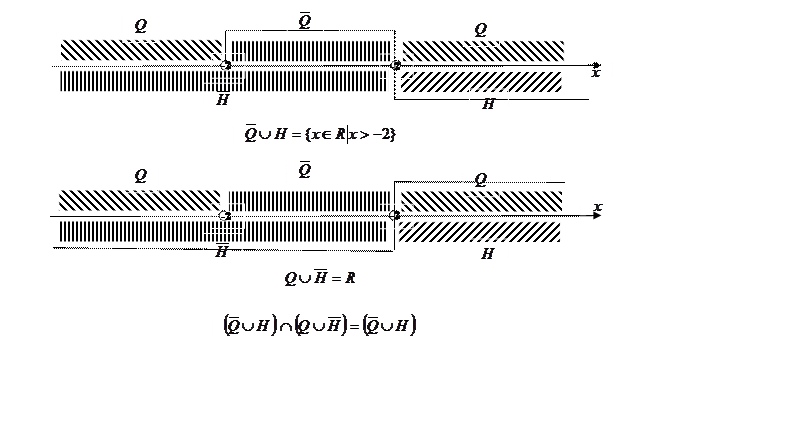
Отметим на числовой оси множества ![]() ,
, ![]() ,
, ![]() и
и ![]() .
Как видно из рисунка
.
Как видно из рисунка ![]()
![]()
![]() .
.
Задача 44. Задан
трехместный предикат ![]() "если число
"если число ![]() делится на число
делится на число ![]() , то их сумма меньше
, то их сумма меньше ![]() ", где
", где ![]() .
Требуется:
.
Требуется:
1.Выделить атомарные предикаты и запишите ![]() предикатной формулой.
предикатной формулой.
2. Найти множество истинности каждого атомарного
предиката и всего предиката ![]() .
.
3. Проиллюстрировать найденные множества диаграммами Эйлера-Венна.
Решение.
1. Атомарные предикаты:
![]() "число
"число ![]() делится на число
делится на число ![]() ",
",
![]() .
.
![]()
![]()
![]() .
.
2. ![]()
![]()
![]()
![]() .
.
Множество истинности предиката ![]() есть
множество
есть
множество ![]() , где
, где ![]() и
и
![]() - множества истинности предикатов
- множества истинности предикатов ![]() и
и ![]() соответственно.
соответственно.
Выбрав из множества ![]() тройки
элементов, в которых первый элемент не делится на второй, получим множество
тройки
элементов, в которых первый элемент не делится на второй, получим множество ![]() .
.
![]()
![]()
![]() .
.
Выбрав из множества ![]() тройки
элементов, в которых сумма первых двух элементов меньше третьего, получим
множество
тройки
элементов, в которых сумма первых двух элементов меньше третьего, получим
множество ![]() .
.
![]() .
.
Объединив множества ![]() и
и
![]() , получим множество истинности
предиката
, получим множество истинности
предиката ![]()
![]()
![]() :
:
![]()
![]()
![]()
![]()
![]() .
.
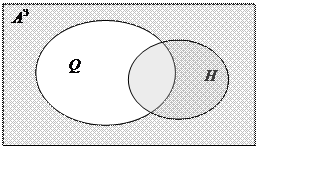
3. Диаграмма Эйлера-Венна представлена на рисунке. Множество A3 является универсальным множеством в данной задаче.
Множества Q и H
пересекаются. Во множество ![]() истинности
предиката
истинности
предиката ![]() попадают все элементы множества H и все элементы, не входящие в множество Q.
Множество
попадают все элементы множества H и все элементы, не входящие в множество Q.
Множество ![]() на диаграмме – область, отмеченная
цветом.
на диаграмме – область, отмеченная
цветом.
Задача 45. Задан
двуместный предикат ![]() :
: ![]() ,
где
,
где ![]() ,
, ![]() .
Представьте множества истинности и множества ложности предикатов
.
Представьте множества истинности и множества ложности предикатов ![]() ,
, 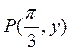 ,
,
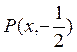 в системе координат на плоскости.
Запишите два истинных и два ложных высказывания, получаемые из предиката
в системе координат на плоскости.
Запишите два истинных и два ложных высказывания, получаемые из предиката ![]() подстановкой значений переменных.
подстановкой значений переменных.
Решение.
 Множеством истинности предиката
Множеством истинности предиката ![]() является волна синусоиды на отрезке
является волна синусоиды на отрезке ![]() (см. рис.). Все точки прямоугольника
(см. рис.). Все точки прямоугольника
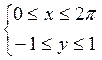 , за исключением множества точек
синусоиды, являются множеством ложности этого предиката.
, за исключением множества точек
синусоиды, являются множеством ложности этого предиката.
Одноместный предикат
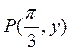 :
: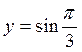 определен на множестве
определен на множестве ![]() , его множество истинности –
, его множество истинности – 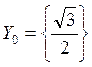 , множество ложности
, множество ложности
– 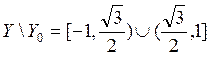 .
.
Одноместный предикат 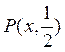 :
: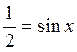 определен на множестве
определен на множестве ![]() , его множество истинности –
, его множество истинности – 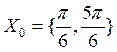 , множество ложности –
, множество ложности – 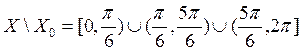 .
.
Задача 46.
Задан двуместный предикат ![]() :
: ![]() .
.
Требуется:
1) найти множество истинности и множество ложности ![]() ,
,
2) составить и записать словами всевозможные предикаты и высказывания применяя кванторные операции. Для каждого предиката найти множество истинности и множество ложности, а для каждого высказывания – его значение истинности.
Решение.
1) Областью определения предиката ![]() является множество
является множество ![]() . Чтобы найти множества истинности и
ложности предиката
. Чтобы найти множества истинности и
ложности предиката ![]() составим таблицу.
составим таблицу.
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
Множество истинности предиката ![]() :
:
![]() , множество ложности предиката
, множество ложности предиката ![]() :
: ![]() .
.
2) Составим одноместные предикаты и высказывания,
связывая переменные предиката ![]() кванторами
существования и всеобщности. Каждый полученный предикат или высказывание будем
переводить в текстовую форму и оценивать истинность или ложность.
кванторами
существования и всеобщности. Каждый полученный предикат или высказывание будем
переводить в текстовую форму и оценивать истинность или ложность.
1. ![]()
![]() – одноместный предикат.
– одноместный предикат.
![]() : "при любом
значении
: "при любом
значении ![]() ,
, ![]() ".
Свободная переменная –
".
Свободная переменная – ![]() ; множество истинности -
; множество истинности - ![]() , множество ложности -
, множество ложности - ![]() .
.
2. ![]()
![]() – одноместный предикат.
– одноместный предикат.
![]() : "существуют
такие значения
: "существуют
такие значения ![]() , при которых
, при которых ![]() ". Свободная переменная –
". Свободная переменная – ![]() ; множество истинности -
; множество истинности - ![]() , множество ложности -
, множество ложности - ![]() .
.
3. ![]()
![]() – одноместный предикат.
– одноместный предикат.
![]() : "каким бы
ни было значение
: "каким бы
ни было значение ![]() ,
, ![]() ".
Свободная переменная –
".
Свободная переменная – ![]() ; множество истинности -
; множество истинности - ![]() , множество ложности -
, множество ложности - ![]() .
.
4. ![]()
![]() – одноместный предикат.
– одноместный предикат.
![]() : "найдутся
такие значения
: "найдутся
такие значения ![]() , при которых
, при которых ![]() ". Свободная переменная –
". Свободная переменная – ![]() ; множество истинности -
; множество истинности - ![]() , множество ложности -
, множество ложности - ![]() .
.
5. ![]()
![]()
![]() –
ложное высказывание.
–
ложное высказывание.
![]() : "при любых
значениях переменных
: "при любых
значениях переменных ![]() и
и ![]() верно,
что
верно,
что ![]() ".
".
6. ![]()
![]()
![]() –
истинное высказывание.
–
истинное высказывание.
![]() : "существуют
такие значения
: "существуют
такие значения ![]() , что при любых значениях
, что при любых значениях ![]() истинно неравенство
истинно неравенство ![]() ".
".
7. ![]()
![]()
![]() –
истинное высказывание.
–
истинное высказывание.
![]() : "при любом
значении
: "при любом
значении ![]() найдется такое значение
найдется такое значение ![]() , что окажется истинным неравенство
, что окажется истинным неравенство ![]() ".
". ![]() .
.
8. ![]()
![]()
![]() –
истинное высказывание.
–
истинное высказывание.
![]() : "найдутся
такие значения переменных
: "найдутся
такие значения переменных ![]() и
и ![]() , что неравенство
, что неравенство ![]() окажется истинным".
окажется истинным".
Задача 47. Составить
и записать словами отрицание ![]() высказывания
высказывания ![]() :
: ![]() ,
если
,
если ![]() "если
"если ![]() и
и
![]() делится на
делится на ![]() ,
то
,
то ![]() делится на
делится на ![]() "
(
"
(![]() ). Определить значение истинности
). Определить значение истинности ![]() и
и ![]() .
.
Решение.
Составим отрицание высказывания ![]() :
: ![]()
![]() .
.
Предикат ![]() является
импликацией
является
импликацией ![]() ,
,
где
![]() "
"![]() ",
",
![]() "
"![]() делится
на
делится
на ![]() ",
", ![]() "
"![]() делится на
делится на ![]() ".
".
Представим ![]() в виде дизъюнкции:
в виде дизъюнкции:
![]()
![]()
![]() .
Тогда высказывание
.
Тогда высказывание ![]() можно прочесть следующим
образом:
можно прочесть следующим
образом:
"Каково бы ни было число ![]() ,
найдутся такие числа
,
найдутся такие числа ![]() и
и ![]() ,
что хотя бы одно из следующих утверждений будет истинным
,
что хотя бы одно из следующих утверждений будет истинным ![]() ,
или
,
или ![]() не
делится на
не
делится на ![]() или
или ![]() является
делителем
является
делителем ![]() ".
".
Такое высказывание истинно. В самом деле, выбрав ![]() , легко видеть, что по крайне мере
утверждение "1 является делителем
, легко видеть, что по крайне мере
утверждение "1 является делителем ![]() "
оказывается истинным для любого натурального числа
"
оказывается истинным для любого натурального числа ![]() .
.
Составим отрицание предиката ![]() :
:
![]()
![]() .
.
Высказывание ![]()
![]() можно прочесть следующим образом:
можно прочесть следующим образом:
"Найдется такое число ![]() ,
что каковы бы ни были числа
,
что каковы бы ни были числа ![]() и
и ![]() , будет справедливо утверждение
, будет справедливо утверждение ![]() и
и ![]() делится
на
делится
на ![]() , но
, но ![]() на
на
![]() не делится".
не делится".
Поскольку высказывание ![]() является
истинным, его отрицание
является
истинным, его отрицание ![]() ложно.
ложно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.