Экономика и менеджмент \ Надежность систем управления

Выполнить расчет надежности системы управления

Страницы работы

18 страниц (Word-файл)

Скачать файл

Содержание работы

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

Санкт-Петербургский государственный технологический университет растительных полимеров

Отчет по лабораторным работам

по дисциплине

"Надежность систем управления"

Выполнил:

Крупенькин Е.В. гр.531

Проверил:

доц. Хмельницкий А. К.

Санкт-Петербург

2011 г.

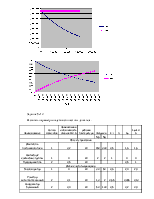
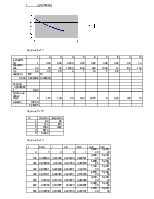
Задание № 1

N0=	100
dt	0-100	100-200	200-300	300-400	400-500	500-600	600-700	700-800
	3	5	3	6	5	4	2	1

dt	Q(dt)	P(dt)
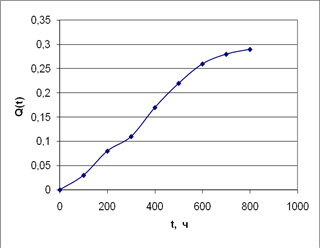
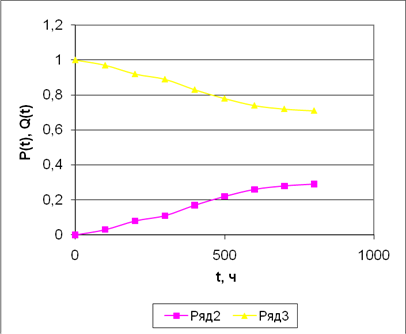
0	0	1
100	0,03	0,97
200	0,08	0,92
300	0,11	0,89
400	0,17	0,83
500	0,22	0,78
600	0,26	0,74
700	0,28	0,72
800	0,29	0,71

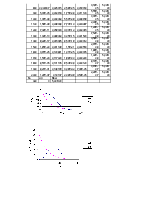
Задание № 2

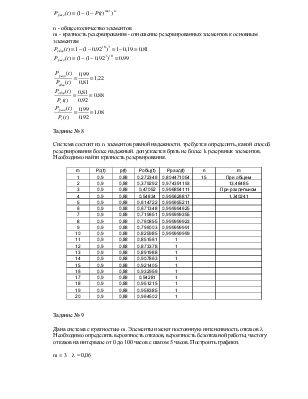
P(50) = 0,9 P(150) = 0,47

Найти P(50, 150), Q(50, 150)

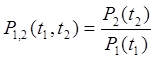
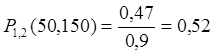
Задание № 3

Р1(50) = 0,93

Р2(50) = 0,91

Р3(50) = 0,95

Р4(50) = 0,78

Р5(50) = 0,85

Р6(50) = 0,75

Р7(50) = 0,69

Р8(50) = 0,74

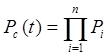
Р_с(50) = 0,2

Задание № 4

р₈(100) = 0,93

Р_с(t) = р(t)ⁿ

P_c(100) = 0,93⁸ = 0,56

Задание № 5

p_i(100) = 0,98 N = 24

P_c(t) = 0,98²⁴ = 0,62

При увеличении на 0,005

P_c(t) = 0,985²⁴ = 0,696

Надежность увеличилась на 12,3%

Задание № 6

Нерезервированная система состоит из 8 элементов. необходимо определить показатели надежности системы λ_с(t) - ?, T_ср(t) - ?

λ₁ = 0,0005

λ₂ = 0,00004

λ₃ = 0,00008

λ₄ = 0,00009

λ₅ = 0,00005

λ₆ = 0,0002

λ₇ = 0,00009

λ₈ = 0,0005

λ_с(t) = Σλ_i

λ_c(t) = 0,00155

T_cp(t) = 1/ λ_c(t)

T_cp(t) = 645,1613

Задание № 7

Система состоит из n элементов равной надежности. требуется определить, какой способ резервирования более надежный. допускается брать не более k резервных элементов.

P(t) = 0,92

n = 10

k = 20

n - общее количество элементов

m - кратность резервирования - отношение резервированных элементов к основным элементам

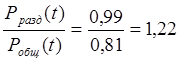
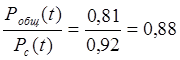
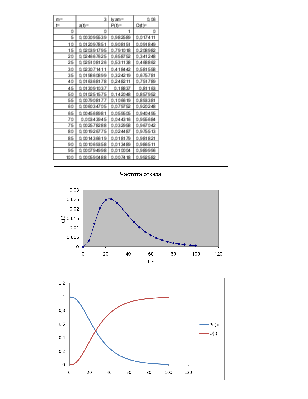
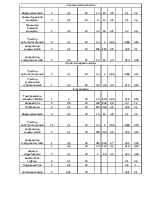
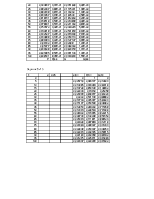
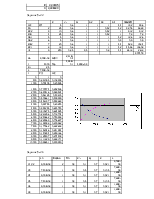
Задание № 8

Необходимо найти кратность резервирования.

m	Pc(t)	p(t)	Pобщ(t)	Pразд(t)	n	m
1	0,9	0,88	0,272346	0,804471054	15	При общем
2	0,9	0,88	0,379292	0,974391193		13,48485
3	0,9	0,88	0,47052	0,996894111		При раздельном
4	0,9	0,88	0,54834	0,999626817		1,340241
5	0,9	0,88	0,614722	0,999955211
6	0,9	0,88	0,671348	0,999994625
7	0,9	0,88	0,719651	0,999999355
8	0,9	0,88	0,760855	0,999999923
9	0,9	0,88	0,796003	0,999999991
10	0,9	0,88	0,825985	0,999999999
11	0,9	0,88	0,851561	1
12	0,9	0,88	0,873378	1
13	0,9	0,88	0,891988	1
14	0,9	0,88	0,907863	1
15	0,9	0,88	0,921405	1
16	0,9	0,88	0,932956	1
17	0,9	0,88	0,94281	1
18	0,9	0,88	0,951215	1
19	0,9	0,88	0,958385	1
20	0,9	0,88	0,964502	1

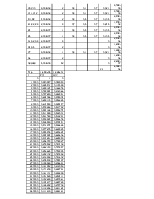
Задание № 9

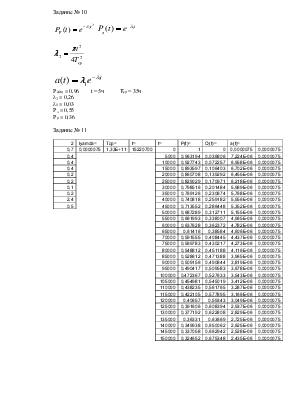
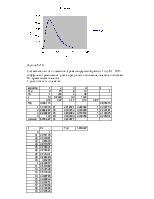
Дана система с кратностью m. Элементы имеют постоянную интенсивность отказов λ. Необходимо определить вероятность отказов, вероятность безотказной работы, частоту отказов на интервале от 0 до 100 часов с шагом 5 часов. Построить графики.