


Тест по курсу
"Дискретная математика"
Вариант 7
1. На диаграмме Эйлера-Венна изображены множества ![]() ,
, ![]() и
и
![]() .
.
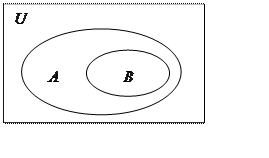
Какое из включений верно: а) ![]() , б)
, б) ![]() ,
в)
,
в)![]() , г)
, г)![]() ?
?
2. Даны множества ![]() ,
,
![]() ,
, ![]() .
Характеристическая функция множества
.
Характеристическая функция множества ![]() может
быть представлена вектором:
может
быть представлена вектором:
а)
![]() , б)
, б) ![]() ,
в)
,
в)![]() , г)
, г) ![]() .
.
3. Прямые ![]() заданы
уравнениями:
заданы
уравнениями:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Матрицей
бинарного отношения ![]() перпендикулярна
перпендикулярна ![]() , (
, (![]() )
является матрица:
)
является матрица:
а) б) в) г)
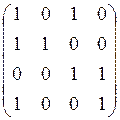
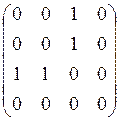
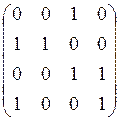
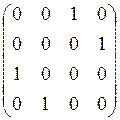 .
.
4. Бинарное отношение ![]() ,
задано матрицей
,
задано матрицей 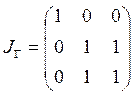 ,
, ![]() ,
,
![]() . Транзитивным замыканием отношения
. Транзитивным замыканием отношения ![]() является множество:
является множество:
а)
![]() ,
,
б)
![]() ,
,
в)
![]() ,
,
г)
![]() .
.
5. Взаимно однозначное соответствие ![]() , где
, где ![]() ,
задано двустрочной матрицей:
,
задано двустрочной матрицей:
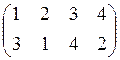 . Двустрочной матрицей обратного
соответствия является матрица:
. Двустрочной матрицей обратного
соответствия является матрица:
а) б) в) г)
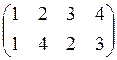 ,
, 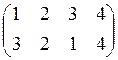 ,
, 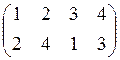 ,
,
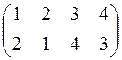 .
.
6. Множества ![]() ,
, ![]() и
и ![]() содержат
пять, три и четыре элемента соответственно. Число способов, которыми можно
составить тройку элементов из каждого множества равно
содержат
пять, три и четыре элемента соответственно. Число способов, которыми можно
составить тройку элементов из каждого множества равно
а) 60, б) 30, в) 12, г) 120.
7. В группе 15 девушек и 10 юношей. Число способов, которыми можно составить танцевальную пару из юноши и девушки равно
а) 25, б) 1015, в) 1510, г) 150.
8. СДНФ эквиваленции ![]() булевых
переменных
булевых
переменных ![]() и
и ![]() является
формула
является
формула
а) ![]() , б)
, б) ![]() ,
в)
,
в) ![]() , г)
, г) ![]() .
.
9. Булева функция от трех переменных задана единичным набором: (0, 2,3,4,5). Карта Карно для этой функции имеет вид:
|
а) |
б) |
в) |
г) |
|||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||
10. Составное высказывание ![]() "Если
число153 делится на 3 и на 5, то оно делится на 15" может быть записано
формулой:
"Если
число153 делится на 3 и на 5, то оно делится на 15" может быть записано
формулой:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() ,
г)
,
г) ![]() .
.
11. Формулу логики высказываний ![]() можно записать в виде следующей ДНФ:
можно записать в виде следующей ДНФ:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() ,
г)
,
г) ![]() .
.
12. Отрицание высказывания ![]() можно
прочесть так:
можно
прочесть так:
а) "Найдется такой ![]() ,
что для любых
,
что для любых ![]() и
и ![]() ложно
хотя бы одно из утверждений
ложно
хотя бы одно из утверждений ![]() , или
, или ![]() , или
, или ![]() ",
",
б) "Для любого ![]() найдутся
такие
найдутся
такие ![]() и
и ![]() ,
что утверждения
,
что утверждения ![]() ,
, ![]() и
и
![]() – ложны",
– ложны",
в) "Для любого ![]() найдутся
найдутся
![]() и
и ![]() ,
при которых ложно хотя бы одно из утверждений
,
при которых ложно хотя бы одно из утверждений ![]() ,
или
,
или ![]() , или
, или ![]() ",
",
г) "Существуют такие ![]() ,
, ![]() и
и ![]() ,
для которых утверждения
,
для которых утверждения ![]() ,
, ![]() и
и ![]() –
ложны".
–
ложны".
13. Орграф ![]() задан списком
ребер
задан списком
ребер 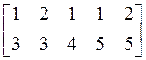 . Его матрицей инциденций является
матрица:
. Его матрицей инциденций является
матрица:
а) б) в) г)
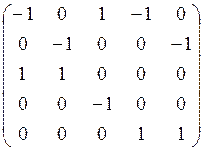 ,
, 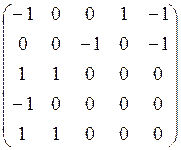 ,
,
 ,
,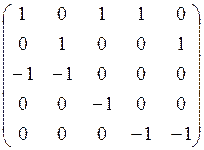 .
.
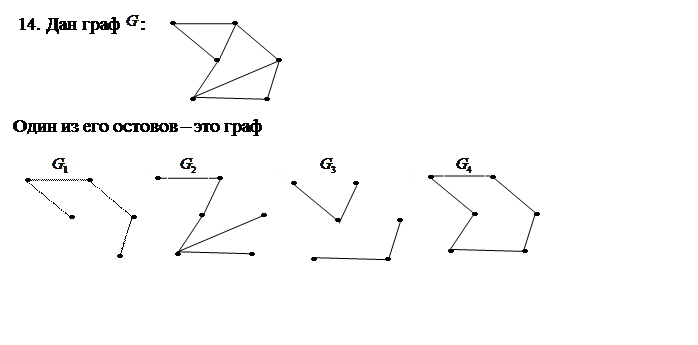 |
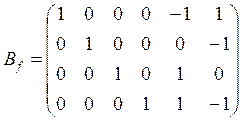 .
.
Матрицей базисных разрезов этого графа является матрица:
а) 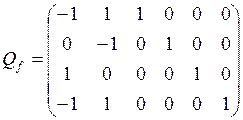 ,
б)
,
б) 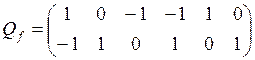 ,
,
в) 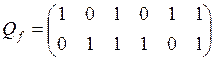 ,
г)
,
г) 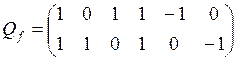 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.