зрения, использование логики в качестве подходящей ступени на этом длинном пути является естественным и плодотворным. Поскольку именно логика сопровождает процесс мышления человека с момента зарождения интеллекта.
Конечно, логика давно используется и при проектировании компьютеров, и при анализе компьютерных программ. Однако непосредственное использование логики в качестве языка программирования, называемого логическим программированием, возникло сравнительно недавно.
Логическое программирование, так же, как и родственное ему направление – функциональное программирование, радикально отклоняется от основного пути развития языков программирования. Логическое программирование строится не с помощью некоторой последовательности абстракций и преобразований, отталкивающейся от машинной архитектуры фон Неймана и присущего ей набора операций, а на основе абстрактной модели, которая никак не связана с каким-либо типом машинной модели. Логическое программирование базируется на убеждении, что не человека следует обучать мышлению в терминах операций компьютера, а компьютер должен выполнять инструкции, свойственные человеку.
Язык Пролог прошел длинный путь развития (почти 40 лет). Он продолжает весьма быстро распространяться.
Целью настоящего курса является изучение и практическое освоение средств логического программирования для решения научных и прикладных задач. Основными задачами преподавания данной дисциплины является обучение студентов теоретическим основам логического программирования, технологии программирования на языке Prolog в среде Visual Prolog v 4.x и выше, освоение студентами основ теории экспертных систем и теории графов, привития навыков отладки и тестирования программ с использованием средств Visual Prolog. Обучение практическому программированию осуществляется на основе языка логического программирования Prolog в среде Visual Prolog v 4.0 с учетом знаний и умений, полученных при изучении курса в течение семестра.
В рамках дисциплины
выполняется: студентами, обучающимися 5 лет по специальности 220400 – три расчетно-графических задания, студентами,
обучающимися 3,5 года, – два
расчетно-графических задания (номера 2 и 3). Студентами, обучающимися 5
лет по специальности 351400 – два расчетно-графических задания (номера 2
и 3), студентами, обучающимися 3,5 года, –
одно расчетно-графическое задание (номер 3).
Номер варианта определяется последней цифрой номера зачетной книжки следующим образом: к последней цифре зачетной книжки прибавляется 1, например, если последний номер 1, то ему соответствует вариант 2, если последняя цифра – 9, то слушатель выполняет вариант номер 10.
Отчет по каждому расчетно-графическому заданию сдается в письменном виде. Пример выполнения и оформления расчетно-графического задания приводится на лазерном диске, с электронным обучающим курсом.
После изучения курса сдается письменный экзамен. Экзаменационный билет составляется из экзаменационных вопросов и задач, приведенных в пособии.
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АВТОМАТИЧЕСКОГО
ДОКАЗАТЕЛЬСТВА ТЕОРЕМ
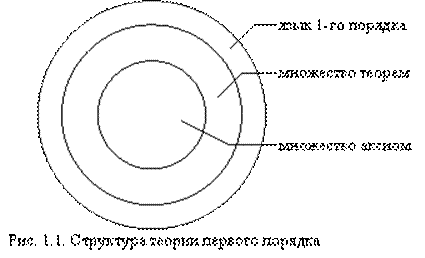
1.1. Теории первого порядка
Любая теория первого порядка состоит из следующих объектов: языка первого порядка, представляющего множество правильно построенных выражений (утверждений); конечного множества утверждений, называемых аксиомами; конечного множества правил вывода вида x1, x2,…,xn ® y1, y2,…,ym, означающих, что если все утверждения x1,…,xn являются аксиомами или теоремами, то утверждения y1,…,ym - теоремы. Аксиомы и правила вывода выделяют во множестве правильно построенных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.