Решить задачу коммивояжера методом перебора с возвратом. Цены билетов заданы с помощью симметричной n´n матрицы.

Министерство образования  и науки Российской федерации

Комсомольский-на-Амуре государственный технический университет

Факультет компьютерных технологий

Кафедра МОП ЭВМ

Лабораторная работа №2

по дисциплине: САОД (Часть 2)

                Студент  группы 3ВТ-1                                          Юрченко А.С.

                Вариант                                                                   4         

                Преподаватель                                                        Изабеков З.А.

Комсомольск-на-Амуре     

 2006 г.

Задание:

Решить задачу коммивояжера методом перебора с возвратом. Цены билетов заданы с помощью симметричной  n´n  матрицы.

Ход работы:

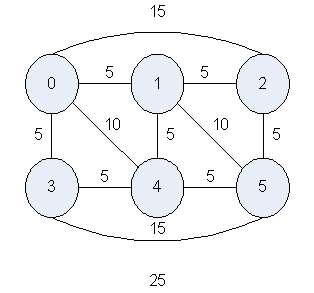Задан граф (рисунок 1) представляющий схему пути перемещения. Для решения задачи коммивояжера необходимо обойти все города и вернутся в исходный за минимальную цену, т.е. эта задача сводится к поиску гамильтоново цикла в графе, с минимальными значениями путей между узлами.

В этой задаче надо перебрать все гамильтоновы циклы и найти среди них наименьший.

Задача перебора гамильтоновых циклов. Путь будем представлять в виде последовательности вершин (x₁,x₂,…,x_k). Такой путь будет простым если и только если x_i = x_j для всех i¹j, i,jÎ{1,2,…,k}.

Определим предикаты.

P_k(x₁,x₂,…x_k)=1 Û x_i¹x_j, при 1 £ i < j £ k, и {x_i,x_i+1} – ребра при 1 £ i < k;

Q(x₁,x₂,…x_k)=1 Û k=n и {x_n,x₁} – ребро.

Для того, чтобы последовательности вершин (x₁,x₂,…x_k) удовлетворяли условию x_i¹x_j, будем раскрашивать вершины этих последовательностей и учитывать раскраску при выборе очередей вершины. Гамильтонов цикл, с началом x₁=n₀, представим как последовательность (x₁,x₂,…,x_n,x_n+1), где x_n+1=x₁=n₀.

Пусть A_k – множество вершин, смежных с x_k, c_n - раскраска вершины n_.  Согласно общей схеме имеем следующий приближенный текст для перебора гамильтоновых циклов;

Листинг программы:

#include <iostream.h>         //библиотека ввода-вывода

#include <conio.h>            //консольный ввод-вывод

void gamilton(int);           //подпрограмма гамильтонова цикла

void print();                 //подпрограмма подсчёта суммы

int graph[6][6] =       //граф

{

{ 0,  5, 15,  5, 10, 25},

{ 5,  0,  5,  0,  5, 10},

{15,  5,  0,  0,  0,  5},

{ 5,  0,  0,  0,  5, 15},

{10,  5,  0,  5,  0,  5},

{25, 10,  5, 15,  5,  0}

};

int u, v, u0, v0;       //начальные и текущии координаты перебора графа

int sum, minsum = 32000;      //текущая и мин. сумма

int minput[6];                //мин. путь

int put[6];             //текущий путь

int main()              //главная подпрограмма

{

u0 = v0 = 0;               //устанавливаем координаты в начало

u = u0;             

v = v0;             

graph[v0][u0] = 1;        

gamilton(0);               //запускаем перебор графа

print();

cout << "Min put: " << endl;    //вывод "Min put: "

for (int i = 0; i < 6; i++)

cout << " " << minput[i] << " ";//вывод мин. пути

cout << endl << "cost: " << minsum << endl;//вывод суммы

getch();             //задержка экрана

}

void gamilton(int hod)        //подпрограмма гамильтонова цикла

{

int i;

for (i = 0; i <= 5; i++)

{

if (i != v && graph[i][v])

{

if (i == v0 && hod == 5)

{

print();

}

if (!(graph[i][i]))

{

v = i;

put[hod] = i;     //текший город записываем в путь

graph[i][i] = 1;

gamilton(hod + 1);  //рекурсивный вызов

graph[i][i] = 0;

v = i;

}

}

}

}

void print()            //подпрограмма подсчёта суммы

{

sum = 0;       //текущая сумма =0

int i;

for (i = 0; i < 5; i++)

{

sum += graph[put[i]][put[i + 1]]; //сумируем цену пути

}

sum += graph[put[i]][put[0]];

if (sum < minsum)    //если тек. сумма < минимальной:

{

minsum = sum;

for (int i = 0; i < 6; i++)

minput[i] = put[i];

}

}

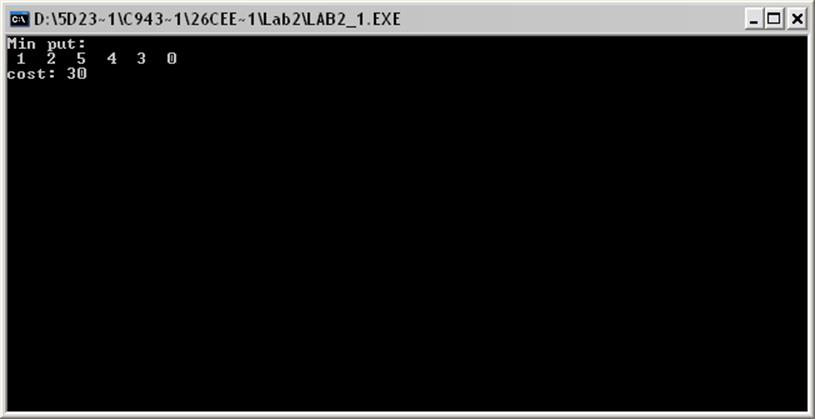
Результат выполнения программы: