










Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Комсомольский-на-Амуре государственный
технический университет»
Факультет компьютерных технологий
Кафедра «МОП ЭВМ»
ЛАБОРАТОРНАЯ РАБОТА №2
по курсу «Метрология, стандартизация и сертификация»
Студент группы 4ВС-1 Лоушкин А.В.
Преподаватель: Муратова Т.А.
Комсомольск-на-Амуре
2006
Тема: «Оптимизация программного кода с использованием TURBO PROFILER»
Цель работы: Научиться оптимизировать программу, используя статистические данные
Задание: Оптимизировать с помощью системы Turbo Profiler программный модуль, написанный на языке СИ.
Выполнение: В качестве оптимизируемой программы выбран пример, реализующий метод интерполяции с равномерным шагом для нахождения узлов интерполяции. При сборе статистических данных в Turbo Profiler число запусков программы равнялось десяти.
Исходный текст программы(5(1).срр)
#include <stdio.h>
#include <conio.h>
#include <math.h>
float A,B;
float Xi[27],Yi[27];
float Ai[27],Bi[27],Ci[27],Di[27];
float Alpha[27],Betta[27];
float h;
int n;
float fn (float x)
{
return (1/(1+24*x*x));
}
float fsh (float x)
{
return (-(48*x)/pow(1+24*x*x,2));
}
float Sx (float x)
{
int i=int((x-A)/h);
return Ai[i]+Bi[i]*(x-Xi[i])+Ci[i]*(x-Xi[i])*(x-Xi[i])+Di[i]*(x-Xi[i])*(x-Xi[i])*(x-Xi[i]);
}
float Sshx (float x)
{
int i=int((x-A)/h);
return Bi[i]+2*Ci[i]*(x-Xi[i])+3*Di[i]*(x-Xi[i])*(x-Xi[i]);
}
void main()
{
clrscr();
float Ti=0;
A=-1,B=1;
n=26;
h=float(B-A)/n;
for(int i=0;i<=n;i++)
{
Xi[i] = A+i*h;
Yi[i] = fn(Xi[i]);
}
for(i=0;i<=n;i++)
Ai[i]=Yi[i];
Alpha[1] = 0;
Betta[1] = 0;
for(i=1;i<=n-1;i++)
{
Alpha[i+1] = (-1)/(4+Alpha[i]);
Ti = 3*(Yi[i+1]-2*Yi[i]+Yi[i-1])/(h*h) ;
Betta[i+1] = (Ti-Betta[i])/(4+Alpha[i]);
}
Ci[n]=0;
for(i=n-1;i>=0;i--) { Ci[i] = Alpha[i+1]*Ci[i+1]+Betta[i+1]; }
for(i=0;i<=n-1;i++)
{
Bi[i] = ((Yi[i+1]-Yi[i])/h)-(h*(Ci[i+1]+2*Ci[i])/3);
Di[i] = (Ci[i+1]-Ci[i])/(3*h);
}
Bi[n] = Bi[n-1]+2*Ci[n-1]*h+3*Di[n-1]*h*h;
Di[n] = Di[n-1];
printf ("Interpoliacionnaia tablica\n");
printf ("\t x f(x) s(x)\n");
for(i=0;i<=n;i++)
{
printf ("\t% .3f%12f%12f\n", Xi[i], Yi[i], Sx(Xi[i]));
}
float hp,N1=0,M1=0;
int K=100;
float xx[100],yy[100],zz[100];
hp=(B-A)/K;
for (i=0; i<K; i++)
{
xx[i] =A+i*hp;
yy[i] = fn(xx[i]);
}
for (i=0; i<K; i++)
zz[i] = Sx(xx[i]);
for(i=0;i<K;i++)
{
N1=fabs(yy[i]-zz[i]);
if(N1>M1) M1=N1;
}
printf("\P1:%f",M1);
double N2=0,M2=0;
for (i=0; i<K; i++)
{
xx[i] =A+i*hp;
yy[i] = fn(xx[i]);
}
for (i=0; i<K; i++)
zz[i] = Sx(xx[i]);
for(i=0;i<K;i++)
{
N2+=pow((yy[i]-zz[i]),2);
}
M2=sqrt(1.0/(K+1)*N2);
printf("\nP2:%2f",M2);
}
Статистические данные исходной программы(5(1).срр)
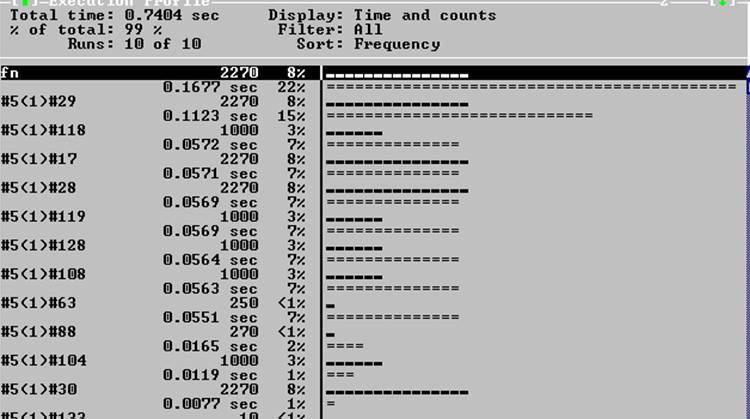
Рис. 1
Окно Файлы

Рис.2
По данным статистики, программа тратит больше всего времени на следующие области(рис.1):
Fn функция
#5(1)#29 return
#5(1)#118 xx[i]=A+i*hp
#5(1)#17 выход из функции
#5(1)#28 i=int((x-A)/h)
#5(1)#119 yy[i]=fn(xx[i])
#5(1)#128 N2+=pow(yy[i]-zz[i],2)
#5(1)#108 N1=fabs(yy[i]-zz[i])
#5(1)#63 Alpha[i+1]=(-1)/(4+Alpha[i])
#5(1)#88 printf()
#5(1)#133 выход из программы
Со строчками #5(1)#29, #5(1)#17, #5(1)#133 сделать ничего не возможно.
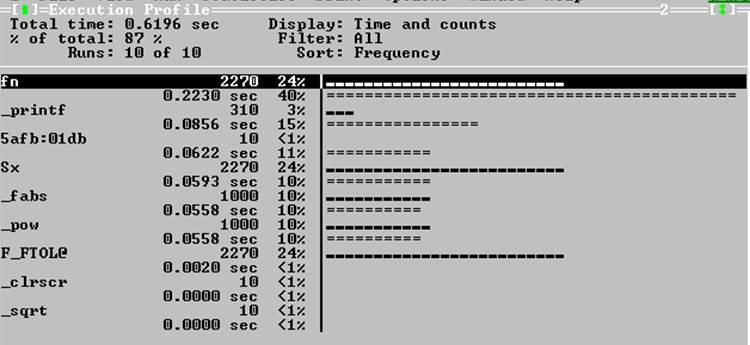
Рис. 3
Анализируя данные по функциям (рис. 3), мы видим, что основное время затрачивается на функцию fn(). К сожалению, с ней сделать ничего нельзя. На втором месте по временным затратам идет функция printf(). Так что начнем изменения с потоков ввода/вывода.
Первое изменение:
Исходные строки Преобразованные строки
Printf(“Interpoliacionnaia tablica\n”) cout<<” Interpoliacionnaia tablica\n”
Printf(“\t x f(x) s(x)\n”) cout<<” \t x f(x) s(x)\n”
Printf(“\t% .3f%12f%12f\n", Xi[i], Yi[i], Sx(Xi[i])) cout<<” "\t\n"<<Xi[i]<<Yi[i]<<Sx(Xi[i])”
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.