Использование методов приращений, построение алгоритмов и разработка программы для генерации точек кривой

Министерство образования и науки РФ

ГОУВПО «Комсомольский-на-Амуре государственный технический университет»

Кафедра МОП ЭВМ

Лабораторная работа №3

По дисциплине «Компьютерная графика»

Выполнил: Николусь П.А.

Группа: 4ВС-1

Проверила: Михайлова Н.Н.

Комсомольск-на-Амуре

2006

Вариант 14

Задание. Используя метод приращений, построить алгоритм и разработать программу для генерации точек кривой  x² + y² = R², принадлежащих второй четверти.

Уравнение окружности x² + y² = R² запишем в виде f(х,у)=x² + y² - R² = 0. Выбираем начальную точку х₀ = - R, у₀ = 0. Направление движения вдоль кривой – по часовой стрелки. В этом случае, сначала выводится отрезок кривой, для которого вектор касательной принадлежит второй октанте, а затем отрезок, для которого вектор касательной принадлежит первой октанте.

Градиент функции: .

Вектор касательной равен V=(2y, -2x).

Вектор касательной принадлежит второй октанте, если ½V_y½>½V_x½: ½-2x½>½2y½. Учитывая, что x<0 и y>0, так как они принадлежат второй четверти, получаем условие y<-x. Если  вектор касательной принадлежит второй октанте, то возможны два перемещения

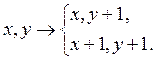
Вычислим соответствующие приращения функции f(х,у)

f(х,у₊₁)- f(х,у)    = x²+y²+2y+1-x²-y² = 2y+1>0,

f(х+1,у+1)- f(х,у)= x²+2x+1+y²+2y+1-x²-y² = 2x+2y+2<0.

Вектор касательной принадлежит первой октанте, если ½V_y½>0: ½-2x½>0. Учитывая, что x<0, получаем условие x<0. Если  вектор касательной принадлежит второй октанте, то возможны два перемещения

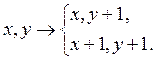
Вычислим соответствующие приращения функции f(х,у)

f(х+1,у)- f(х,у)= x² +2x+1+y²-x²-y² = 2x+1<0,

f(х+1,у+1)- f(х,у)= x²+2x+1+y²+2y+1-x²-y² = 2x+2y+2>0.

Листинг программы:

float Rad = 50;

int minxOx = -50, maxxOx = 1, minyOy = -1, maxyOy = 51;

void OnChange(TEdit *Edit, float &par);

void __fastcall TForm1::ReSize(TObject *Sender)

{

TCanvas *DC = Form1->Canvas;

int maxX = Form1->ClientWidth, maxY = Form1->ClientHeight;

TRect rect;

rect.left = 0;

rect.right = maxX;

rect.top = 0;

rect.bottom = maxY;

DC->FillRect(rect);

DC->Pen->Color = RGB(0,0,0);

DC->Pen->Width = 1;

DC->MoveTo(0, maxY * (maxyOy + 1) /(maxyOy - minyOy + 2));

DC->LineTo(maxX, maxY * (maxyOy + 1) /(maxyOy - minyOy + 2));

DC->LineTo(maxX-15, maxY * (maxyOy + 1) /(maxyOy - minyOy + 2) + 5);

DC->MoveTo(maxX, maxY * (maxyOy + 1) /(maxyOy - minyOy + 2));

DC->LineTo(maxX-15, maxY * (maxyOy + 1) /(maxyOy - minyOy + 2) - 5);

DC->MoveTo(maxX * (-minxOx + 1) /(maxxOx - minxOx + 2), maxY);

DC->LineTo(maxX * (-minxOx + 1) /(maxxOx - minxOx + 2), 0);

DC->LineTo(maxX * (-minxOx + 1) /(maxxOx - minxOx + 2) - 5, 15);

DC->MoveTo(maxX * (-minxOx + 1) /(maxxOx - minxOx + 2), 0);

DC->LineTo(maxX * (-minxOx + 1) /(maxxOx - minxOx + 2) + 5, 15);

DC->Font->Size = 10;

char str[4];

for (int i = minxOx; i < maxxOx; i += 2)

{

sprintf(str, "%d", i);

DC->TextOut((i - minxOx + 1) * maxX / (maxxOx - minxOx + 2), maxY * (maxyOy + 1) / (maxyOy - minyOy + 2) + 1, str);

DC->MoveTo((i - minxOx + 1) * maxX / (maxxOx - minxOx + 2), maxY * (maxyOy + 1) / (maxyOy - minyOy + 2) + 5);

DC->LineTo((i - minxOx + 1) * maxX / (maxxOx - minxOx + 2), maxY * (maxyOy + 1) / (maxyOy - minyOy + 2) - 5);

}

for (int i = minyOy + 1; i <= maxyOy; i += 2)

{

sprintf(str, "%d", maxyOy + minyOy - i );

DC->TextOut(maxX * (-minxOx + 1) /(maxxOx - minxOx + 2) + 4, (i - minyOy + 1) * maxY / (maxyOy - minyOy + 2) + 1, str);

DC->MoveTo(maxX * (-minxOx + 1) /(maxxOx - minxOx + 2) - 5, (i - minyOy + 1) * maxY / (maxyOy - minyOy + 2));

DC->LineTo(maxX * (-minxOx + 1) /(maxxOx - minxOx + 2) + 5, (i - minyOy + 1) * maxY / (maxyOy - minyOy + 2));

}

DC->Pen->Width = 10;

int x = -Rad, y = 0;

float df = 0;

while (y < - x)

{

DC->MoveTo(maxX * (x - minxOx + 1) / (maxxOx - minxOx + 2), maxY * (maxyOy - y + 1) / (maxyOy - minyOy + 2));

DC->LineTo(maxX * (x - minxOx + 1) / (maxxOx - minxOx + 2), maxY * (maxyOy - y + 1) / (maxyOy - minyOy + 2));

if (df <= 0)

{

df += 2 * y + 1;

}

else

{

df += 2 * x + 2 * y + 2;

++x;

}

++y;

}

while (x <= 0)

{

DC->MoveTo(maxX * (x - minxOx + 1) / (maxxOx - minxOx + 2), maxY * (maxyOy - y + 1) / (maxyOy - minyOy + 2));

DC->LineTo(maxX * (x - minxOx + 1) / (maxxOx - minxOx + 2), maxY * (maxyOy - y + 1) / (maxyOy - minyOy + 2));

if (df < 0)

{

df += 2 * x + 2 * y + 2;

++y;

}

else

{

df += 2 * x + 1;

}

++x;

}

Form1->Canvas->Font->Size = 15;

Form1->Canvas->TextOut(100,0, "y^2 + x^2 = R^2");

Form1->Label1->Refresh();

Form1->Label2->Refresh();

Form1->Label3->Refresh();

Form1->Label4->Refresh();

Form1->Label5->Refresh();

}

//--------------------------------------------------------------------------void __fastcall TForm1::ChangeR(TObject *Sender)

{

if (Form1->R->Text != "")

{

Rad = StrToFloat(Form1->R->Text);

Form1->R->Text = Rad;

}

else

Rad = 0;

ReSize(NULL);

}

//--------------------------------------------------------------------------void __fastcall TForm1::FormCreate(TObject *Sender)

{

Form1->R->Text = Rad;

Form1->xMin->Text = minxOx;

Form1->xMax->Text = maxxOx;

Form1->yMin->Text = minyOy;

Form1->yMax->Text = maxyOy;

}

//--------------------------------------------------------------------------void __fastcall TForm1::ChangeXMin(TObject *Sender)

{

if (Form1->xMin->Text != '-' && Form1->xMin->Text != "")

minxOx = StrToInt(Form1->xMin->Text);

else

minxOx = 0;

ReSize(NULL);

}

//--------------------------------------------------------------------------void __fastcall TForm1::ChangeXMax(TObject *Sender)

{

if (Form1->xMax->Text != '-' && Form1->xMax->Text != "")

maxxOx = StrToInt(Form1->xMax->Text);

else

maxxOx = 0;

ReSize(NULL);

}

//--------------------------------------------------------------------------void __fastcall TForm1::ChangeYMin(TObject *Sender)

{

if (Form1->yMin->Text != '-' && Form1->yMin->Text != "")

minyOy = StrToInt(Form1->yMin->Text);

else

minyOy = 0;

ReSize(NULL);

}

//--------------------------------------------------------------------------void __fastcall TForm1::ChangeYMax(TObject *Sender)

{

if (Form1->yMax->Text != '-' && Form1->yMax->Text != "")

maxyOy = StrToInt(Form1->yMax->Text);

else

maxyOy = 0;

ReSize(NULL);

}

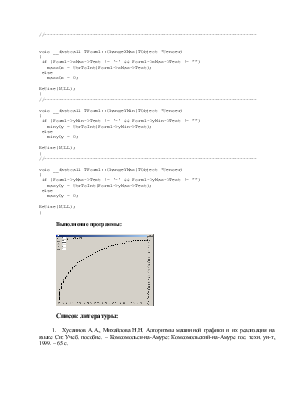
Выполнение программы:

Список литературы:

1.  Хусаинов А.А., Михайлова Н.Н. Алгоритмы машинной графики и их реализация на языке Си: Учеб. пособие. – Комсомольск-на-Амуре: Комсомольский-на-Амуре гос. техн. ун-т, 1999. – 65 с.