Хаусдорфова мера и размерность

подмногообразие  (то есть -мерная поверхность в классическом смысле).

Масштабные свойства длины, площади и объема хорошо известны. При растяжении в  раз длина кривой умножается на , площадь плоской области умножается на , а объем -мерного объекта умножается на . Как можно было бы предвидеть, -мерная хаусдорфова мера изменяет масштаб с коэффициентом . Такие масштабные свойства являются фундаментальными для теории фракталов.

Масштабное свойство: Если  и , тогда

,                                                                       (12.5)

где , т.е. множество  масштабируется с коэффициентом .

Доказательство. Если  является -покрытием , тогда  является -покрытием . Следовательно, , так как это справедливо для любого -покрытия . Переход  дает . Замена  на  и  на  дает неравенство, противоположное требуемому.

Подобный факт дает следующую основную оценку на хаусдорфовы меры множеств при действии более общих преобразований.

Утверждение 12.1. Пусть  и отображение  такое, что

       ()                                          (12.6)

для постоянных  и . Тогда для каждого

.                                                  (12.7)

Доказательство. Если  -покрытие , тогда, так как , то  является -покрытием , где . Таким образом, , так что . Когда , то , давая (12.7).

Условие (12.6) известно как условие Гельдера с показателем ; такое условие предполагает, что  непрерывна. Особенно важным является случай , т.е.

         ().                                         (12.8)

Тогда  называется отображением Липшица и

.                                                       (12.9)

Любая дифференцируемая функция с ограниченной производной обязательно является липшицевой по теореме о среднем значении. Если  является изометрией, то есть , тогда . В частности, хаусдорфовы меры инвариантны относительно переноса (то есть , где ), и инвариантны относительно вращения, как конечно можно было бы ожидать.

12.2. Хаусдорфова размерность

Возвращаясь к формуле (12.1), становится понятно, что для любого данного множества  и  , является невозрастающей с , так что, согласно (12.2),  также невозрастающая. Фактически верно следующее: если  и  – -покрытие , имеем:

;                                                           (12.10)

так что, переходя к точным верхним граням, получаем . Когда , то если , тогда  для . Таким образом, график  от  (рис. 12.1) показывает, что существует критическое значение , при котором  «прыгает» от  до . Это критическое значение называется хаусдорфовой размерностью  и записывается . (Заметим, что некоторые авторы ссылаются на хаусдорфову размерность как на размерность Хаусдорфа-Безиковича). Формально

,               (12.11)

так что

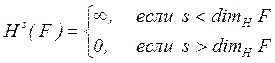.                                                  (12.12)

Если , тогда  может быть нуль или бесконечность, или может удовлетворять неравенству .

Борелевское множество, удовлетворяющее последнему условию, называется -множеством. Математически -множества являются наиболее удобными множествами для изучения, и, к счастью, они встречаются удивительно часто.

Рассмотрим простой пример. Пусть  – плоский диск единичного радиуса в . Из сходных свойств длины, площади и объема следует: ,  и . Таким образом,  с , если , и , если .

Хаусдорфова размерность удовлетворяет следующим свойствам (которые, как можно было бы ожидать, будут справедливы для любого подходящего определения размерности).

12.2.1. Открытые множества

Если  открытое, тогда , так как  содержит шар положительного -мерного объема.

Рис. 12.1

12.2.2. Гладкие множества

Если  гладкое (т.е. непрерывно дифференцируемое) -мерное подмногообразие (т.е. -мерная поверхность) из , тогда . В частности, гладкие кривые имеют размерность , а гладкие поверхности имеют размерность . Существенно, что это может быть выведено из соотношения между хаусдорфовой и лебеговой мерами.

12.2.3. Монотонность

Если , тогда . Это непосредственно следует из свойства меры, ибо  для каждого .

12.2.4. Счетная устойчивость

Если  – (счетная) последовательность множеств, тогда 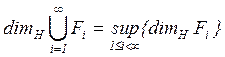. Конечно,  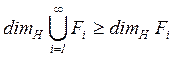для каждого  из свойства монотонности. С другой стороны, если , для всех , тогда , так что 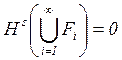. Это дает противоположное неравенство.

12.2.5. Счетные множества

Если  счетное множество, тогда . Если  единственная точка,  и , так что по счетной устойчивости .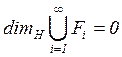

Свойства преобразования хаусдорфовой размерности следуют непосредственно из соответствующих свойств хаусдорфовых мер, данных в утверждении 12.1.

Утверждение 12.2. Пусть  и допустим, что  удовлетворяет  условию Гельдера:  (). Тогда .

Доказательство. Если , тогда, по утверждению 12.1, . Это означает, что  для всех .

Следствие 12.1.

(a)  Если  – липшицево преобразование (см. (12.8)), тогда .

(b)  Если  би-липшицево преобразование, т.е.:

  (),                             (12.13)

где , тогда .

Доказательство. Пункт (а) следует из утверждения 12.2, если взять . Применение этого пункта к обратному преобразованию  дает другое неравенство. Это доказывает пункт (b).

Следствие 12.1обнаруживает фундаментальное свойство хаусдорфовой размерности: Хаусдорфова размерность инвариантна относительно би-липшицевого преобразования. Таким образом, если два множества имеют разные размерности, то не может быть би-липшицева отображения из одного множества в другое. Это напоминает ситуацию в топологии, где различные «инварианты» (такие как группы гомологии или гомотопии) используются для различия множеств, которые не являются гомеоморфными: если топологические инварианты двух множеств различны, тогда не может быть гомеоморфизма (непрерывного взаимнооднозначного отображения с непрерывным обратным) между этими множествами.

В топологии два множества рассматриваются как «одинаковые», если существует гомеоморфизм между ними. Один из подходов к фрактальной геометрии – рассматривать два множества как «одинаковые», если существует би-липшицево отображение между ними. Топологические инварианты используются лишь для различения между негомеоморфными множествами. Однако мы можем найти другие параметры, включая хаусдорфову размерность, чтобы провести различия между множествами, которые не являются би-липшицево эквивалентными. Так как би-липшицевы преобразования (12.13) обязательно непрерывны, то топологические инварианты могут использоваться в этом направлении, а хаусдорфова