Интерполяция функций. Использование метода Рунге-Кутта четвертого порядка и метод Милна

Министерство образования Российской Федерации

Комсомольский-на-Амуре государственный

технический университет

Факультет компьютерных технологий

Кафедра МОПЭВМ

Расчетно-графическое задание №1.

«Интерполяция функций».

Вариант 20.

Выполнил: Шелестов И.А.

Группа: 4ВС-1

Проверила: Михайлова Н.Н.

Комсомольск-на-Амуре

2006

Задание:

Используя метод Рунге-Кутта четвертого порядка и метод Милна, составить таблицу приближенных значении интеграла дифференциального уравнения y'=f(x,y), удовлетворяющего начальному условию у(0)=1, на отрезке [0,1], шаг h=0.05. В методе Милна начальный отрезок определить методом Рунге-Кутта четвертого порядка, выдать на печать значения погрешности. Для сравнения вызвать библиотечную функцию. Проверить результат, вычислив значения точного решения. Найти дискретные аналоги точного и приближенного решений. Построить графики точного и приближенных решений.

Заданная функция:

.

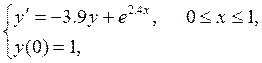
Формула точного решения

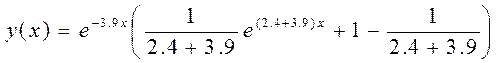
Алгоритм решения.

Запишем задачу Коши в виде:

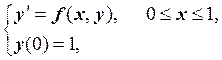
Известно, что задача Коши имеет единственное решение, если || £ M,   M > 0.   В нашем случае  = – 3.9,   M = 3.9.  Условие выполнено, следовательно, задача Коши имеет единственное решение.

Запишем алгоритм метода Рунге-Кутта четвертого порядка:

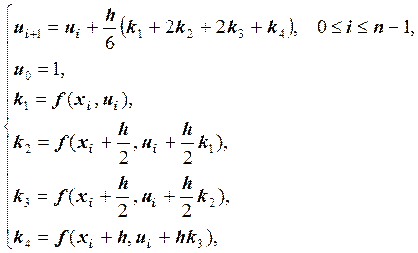
где  h = 0.05,              n = 1/h = 10,              x_i,

.

Приближенным решением является сеточная функция: u = (u0, u1, u2, … u10).

Листинг программы.

//Подключаемые библиотеки

#include <conio.h>

#include <math.h>

#include <stdio.h>

#include<graphics.h>

/*   Глобальные переменные и массивы:

n - число узлов сетки

x[n] - массив узлов сетки

y[n] - массив значений точного решения

u[n] - массив значений приближенного решения

h - шаг сетки

m,k - параметры, входящие в формулу точного решения

K1,K2,K3,K4 - коэффициенты метода Рунге-Кутта

*/

const int n = 1/0.05+2;

double x[n], y[n], u[n], h = 0.05, s[n], u1[n],

m = 3.9, k = 2.4, K1, K2, K3, K4;

float xmin=0, xmax=1;                  // Область изменения x

float ymin=-2, ymax=2;                  // Область изменения y

float hx;                          // Шаг

float xdens, ydens;

// Вычисление экранной x координаты

int ex(float x,float y)

{return (int) ((x-xmin)/xdens);}

// Вычисление экранной y координаты

int ey(float x,float y)

{return (int) ((ymax-y)/ydens);}

// возвращает значение функции (правой части ДУ)

double f (double x,double y) { return -m*y+exp(k*x); }

//Вычисление дискретных аналогов

void diskr_analog(int m)

{

double sum=0,max=0,p;

int i;

if(m==1)

{

for(i=0;i<n;i++)

{

p=u[i]-y[i];

if(fabs(p)>max) max=fabs(p);

sum+=pow(p,2);

}

printf("\nДискретный аналог: р1=%lf",max);

printf("\nДискретный аналог: р2=%lf",pow(sum/(n+1),0.5));

}

else

{

for(i=0;i<n;i++)

{

p=u[i]-y[i];

if(fabs(p)>max) max=fabs(p);

sum+=pow(p,2);

}

printf("\nДискретный аналог: р1=%lf",max);

printf("\nДискретный аналог: р2=%lf",pow(sum/(n+1),0.5));

}

}

void graf()

{int graphdriver= DETECT, graphmode;

float xx,yy;

// Инициализация графического режима:

initgraph(&graphdriver,&graphmode,"C:\\BORLANDC\\BGI");

xdens=(xmax-xmin)/getmaxx(); //Вычисление коэффициента масштабирования по x

ydens=(ymax-ymin)/getmaxy(); //Вычисление коэффициента масштабирования по y

int i=0;

setcolor(WHITE);

for(xx=xmin;xx<=xmax-h;xx+=h)

{

line(ex(xx,y[i]),ey(xx,y[i]), ex(xx+h, y[i]+h), ey(xx+h, y[i]+h));

i++;};

getch();

setcolor(RED);

i=0;

for(xx=xmin;xx<=xmax-h;xx+=h)

{line(ex(xx,u[i]),ey(xx,u[i]), ex(xx+h,u[i]+h), ey(xx+h,u[i]+h));

i++;};

getch();

closegraph (); // Выход из графического режима

}

void main (void)

{

clrscr ();

printf("\n\t\tЧисленное решение задачи Коши для обыкновенных\n\

\tдифференциальных уравнений первого порядка");

// Метод Рунге-Кутта четвертого порядка

for(int i=0; i<n; i++)

{

double a = i*h; x[i] = a;

// формула точного решения

y[i] = (exp((k+m)*a)/(k+m)+1-1/(k+m))/exp(m*a);

}

u[0] = 1;

for(i=0; i<n-1; i++)

{

K1=f(x[i], u[i]);

K2=f(x[i]+h/2, u[i]+h/2*K1);

K3=f(x[i]+h/2, u[i]+h/2*K2);

K4=f(x[i]+h, u[i]+h*K3);

// вычисление приближенного решения

u[i+1] = u[i]+h/6*(K1+2*K2+2*K3+K4);

}

// Вывод результатов на экран

printf("\n\nМетод Рунге-Кутта");

printf ("\n\n\tРезультаты расчета:\n");

printf ("\nУзлы сетки\tТочное решение\tПриближенное решение\n");

for (i=0; i<n; i++)

{

printf ("\n%10.2f\t% -14.4f\t% -20.4f\t", x[i], y[i], u[i]);

}

diskr_analog(1);

printf("\nДля продолжения нажмите любую клавишу...");

getch();

graf();

//Метод Милна

for(i=3;i<=(n-1);i++)

{

s[i+1]=u[i-3]+(4*h/3)*(2*f(x[i-2],u[i-2])f(x[i-1],u[i-1])+2*f(x[i],u[i]));

u[i+1]=u[i-1]+(h/3)*(f(x[i-1],u[i-1])+

4*f(x[i],u[i])+f(x[i+1],s[i+1]));

}

clrscr();

printf("\n\n\nМетод Милна.");

printf ("\n\n\tРезультаты расчета:\n");

printf ("\nУзлы сетки\tТочное решение\tПриближенное решение\n");

diskr_analog(2);

for (i=0; i<n; i++)

{

printf ("\n%10.2f\t% -14.4f\t% -20.4f\t", x[i], y[i], u[i]);

}

getch();

graf();

}

Результат работы программы.

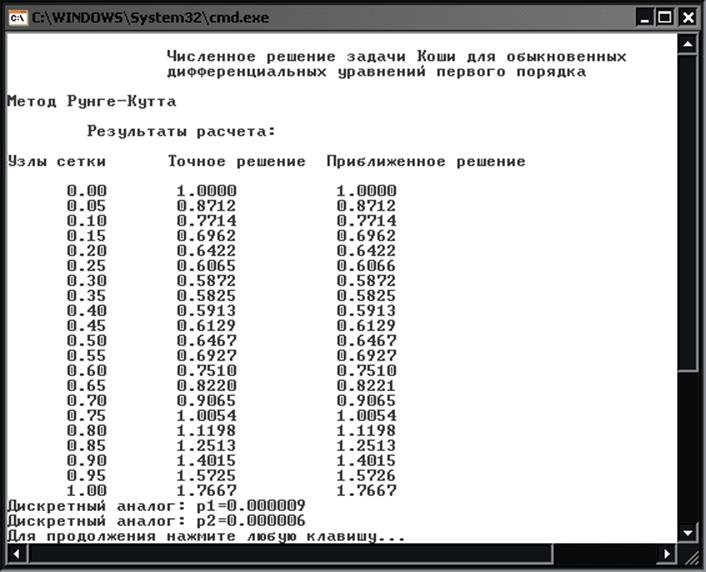
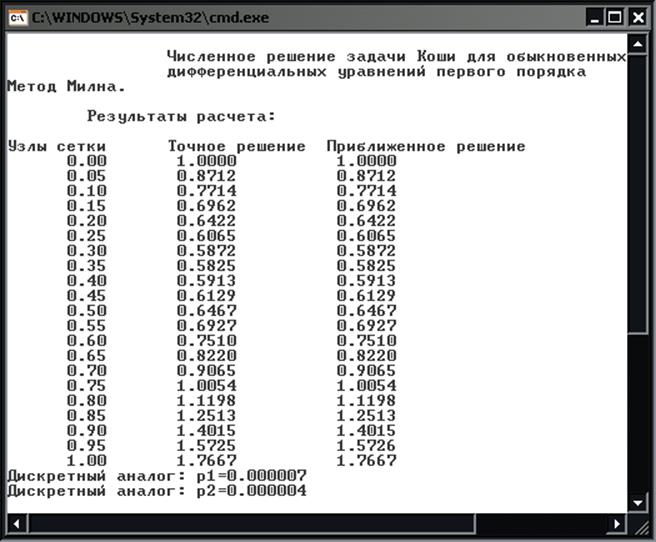
Графики: