Расчет системы автоматического управления тяговыми электродвигателями электровозов переменного тока: Учебное пособие, страница 3

Регулировочная и нагрузочная характеристики выпрямительно-инверторного преобразователя определяются следующим выражением:

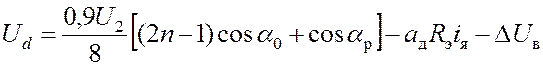.                 (2)

В выражении (2) обозначены:

      п – номер зоны регулирования (число нагруженных четвертей тяговой обмотки трансформатора);

R_э – эквивалентное сопротивление ВИП;

      α₀, α_р - фазовые углы отпирания тиристорных плеч буферного и регулируемого контуров ВИП.

      ∆U_в – потеря напряжения в тиристорных плечах ВИП.

Диаграмма выходного напряжения ВИП для второй - четвертой зон регулирования показана на рис 2.

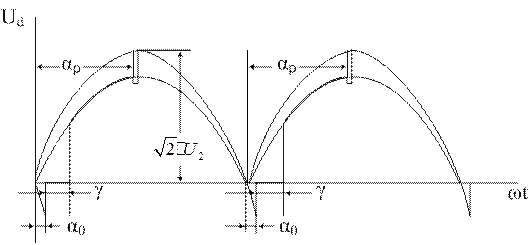
Рис.2.Диаграмма выходного напряжения ВИП

Эквивалентное сопротивление ВИП R_э учитывает потерю напряжения, обусловленную коммутацией тиристорных плеч. На интервале углов коммутации γ тяговая обмотка трансформатора находится в режиме короткого замыкания. Эквивалентное сопротивление ВИП рассчитывают по формуле:

                     .                                     (3).

Регулировочная характеристика ВИП имеет нелинейную зависимость выходного напряжения от угла регулирования  α_р.  Для определения коэффициентов усиления исполнительного устройства надо выполнить линеаризацию его характеристики. С этой целью нелинейную зависимость характеристики ВИП от угла регулирования α_р надо заменить линейным отрезком и рассматривать в ограниченном диапазоне пропорциональное изменение переменных Du₂, Di_я, Dα_р  относительно постоянных величин  U₂, I_я, α_р.

.                                         

Коэффициенты линеаризации характеристики ВИП (коэффициенты усиления) определяют аналитически, методом частного дифференцирования формулы (2) по напряжению u₂ и по углу фазового регулирования  α_р:

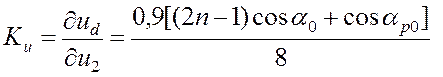;            (4)

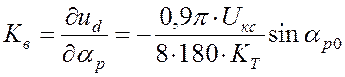, [В/град].     (5)

Линеаризованное уравнение изменения выходного напряжения ВИП в операторной форме получено путем преобразования выражений (1) и(2):

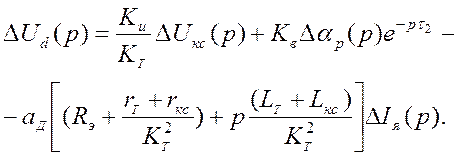                        (6)

Уравнение (6) содержит звено запаздывания передачи сигнала по углу фазового регулирования ВИП с постоянной запаздывания .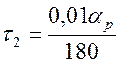

Форсирующее звено, выделенное в уравнении (4) прямыми скобками, учитывает влияние индуктивности обмоток тягового трансформатора. В дальнейших преобразованиях параметры этого звена объединены с параметрами звена цепи якоря в уравнении цепи ТЭД.

                     3.2. Динамические характеристики объекта регулирования

Динамические характеристики объекта регулирования определяют путем преобразования дифференциальных уравнений равновесия напряжений и э.д.с. цепи якоря, намагничивающих сил с учетом действия вихревых токов в массивных частях магнитопровода ТЭД, а также уравнение равновесия механических сил, приведенных к ободу колесной пары [2].

Уравнение для цепи якорей тяговых электродвигателей:

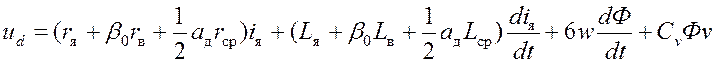.(7)

Уравнения намагничивающих сил ТЭД:

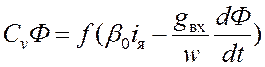                                     ,                                                  (8)

Уравнение равновесия сил, приведенных к ободу колесной пары:

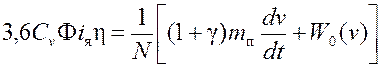                              .                      (9)

В уравнениях (7)- (9) приняты следующие обозначения:

,,,,, - соответственно суммарные величины сопротивлений и индуктивности обмоток якоря, обмоток возбуждения ТЭД, сопротивление и индуктивность сглаживающего реактора;

С_vФ- магнитный поток ТЭД с масштабным коэффициентом С_v тягового электропривода;

w – число витков полюсных катушек главных полюсов ТЭД;

β₀- коэффициент постоянного шунтирования обмоток возбуждения ТЭД;

g_вх,– проводимость контура вихревых токов ТЭД;

η – коэффициент, учитывающий снижение силы тяги за счет магнитных потерь в якоре ТЭД и механических потерь в редукторе тягового привода ;

m_п  - масса поезда, т;

N – число тяговых осей электровоза;

γ – коэффициент инерции вращающихся частей экипажной части поезда.

W₀(v) - сила сопротивления движению поезда.

Для определения динамических параметров объекта регулирования надо выполнить линеаризацию дифференциальных уравнений (7)-(8). В этих уравнениях нужно заменить на интервале ∆I_в нелинейную зависимость характеристики намагничивания С_vФ(I_в) ТЭД линеаризующим отрезком (a-b) с коэффициентом наклона К_ф (рис. 3):

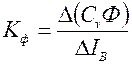                        ,                         [Ом/км/ч].                                        (10)

Пропорциональное изменение переменных Du_d, Di_я, D(С_vФ) в уравнениях (7)-(8) надо рассматривать в ограниченном диапазоне относительно постоянных величин  U_d, I_я, С_vФ. Скорость движения v_о за время протекания  переходных электромагнитных процессов можно считать практически неизменной.

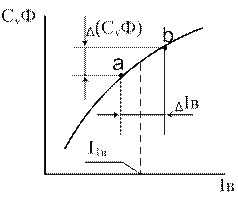
Рис.3. Линеаризация характеристики намагничивания ТЭД

Для определения передаточной функции ТЭД рассматриваются уравнения  для цепи якоря и цепи возбуждения.

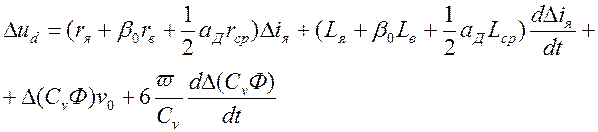;(11)

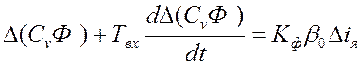                     ;                                          (12)

Для определения передаточных функций объекта регулирования надо выразить уравнения (11)-(12) в операторной форме и преобразовать относительно выходных переменных DI_я(p), D(С_vФ)(p). В уравнении (11) выходное напряжение ВИП DU_d(p) надо выразить уравнением (6):

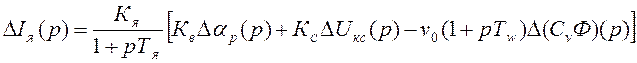;        (13)

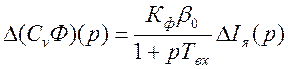                     .                                                            (14)

В уравнениях (13), (14) приняты следующие обозначения коэффициентов усиления и постоянных времени:

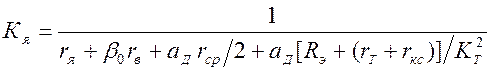      ,[1/Ом];          (15)

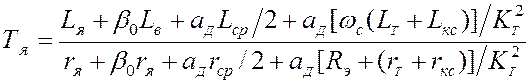       ,[с];       (16)

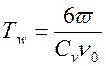                                                    , [с].                                                     (17)

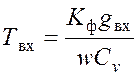,         [с];                                                     (18)

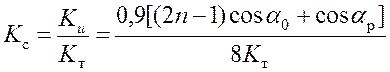.           (19)

Структурная схема ТЭД  при условии неизменной скорости движения показана на рис.4. Апериодическое звено 1-го порядка цепи якорей ТЭД охвачено обратной связью с передаточной функцией, содержащей апериодическое звено 1-го порядка контура вихревых токов магнитопровода и форсирующее звено формирования э.д.с.  обмоток якоря и возбуждения ТЭД.

Эквивалентная операторная передаточная функция ТЭД имеет следующий вид:

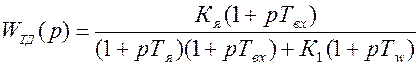                                                 (20)

Здесь К₁ – коэффициент усиления по контуру обратной связи  э.д.с. ТЭД.

                                    .                                                                                 (21)