Равномерное распределение. Двумерный центрированный гауссовский случайный вектор

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА №12

Работа защищена с оценкой

Преподаватель

доц., к.т.н.				А. В. Лопарев
должность, уч. степень, звание		подпись, дата		инициалы, фамилия
Отчет о выполнении практической работы
Задание №1.
по дисциплине: ОБРАБОТКА НАВИГАЦИОННОЙ ИНФОРМАЦИИ

РАБОТУ ВЫПОЛНИЛА

СТУДЕНТКА ГР. 1421                                                                              Н. А. Станулевич

Санкт-Петербург
2008

1.  Равномерное распределение.

Наименование распределения	Параметры распределения
Равномерное

1.1.  Вычисление математического ожидания и дисперсии при заданных параметрах.

>> a=0;

>> b=10;

>> [m,v]=unifstat(a,b)

m = 5

v =8.3333

Проверка полученных значений.

m=(a+b)*0.5=5

v=(b-a)²/12=8,(3)

1.2.  С использованием Matlab построение графиков функции плотности распределения вероятности при заданных параметрах и при их значениях, уменьшенных в два раза.

x=-5:0.01:15;

>> y=unifpdf(x,a,b);

>> plot(x,y,'--');

>> hold on;

>> y1=unifpdf(x,a*0.5,b*0.5);

>> plot(x,y1,'r');

Рис. 1. Графики функций плотности распределения вероятности.

1.3.  С использованием соответствующих m- функций Matlab получение 200 реализаций случайных величин, вычисление выборочных значений математического ожидания, дисперсии и медианы. Вычисления при числе реализаций, равном 20000, построение гистограммы.

>>r=unifrnd(0,10,200,1);

>> M=mean(r)

M =4.9690

>> med=median(r)

med =4.9743

>> d=var(r)

d =7.9224

>> hist(r);

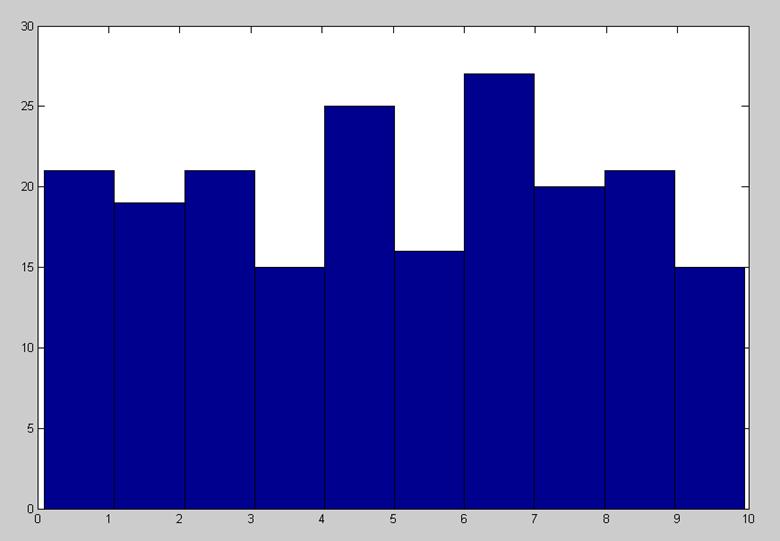
Рис. 2. Гистограмма для m=200.

>> r1=unifrnd(0,10,20000,1);

>> M1=mean(r1)

M1 =5.0301

>> med1=median(r1)

med1 =5.0593

>> d1=var(r1)

d1 =8.3864

>> hist(r1);

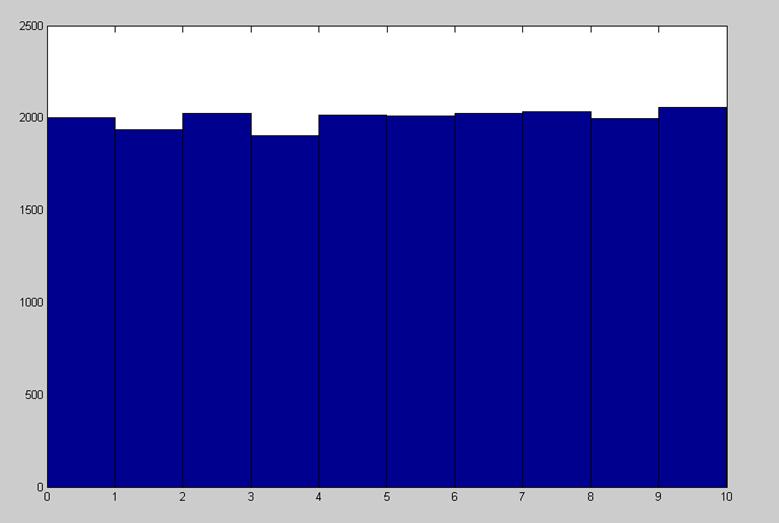
Рис. 3. Гистограмма для m=20000.

Из полученных значений видно, что вариант с 20000 реализаций по своим параметрам (математическое ожидание, дисперсия) более близок к значениям, полученным в пункте 1.1.

2.  Двумерный центрированный гауссовский случайный вектор.

N	4
	4
	-1
	1
*

2.1.  Выражение для функции плотности распределения вероятности

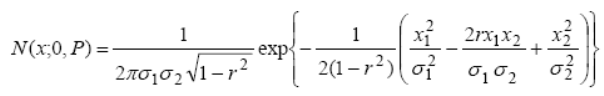
2.2.  Параметры среднеквадратического эллипса ошибок.

σ₁=(P₁₁)^1/2=2

σ₂=(P₂₂)^1/2=1

r=P₁₁/( σ₁* σ₂)= -0.5

2.3.  С помощью Matlab построение графика двумерной функции.

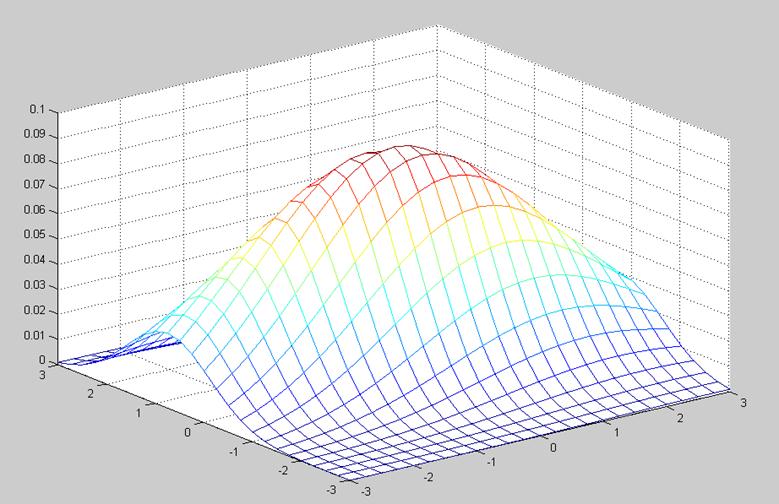
Рис. 4. График двумерной функции плотности распределения вероятности.

>> [x,y]=meshgrid([-3:0.25:3]);

>> s1=2;

>> s2=1;

>> r=-0.5;

>> z=1/(2*pi*s1*s2*sqrt(1-r^2))*exp(-1/(2*(1-r^2))*(x.^2/s1^2-2*r*x.*y./s1/s2+y.^2/s2^2));

>> mesh(x,y,z);

2.4.  Параметры и график одномерной гауссовской функции плотности распределения вероятности, для величины, определяющей проекцию центрированного гауссовского вектора на заданное в указанном варианте направление .

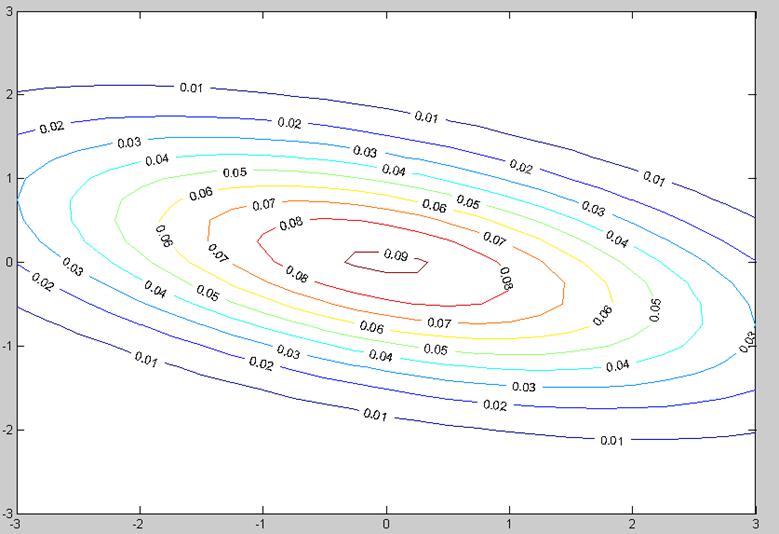
Рис. 5. График одномерной гауссовской функции плотности распределения вероятности.

>> [c,h]=contour(x,y,z);

>> clabel(c,h);

Параметры среднеквадратичного эллипса

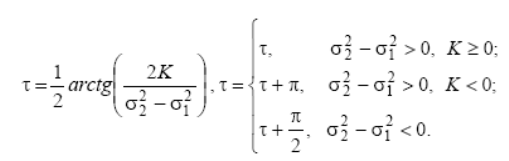
τ=106,8°

При σ₁=2, σ₂=1, К=Р₁₂= -1 найдем дисперсию по формуле

D_ρ=0.88

Тогда σ=0,94.

>> x=-2.82:0.01:2.82;

y=normpdf(x,0,0.94);

>> plot(x,y)

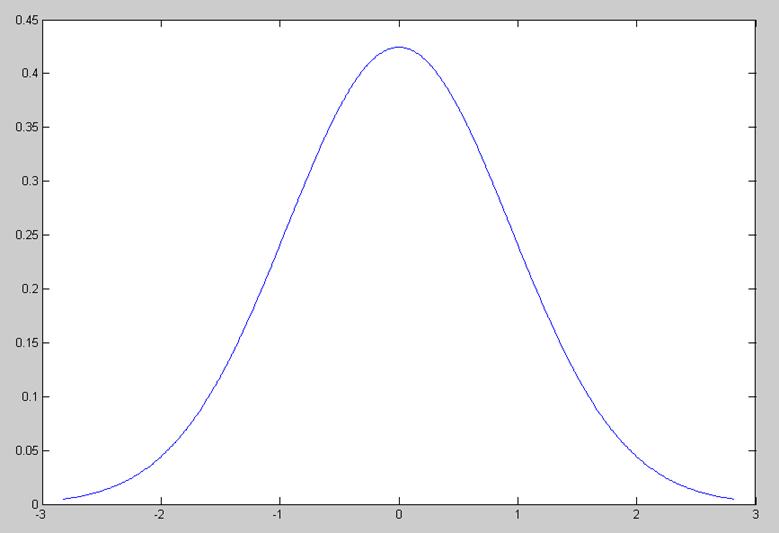
Рис. 6. Графики функций плотности распределения вероятности.

Примечание. Элемент  - определяет дисперсию для вертикальной координаты, а  - для горизонтальной координаты.