Применение комбинаторных схем для построения систем связи высокой производительности и надежности, страница 2

Рассмотрим комбинацию 0 1 1 1 1 0 0, которая соответствует числу 12. Пусть при передаче символ на 5-й позиции изменился (1 перешла в 0). Искаженная кодовая комбинация стала 0 1 1 1 0 0 0. Из таблицы 2 позиции первой проверки 1, 3, 5, 7. Проверка дала нечетное число - ставим 1. Вторая проверка на позициях 2, 3, 6, 7 дала четное число – ставим 0. Третья проверка дала нечетное число – ставим 1. В итоге проверочное число 1 0 1 = 5. Следовательно, на 5-й позиции произошла ошибка. Значение на этой позиции необходимо изменить на обратное 0 ® 1.

Будем использовать коды Хэмминга при проверке на нечетность, которые исправляют одиночные ошибки, для построения системы связи. Позициям кодов сопоставим номера узлов, а числам – номера сетей. Запишем проверочную матрицу кода Хэмминга (7, 4), т.е. при n = 7, n₀ = 4, при проверке на нечетность, взяв, например, числа 6, 3, 15. В нашем случае имеем (см. таблицу 5).

Таблица 5. Коды Хэмминга для десятичных чисел (проверка на нечетность)

При использовании такой матрицы для построения системы связей между парами узлов в сети не обеспечивается прямая связь. Например, отсутствует прямая связь между узлами 1 и 2, 1 и 3 и т. д. Для преодоления этого недостатка нарастим матрицу за счет добавления новых строк, представляющих собой линейную комбинацию строк исходной матрицы.

Для обеспечения взаимосвязи узлов 1 и 2 используем линейную комбинацию строк 1 и 2; для прямой взаимосвязи узлов 1 и 3 возьмем линейную комбинацию строк 1 и 3; для прямой связи узлов 2 и 3 – линейную комбинацию строк 2 и 3 исходной матрицы. В результате получаем расширенную матрицу следующего вида (см. таблицу 6)

Таблица 6. Расширенная матрица кодов Хемминга

Здесь для каждой пары столбцов имеется не менее одной строки, на пересечении с которой эти столбцы имеют элементы равные 1. Например, для столбцов 1 и 2 такой строкой является строка 4, для столбцов 4 и 5 такими строками являются строки 1 6 и т. д.

Система связи будет содержать 6 отдельных сетей. Первая из этих сетей связи будет объединять узлы 1, 4, 5, 6. Вторая сеть связи будет объединять узлы 2, 4, 6, 7. Узел 1 одновременно подключен к сетям связи 1, 4 и 5. Узел 2 подключен к сетям связи 2, 4, 6  и  т.д. На рисунке 2 приведена структура сетей связи.

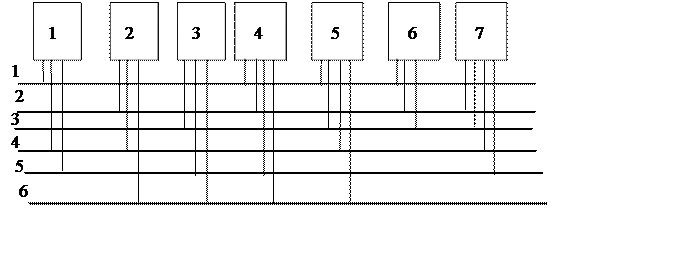Рис. 2. Полная система сетей связи (однократное соединение)

Если добавить еще одну строку, являющейся линейной комбинацией строк 1, 2 и 3, то получим структуру системы связи, обладающей отказоустойчивостью (l = 2). В этой структуре системы связи между каждой парой узлов обеспечивается связь с помощью двух сетей связи. Соответствующая матрица, использующая код Хэмминга (7,4) приведена в таблице 7.

           Таблица 7 Матрица отказоустойчивой сети

Эта матрица по своим свойствам соответствует блок-схеме с параметрами N = B =7;
 k = r = 4; l = 2. На рисунке 3 приведена структура системы связи.

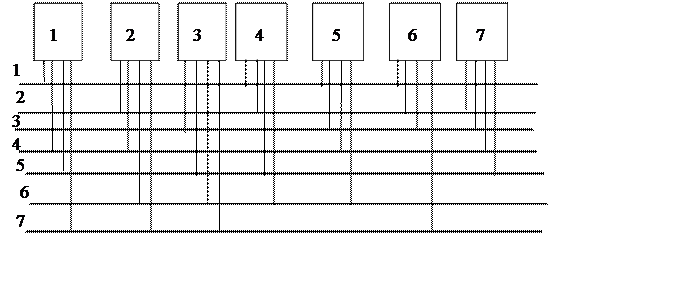Рисунок 3. Полная система сетей связи (двукратное соединение)

Рассмотрим эвристический алгоритм построения системы связи на базе проверочных матриц помехоустойчивых кодов. Алгоритм формирования матриц инциденций имеет следующий вид:

1. Выбрать очередную пару столбцов с номерами i и j, которые еще не рассматривались на предыдущих шагах.

2. Проанализировать наличие в матрице хотя бы одной строки, содержащей единицы на i-й и j-й позициях. Если такая строка имеется, то перейти к п.4. Если такой строки нет, то перейти к п.3.

3. Сформировать из линейно независимых строк матрицы новую линейную комбинацию, содержащую единицы на позициях i и j, и дополнить матрицу этой строкой.

4. Проверить, все ли коды столбцов просмотрены. Если просмотрены все, то перейти к п.1.

5. Минимизировать число УК в сетях и число соединений УК с сетями удаляя «лишние» единицы в строках и столбцах, сохранив заданное l.

Аналогичным образом осуществляется поиск матрицы для систем связи повышенной надежности (l > 1). В этом случае п.2 изложенного алгоритма связан с анализом наличия в матрице не менее l строк, содержащих элементы равные 1 на рассматриваемых столбцах.

Выбор в качестве исходной матрицы проверочной матрицы корректирующих кодов (например, кодов Хэмминга) обоснован тем, что предлагаемые матрицы хорошо структурированы, содержат линейно независимые строки, а в теории помехоустойчивого кодирования хорошо развит аппарат построения таких матриц.

Содержание отчета

1.Задание с указанием расшифровки условных обозначений переменных.

2.Краткое описание метода получения заданной системы связи.

3.Матрица и рисунок, описывающие систему сетей связи.

4.Текст проверяющей программы (с подробными комментариями). Программа должна иметь возможность изменения исходных данных.

5.Результаты экспериментов по изменению матрицы.

Варианты заданий

N	Основа построения	Тип соединения	Параметры
			N	B	k	r
1	Уравновешенные неполные блок-схемы	Односвязные(λ = 1)	4	6	2	3
5			5	10	2	4
9			9	12	3	4
13			13	13	4	4
2		Двусвязные (λ = 2)	4	4	3	3
6			6	10	3	5
10			7	7	4	4
14*			10	15	4	6
17*			11	11	5	5

N	Основа построения	Тип соединения	Исходные числа матрицы
3	Проверочные матрицы кодов Хэмминга при проверке на нечетность	Однократное (λ = 1)	5	11	13
7			5	13	14
11			3	7	13
15			0	2	13
18			3	4	9
20			4	10	11
22			7	8	12
23			3	8	12
24			6	10	11
4		Двукратное (λ = 2)	11	13	14
8			9	11	13
12			6	9	11
16			3	5	13
19			3	9	12
21			7	9	13

Примечание. *-усложненный вариант.