ПРИМЕНЕНИЕ КОМБИНАТОРНЫХ СХЕМ ДЛЯ ПОСТРОЕНИЯ
СИСТЕМ СВЯЗИ ВЫСОКОЙ ПРОИЗВОДИТЕЛЬНОСТИ
И НАДЕЖНОСТИ
Цель работы - ознакомление с методами построения высокопроизводительных и высоконадежных систем связи на основе уравновешенных неполных блок-схем и структур корректирующих кодов.
Теоретические пояснения.
В некоторых случаях необходимо обеспечить возможность передачи пакетов без их коммутации в промежуточных узлах. В таком случае каждый узел за счет выбора одной из сетей связи, к которой он подключен, должен быть соединен с любым другим узлом. Для построении таких сетей связи возможны два подхода: использование уравновешенных неполных блок-схем и применение структур корректирующих кодов.
Рассмотрим эти подходы.
В нашем случае уравновешенной неполной блок-схемой (сокращенно блок-схемой) называется такое размещение N различных узлов по B сетям связи, при котором каждая сеть содержит точно k различных узлов, каждый узел появляется точно в r различных сетях и каждая пара различных узлов ai и aj появляется точно в l сетях. При этом блок-схемы обладают следующими свойствами Bk = Nr, r(k-1) = l(N-1), B ³ N, r ³ k.
Таким образом, количество объединяемых сетей связи всегда не менее числа узлов, а каждый узел подключен к такому числу сетей связи, которое не меньше числа узлов в отдельной сети.
В качестве примера рассмотрим односвязную систему связи с параметрами
N = B = 7; r = k =3; l = 1. В этом случае блок-схема описывается следующей матрицей инциденций (таблица 1).
Таблица 1. Матрица инциденций
|
B (сети) |
N (узлы) |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
1 |
1 |
1 |
||||
|
2 |
1 |
1 |
1 |
||||
|
3 |
1 |
1 |
1 |
||||
|
4 |
1 |
1 |
1 |
||||
|
5 |
1 |
1 |
1 |
||||
|
6 |
1 |
1 |
1 |
||||
|
7 |
1 |
1 |
1 |
||||
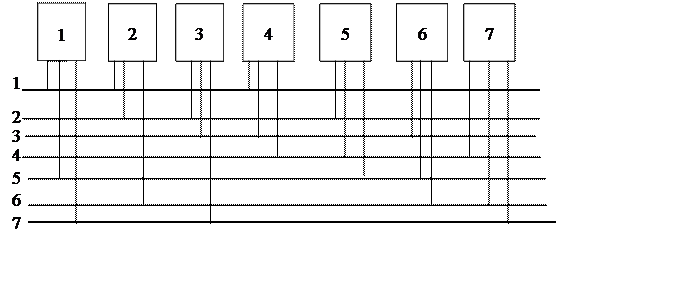
Эту матрицу можно интерпретировать следующим образом. Каждая строка соответствует одной сети связи, которая содержит 3 узла с номерами, равными номерам тех столбцов, которые содержат 1. Например, сеть 1 включает узлы с номерами 1, 2, 4, а сеть 2 содержит узлы с номерами 2, 3, 5. Узел 1 имеет прямую связь c узлами 2 и 4 через сеть 1, узел 1 имеет прямую связь с узлами 5 и 6 через сеть 5 и узлами 3 и 7 через сеть связи 7.
Данную систему сетей связи можно записать путем перечисления номеров узлов, которые входят в частные сети связи (таблица 2).
Таблица 2. Номера узлов в сетях связи
|
Номер сети связи |
Номер узла |
||
|
1 |
1 |
2 |
4 |
|
2 |
2 |
3 |
5 |
|
3 |
3 |
4 |
6 |
|
4 |
4 |
5 |
7 |
|
5 |
1 |
5 |
6 |
|
6 |
2 |
6 |
7 |
|
7 |
1 |
3 |
7 |
![]()
|
 |
Теперь рассмотрим построение структуры системы связи за счет расширения проверочной матрицы кода Хэмминга. Коды Хэмминга широко используются при передаче информации. Суть их заключается в следующем.
Пусть из общего числа позиций n для передачи информации используется n0 позиций, которое будем считать фиксированным. Остальные позиции, число которых k < n0 используются в качестве проверочных. Символы, которые ставятся на k проверочных позициях, определяются при кодировании проверкой на четность или нечетность каждой из k групп информационных позиций.
При проверке на четность на каждой проверочной позиции при кодировании ставится 0 или 1, смотря по тому, какая сумма единиц четная или нечетная, получается при сложении проверяемых позиций, соответствующих данной проверочной позиции. Сигнал кодируется так, чтобы в результате в каждой из k проверок получалось четное число. При приеме также производится проверка на четность.
Построим код, который позволял бы
обнаруживать и исправлять одиночную ошибку. Пусть принята кодовая комбинация с
ошибкой или без ошибки. Произведем в ней последовательно k проверок,
после каждой проверки запишем 0, если результат свидетельствует об отсутствии
ошибки на проверяемых позициях (сумма единиц четная). Запись справа налево
полученной последовательности единиц и нулей дает двоичное число. Это число
называется проверочным. Потребуем, чтобы оно давало номер позиции, по которой
произошло искажение. Проверочное число должно описывать (n0 +
k + 1) событий. Следовательно, число k определяется на основании
неравенства 2k ³ n0
+ k + 1 или 2n-n0 ³ n +1 или 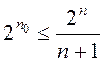 . Это соотношение
позволяет определить максимальное n0 при данном n или
минимальное n для данного n0.
. Это соотношение
позволяет определить максимальное n0 при данном n или
минимальное n для данного n0.
Выбор для проверки позиций 1, 2, 4, 8, обеспечивает появление хотя бы одной из этих позиций при каждой проверке, что позволяет независимо от значения посылаемого числа получить при каждой проверке четное число единиц. Соответствующие проверяемые позиции для каждой проверочной позиции приведены в таблице 3.
Таблица 3. Соответствие проверочных и проверяемых позиций
|
Порядковый номер |
Проверочные позиции |
Проверяемые позиции |
|
1 |
1 |
1, 3, 5, 7, 9, 11, 13, 15, 17,… |
|
2 |
2 |
2, 3, 6, 7, 10, 11, 14, 15, 18,… |
|
3 |
4 |
4, 5, 6, 7, 12, 13, 14, 15, 20,… |
|
4 |
8 |
8, 9, 10, 11,12, 13, 14, 15, 25,… |
Для примера рассмотрим код Хэмминга для n = 7. Согласно вышеприведенному соотношению n0 = 4, k = 3. Позиции 1, 2, 4 будут использованы для передачи проверочных символов. На остальных позициях разместим двоичные представления чисел от 0 до 15. Подобные комбинации приведены в таблице 4.
Таблица 4. Коды Хэмминга для десятичных чисел (проверка на четность)
Позиция |
Десятичное представление двоичных чисел, образовавших символы на позициях 3, 5, 6, 7 |
|
1 2 3 4 5 6 7 |
|
|
0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 1 0 1 0 1 0 1 0 0 0 0 1 1 1 0 0 1 1 0 0 0 1 0 0 1 0 1 1 1 0 0 1 1 0 0 0 0 1 1 1 1 … 0 1 1 1 1 0 0 |
0 1 2 3 4 5 6 7 … 12 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.