

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА №12
Работа защищена с оценкой
Преподаватель
|
доц., к.т.н. |
А. В. Лопарев |
||||
|
должность, уч. степень, звание |
подпись, дата |
инициалы, фамилия |
|||
|
Отчет о выполнении практической работы |
|||||
|
Задание №2. |
|||||
|
по дисциплине: ОБРАБОТКА НАВИГАЦИОННОЙ ИНФОРМАЦИИ «оценивание коэффициентов полинома» |
|||||
РАБОТУ ВЫПОЛНИЛА
СТУДЕНТКА ГР. 1421 Сивкина М.И.
Санкт-Петербург
2008
1.Цель работы.
Изучить методы оценивания коэффициентов полинома, сравнить полученные с помощью разных методов оценки.
Начальные
данные: ![]() ,
,![]() -моделируемое измерение.
-моделируемое измерение.
здесь ![]() ,
, ![]() - независимые между собой,
центрированные гауссовские случайные величины с дисперсиями
- независимые между собой,
центрированные гауссовские случайные величины с дисперсиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() -
независимые между собой и от
-
независимые между собой и от ![]() ,
, ![]() , центрированные гауссовские
случайные величины с дисперсиями
, центрированные гауссовские
случайные величины с дисперсиями ![]() ,
, ![]() ;
; ![]() ,
, ![]() , - время от начала наблюдения;
, - время от начала наблюдения; ![]() - интервал проведения измерений,
- интервал проведения измерений, ![]() - время проведения измерений
- время проведения измерений
Таблица 1 .Начальные данные.
|
N |
|
|
|
|
|
|
|
6.1 |
10 |
5 |
1 |
10 |
100 |
100 |
2.Программа для поиска коэффициентов полинома:
clear; close all;
‘ввод начальных данных’
s0=10; s1=5;
r=10; m=100; t=100;
dt=t/m; -интервал проведения измерений
R=r^2*eye(m); -задаем матрицу ковариаций шума
‘Моделируем векторы случайных коэффициентов и шума’
x0=normrnd(0,s0,1,1);
x1=normrnd(0,s1,1,1);
x=[x0,x1,0];
T=0:dt:t-dt;
v=normrnd(0,r,m,1);
H=[ones(m,1),transpose(T),transpose(T.^2)]; -формируем матрицу Н
y=H*transpose(x)+v; -формируем вектор у
p=diag([s0^2,s1^2,0.00001]); - задаем матрицу ковариаций коэффициентов
‘вычисляем квадраты диагональных элементов матриц ковариаций оценок’
p1=(transpose(H)*H)^-1*transpose(H)*r*H*(transpose(H)*H)^-1;
k1=(transpose(H)*H)^-1*transpose(H);
p2=(transpose(H)*R^-1*H)^-1;
k2=p2*transpose(H)*R^-1;
p3=(p^-1+transpose(H)*R^-1*H)^-1;
k3=p3*transpose(H)*R^-1;
‘вычисляем оценки коэффициентов и векторов измерения’
xo1=k1*y; yo1=H*xo1;
xo2=k2*y; yo2=H*xo2;
xo3=k3*y; yo3=H*xo3;
‘графики строим’
plot(T,y)
hold on;
plot(T, -2.3816-8.3298*T-0.0005*T.^2, 'red')
plot(T,y)
hold on;
plot(T, -2.1959-8.3380*T--0.0004*T.^2,'red')
3.Результаты вычислений.
Таблица 2. Значения, оценки коэффициентов и с.к.о.
|
X0hat |
X1hat |
X2hat |
S0 |
S1 |
S2 |
|
|
Ист |
-4.3256 |
-8.3279 |
0 |
10 |
5 |
0 |
|
МНК |
-2.3816 |
-8.3298 |
-0.0005 |
0,5882 |
0,0283 |
2,6833е-4 |
|
ОМНК |
-2.3816 |
-8.3298 |
-0.0005 |
0,5882 |
0,0283 |
2,6833е-4 |
|
ММНК |
-2.1959 |
-8.3380 |
-0.0004 |
0,5829 |
0,0272 |
2,663е-4 |
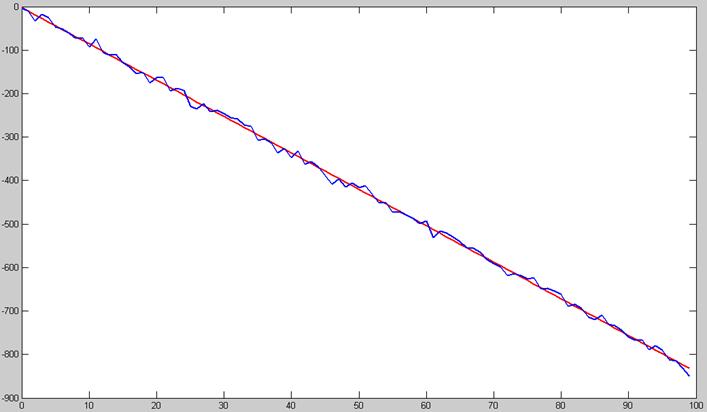
Рис.1 .График у(синий) и уоцен(красный) для МНК и ОМНК.
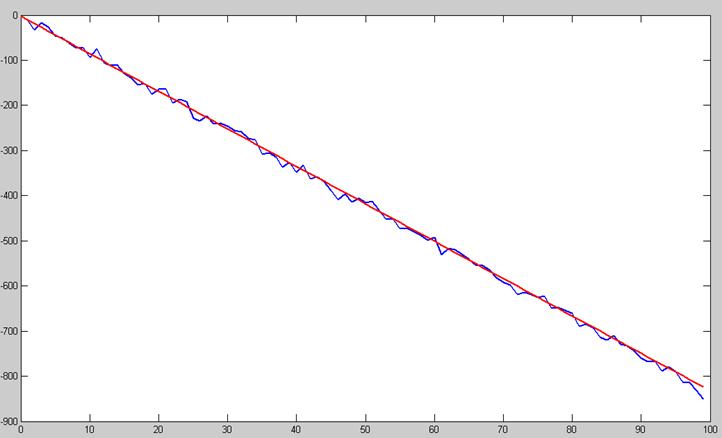
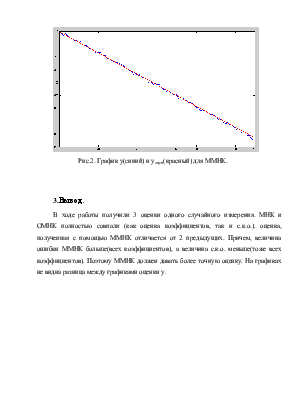
Рис.2. График у(синий) и уоцен(красный) для ММНК.
3.Вывод.
В ходе работы получили 3 оценки одного случайного измерения. МНК и ОМНК полностью совпали (как оценка коэффициентов, так и с.к.о.). оценка, полученная с помощью ММНК отличается от 2 предыдущих. Причем, величина ошибки ММНК больше(всех коэффициентов), а величина с.к.о. меньше(тоже всех коэффициентов). Поэтому ММНК должен давать более точную оценку. На графиках не видна разница между графиками оценки у.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.