Определение аэродинамических характеристик осесимметричного тела. Вариант 1

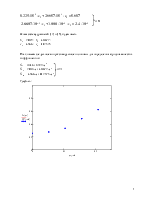
силы: X_изм, Y_1изм, Y_2изм – лежат в одной плоскости, проходящей через ось вращения. Замер аэродинамических сил в двух точках А и В позволяет найти помимо коэффициентов С_x и С_y еще и значение коэффициента момента С_mz, а также положение центра давления С.

В процессе проведения эксперимента при различных углах атаки α определяются массы грузов m_x, m_y1, m_y2, уравновешивающих через систему рычагов аэродинамические силы X_изм, Y_1изм, Y_2изм. Для каждого угла атаки трубкой Пито-Прандля находится разность давлений P₀-P, где P₀ – давление заторможенного потока, а P – статическое давление. Эта разность фиксируется водяным дифференциальным манометром в виде разницы высот  Δh_пито в сообщающихся трубках, к которым подведены соответственно давления P₀ и P.

Результаты измерений сведём в Таблицу 1:

  Таблица1

Обработка результатов измерений

1. Нахождение скоростного напора и скорости

В соответствии с интегралом Бернулли для потока с малой дозвуковой скоростью

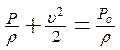
где υ – скорость набегающего на модель потока воздуха, Р – статическое давление, Р₀ – давление заторможенного потока, имеем 

Разность давлений Р₀-Р уравновешивается весом столба жидкости (воды) в коленах дифференциального манометра

, где g=9.81 [м/с²] – ускорение силы тяжести,

ρ_ж=1000 [кг/м³ ] – плотность воды,

Δh [м]=0.001Δh [мм] – разность уровней воды в коленах сообщающихся сосудов.

Отсюда 

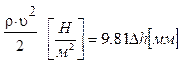(1)

Для нахождения υ используем уравнение (1) и уравнение состояния

.

Примем:

P=10⁵ [Па],

R=287.1 [Дж/кг*°К],

T=300°К.

Тогда ρ=1.161 кг/м³,

       (2)

Результаты вычислений  и υ сведем в Таблицу 2:

Таблица 2

Значение скоростного напора и скорости потока для различных углов атаки.               

2. Вычисление величин X, Y_1, Y₂ и Y

Основные соотношения: X=k_xgm_x; Y₁=k_Ygm_y1; Y₂=k_Ygm_y2; Y=Y₁+Y_{2 .}

Переходные коэффициенты для весов равны: k_x=2.35, k_y=2.5 .

Результаты вычислений сведём в Таблицу 3:

Таблица 3

Значение X_, Y_1, Y_2,Y для различных углов атаки.

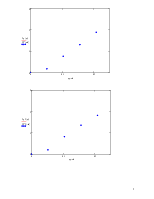
3. Вычисление коэффициентов С_x ,C_y , C_y2.

Сила лобового сопротивления Х, подъёмная сила Y и составляющая подъемной силы Y2 связаны с соответствующими безразмерными коэффициентами С_x ,C_y , C_y2 соотношениями:                                                       

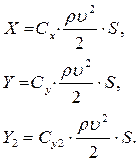
(3)

(4)

(5)

где площадь миделя S: 

Подставляя в зависимости (3), (4), (5) значения скоростного напора  (Таблица 2) и сил X_, Y_1, Y (Таблица 3), получим величины коэффициентов силы лобового сопротивления С_x ,  коэффициентов подъёмной силы C_y  и составляющей подъёмной силыC_y2.

Сведём результаты вычислений в Таблицу 4:

Таблица 4

Значение коэффициентов С_x ,C_y , C_y2  при  различных углах атаки α.

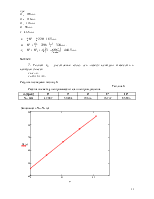
4. Построение аппроксимирующих полиномов для аэродинамических коэффициентов  С_x ,C_y, C_y2.

Аппроксимируем полученные значения аэродинамических коэффициентов полиномами, используя метод наименьших квадратов.

Учитывая, что для осесимметричного тела зависимость  должна быть чётной, запишем аппроксимирующий полином для коэффициента силы лобового сопротивления в виде:

      (6)

где угол задаём в радианах.

Тогда из условия минимизации квадрата отклонения приближенной зависимости Сх  (Формула (6)) от измеренных значений Схизм     в заданных точках, получим:

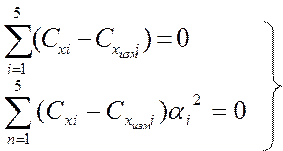(7)

Или

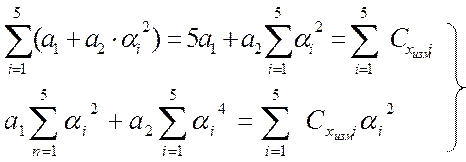(8)

где ;     ;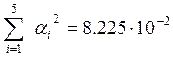

 ;         

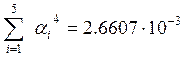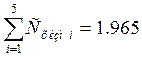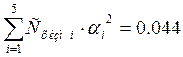
Итак, для определения коэффициентов   в формуле (6) будем иметь два уравнения:

(9)

Решая систему (9), получим:        

 ; 

Приближенная зависимость для Сх  будет иметь вид:

.

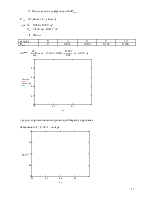
Зависимость аэродинамических коэффициентов  и , где угол атаки задаётся в радианах, будем аппроксимировать полиномами:

            (11)

           (12)

В формулы (11) и (12) угол  входит только в нечётных степенях