Структурный и кинематический анализ плоского рычажного механизма с тремя подвижными звеньями

Балтийский Государственный Технический Университет

«ВОЕНМЕХ» им. Д.Ф.Устинова

Лабораторная работа №1

Структурный и кинематический анализ плоского рычажного механизма

(установка № 3-15)

Выполнил:              Гайдай А.И.

Группа:                    М151

Преподаватель:      Лавров В.Ю.

Санкт-Петербург

2007г.

Цель работы: Изучить строение механизма, сделать его структурный анализ. Получить зависимость перемещения выходного звена от характера движения входного, используя для аппроксимации  разложение функции в ряд Фурье.

1.  Структурный анализ механизма

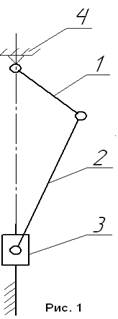В состав механизма входит три подвижных звена (рис 1): 1- кривошип

2- шатун

3- ползун

Пассивных связей нет.

Звенья образуют 4 кинематические  пары пятого класса: стойка-кривошип, кривошип-шатун, шатун-ползун, ползун-стойка.

Число степеней свободы для данного механизма по формуле Чебышева для плоских механизмов:

, гдеn – количество подвижных звеньев,

p₅, p₄ – количество кинематических пар 5-го и 4-го класса соответственно.         

Структурное деление механизма по Ассуру - Артоболевскому:

Входное звено (кривошип):                                                   Структурная группа:                                                                   

                                                                                    

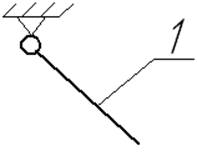
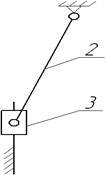
Число степеней свободы:                                Число степеней свободы:

                             

В структурной группе две кинематические пары:

ползун-стойка и ползун- шатун.

Результаты структурного анализа:     Механизм состоит из четырех звеньев: кривошипа 1, шатуна 2, ползуна 3 и стойки 4 (рис. 1). Входным звеном является кривошип, выходным - ползун. Механизм образован одной структурной группой 2-го класса 2-го порядка и является механизмом 2-го класса, 2-го порядка. Число степеней свободы равно 1.

2.  Кинематический анализ механизма.

Функция зависимости перемещения ползуна от угла поворота кривошипа S(φ) с шагом Δφ=20°:

φ	0	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360
Х	190	196	210	223	237	250	261	267	269	270	266	259	250	238	226	212	200	192	190
S	0	6	20	33	47	60	71	77	79	80	76	69	60	48	36	22	10	2	0

Перейдем от функции S(φ) к функции S(t):

Δφ=ωΔt         Δt= Δφ /ω          ω = сonst = 50 [рад/с]

Формула для расчета шага  

Функция зависимости перемещения ползуна от времени S(t):

n            t                    S(t)

0.   0.000e+000   0.000e+000                                                                                     

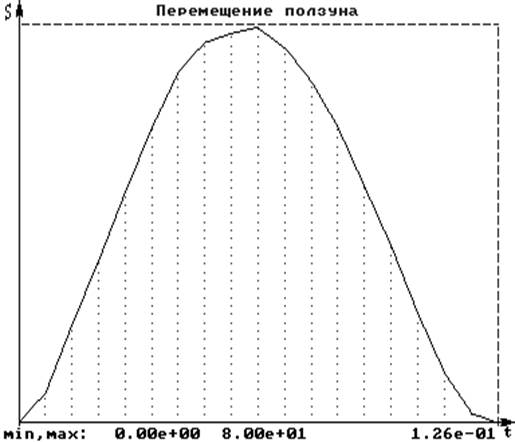  1.   7.000e-003   6.000e+000

2.   1.400e-002   2.000e+001

3.   2.100e-002   3.300e+001

4.   2.800e-002   4.700e+001

5.   3.500e-002   6.000e+001

6.   4.200e-002   7.100e+001

7.   4.900e-002   7.700e+001

8.   5.600e-002   7.900e+001

9.   6.300e-002   8.000e+001

10.   7.000e-002   7.600e+001

11.   7.700e-002   6.900e+001

12.   8.400e-002   6.000e+001

13.   9.100e-002   4.800e+001

14.   9.800e-002   3.600e+001

15.   1.050e-001   2.200e+001

16.   1.120e-001   1.000e+001

17.   1.190e-001   2.000e+000

18.   1.260e-001   0.000e+000

Разложим функцию S(t) в ряд Фурье, т.е. заменим ее тригонометрическим полиномом вида:

 , где  Т= 2π / ω =2х3.14/50=0.1256 [c] – время одного полного оборота кривошипа ;

  - амплитуда сигнала на j-й частоте

Частота сигнала для j-й гармоники  

Так как Функция S(t) задана таблицей значений в конечном числе точек m, то максимальное число членов ряда n_max= m/2 = 9.

Коэффициенты ряда Фурье для функции заданной в m точках вычисляются по следующим формулам:

 ,

где S_i – значения функции S(t),    i=0,1,2…m-1.

Функция S(t), разложенная в ряд Фурье. Количество учитываемых членов равно 9:

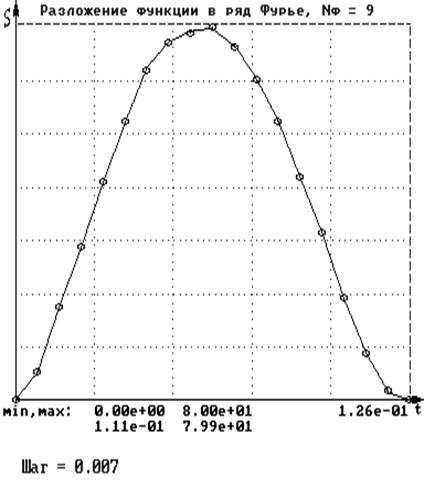                                                                                                     n               t                    S                  Ряд

0.   0.000e+000   0.000e+000   1.111e-001

1.   7.000e-003   6.000e+000   5.889e+000

2.   1.400e-002   2.000e+001   2.011e+001

3.   2.100e-002   3.300e+001   3.289e+001

4.   2.800e-002   4.700e+001   4.711e+001

5.   3.500e-002   6.000e+001   5.989e+001

6.   4.200e-002   7.100e+001   7.111e+001

7.   4.900e-002   7.700e+001   7.689e+001

8.   5.600e-002   7.900e+001   7.911e+001

9.   6.300e-002   8.000e+001   7.989e+001

10.   7.000e-002   7.600e+001   7.611e+001

11.   7.700e-002   6.900e+001   6.889e+001

12.   8.400e-002   6.000e+001   6.011e+001

13.   9.100e-002   4.800e+001   4.789e+001