Структурный и кинематический анализ плоского рычажного механизма с тремя подвижными звеньями, страница 2

14.   9.800e-002   3.600e+001   3.611e+001

15.   1.050e-001   2.200e+001   2.189e+001

16.   1.120e-001   1.000e+001   1.011e+001

17.   1.190e-001   2.000e+000   1.889e+000

18.   1.260e-001   0.000e+000   1.111e-001 

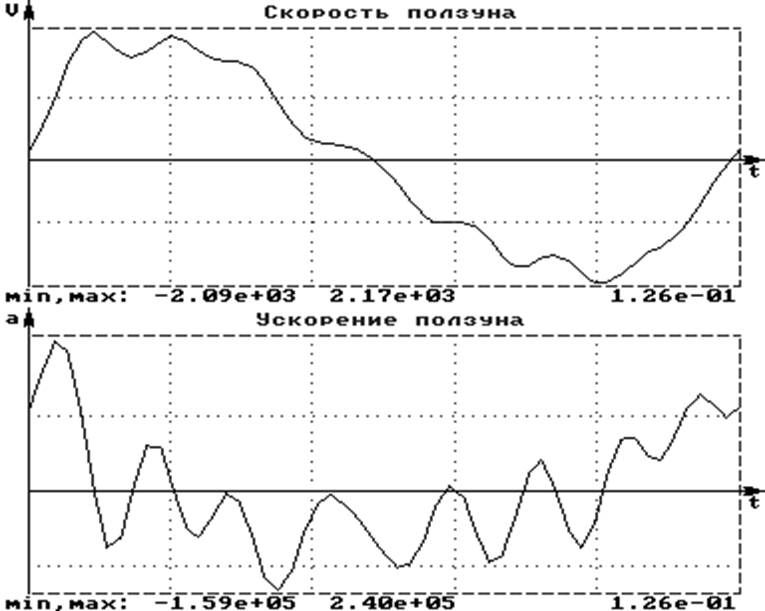
После дифференцирования получаем функции скорости ползуна V(t) и  ускорения A(t):

  

n          S(t)                Ряд               1-я пр-я          2-я пр-я

0   0.000e+000   1.111e-001     1.809e+002   1.304e+005

1   6.000e+000   5.889e+000    1.612e+003   2.251e+005

2   2.000e+001   2.011e+001    2.042e+003   -8.955e+004

3   3.300e+001   3.289e+001    1.836e+003   7.137e+004

4   4.700e+001   4.711e+001    2.046e+003   -5.900e+004

5   6.000e+001   5.989e+001    1.694e+003   -4.062e+003

6   7.100e+001   7.111e+001    1.335e+003   -1.377e+005

7   7.700e+001   7.689e+001    4.149e+002   -6.525e+004

8   7.900e+001   7.911e+001    2.688e+002   -2.055e+004

9   8.000e+001   7.989e+001   -1.396e+002   -9.946e+004

10   7.600e+001   7.611e+001   -9.220e+002   -8.015e+004

11   6.900e+001   6.889e+001   -1.042e+003   -7.742e+003

12   6.000e+001   6.011e+001   -1.602e+003   -1.046e+005

13   4.800e+001   4.789e+001   -1.681e+003   4.901e+004

14   3.600e+001   3.611e+001   -1.879e+003   -9.132e+004

15   2.200e+001   2.189e+001   -1.955e+003   8.031e+004

16   1.000e+001   1.011e+001   -1.469e+003   4.963e+004

17   2.000e+000   1.889e+000   -7.378e+002   1.535e+005

18   0.000e+000   1.111e-001    1.809e+002    1.304e+005

Для уточнения количества учитываемых членов ряда Фурье анализируем спектр:

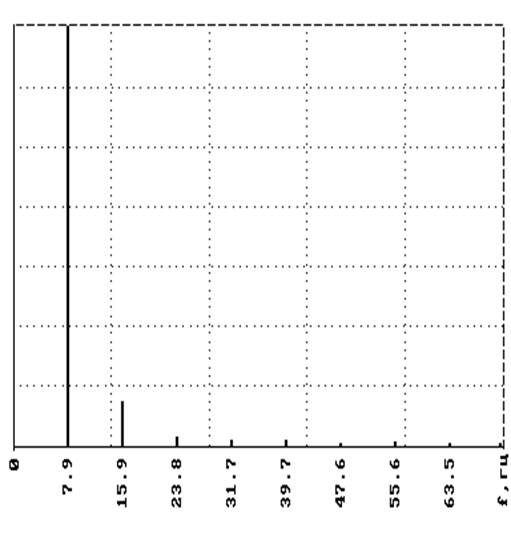                                    амплитудный спектр

i   Частота [Гц]    Амплитуда          

0   0.000e+000     8.844e+001               

1   7.937e+000    -3.882e+001  

2   1.587e+001   -4.117e+000  

3   2.381e+001   -7.778e-001  

4   3.175e+001   -4.185e-001  

5   3.968e+001   -2.912e-001 

6   4.762e+001    1.111e-001 

7   5.556e+001    -2.269e-001 

8   6.349e+001    2.023e-001  

9   7.143e+001    2.222e-001 

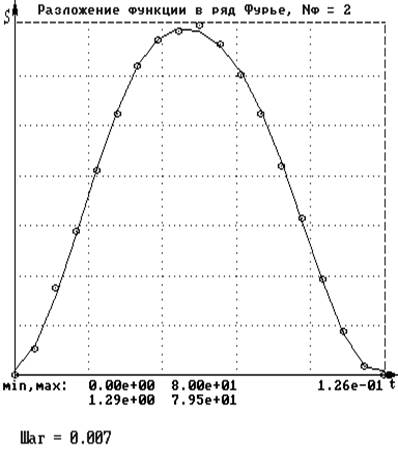
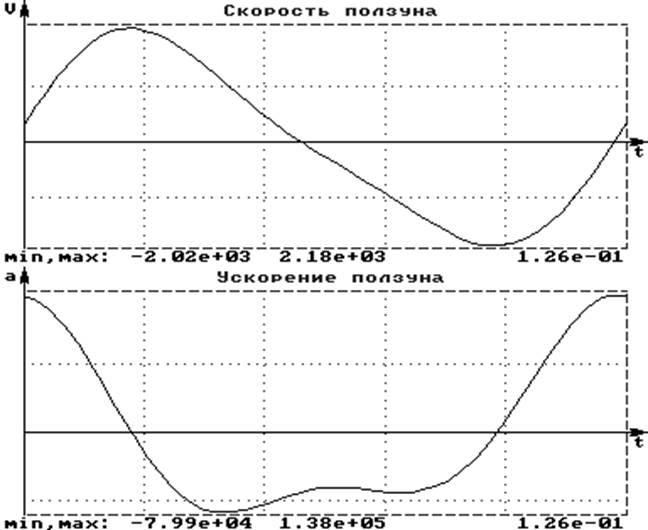
Для получения удовлетворительных результатов дифференцирования необходимо учитывать только два члена ряда Фурье.  Результаты аппроксимации и дифференцирования функции с учетом двух первых членов:

                                                                                  n             t                       S(t)                   Ряд

  0.   0.000e+000   0.000e+000   1.290e+000

  1.   7.000e-003   6.000e+000   6.872e+000

  2.   1.400e-002   2.000e+001   1.800e+001

  3.   2.100e-002   3.300e+001   3.245e+001

  4.   2.800e-002   4.700e+001   4.753e+001

  5.   3.500e-002   6.000e+001   6.084e+001

  6.   4.200e-002   7.100e+001   7.083e+001

  7.   4.900e-002   7.700e+001   7.697e+001

  8.   5.600e-002   7.900e+001   7.950e+001

  9.   6.300e-002   8.000e+001   7.892e+001

 10.   7.000e-002   7.600e+001   7.559e+001

 11.   7.700e-002   6.900e+001   6.951e+001

 12.   8.400e-002   6.000e+001   6.055e+001

 13.   9.100e-002   4.800e+001   4.883e+001

 14.   9.800e-002   3.600e+001   3.517e+001

 15.   1.050e-001   2.200e+001   2.130e+001

 16.   1.120e-001   1.000e+001   9.549e+000

 17.   1.190e-001   2.000e+000   2.316e+000

 18.   1.260e-001   0.000e+000   1.290e+000

n         S(t)                  Ряд                  1-я пр-я          2-я пр-я

0   0.000e+000   1.290e+000   3.336e+002   1.375e+005

1   6.000e+000   6.872e+000   1.235e+003   1.152e+005

2   2.000e+001   1.800e+001   1.889e+003   6.869e+004

3   3.300e+001   3.245e+001   2.174e+003   1.229e+004

4   4.700e+001   4.753e+001   2.077e+003  -3.773e+004

5   6.000e+001   6.084e+001   1.689e+003  -6.953e+004

6   7.100e+001   7.083e+001   1.154e+003  -7.988e+004

7   7.700e+001   7.697e+001   6.079e+002  -7.424e+004

8   7.900e+001   7.950e+001   1.275e+002  -6.298e+004

9   8.000e+001   7.892e+001  -2.833e+002  -5.557e+004

10   7.600e+001   7.559e+001  -6.686e+002  -5.568e+004

11   6.900e+001   6.951e+001  -1.072e+003  -5.941e+004

12   6.000e+001   6.055e+001  -1.487e+003  -5.759e+004

13   4.800e+001   4.883e+001  -1.843e+003  -4.095e+004

14   3.600e+001   3.517e+001  -2.017e+003  -5.716e+003

15   2.200e+001   2.130e+001  -1.890e+003   4.328e+004

16   1.000e+001   9.549e+000  -1.408e+003   9.341e+004

17   2.000e+000   2.316e+000  -6.168e+002   1.289e+005

18   0.000e+000   1.290e+000   3.336e+002   1.375e+005

Выводы: При первой аппроксимации функции S(t) с последующим двойным дифференцированием были получены сильно искаженные функции скорости и ускорения. Это произошло из-за большой чувствительности данной операции к скачкообразным изменениям функции, которые были вызваны неточностью измерений. Анализ спектра позволил установить, что существенным, кроме А₀/2, является только два первых слагаемых. При числе учитываемых членов ряда равном 2 удается добиться удовлетворительно аппроксимации. Наиболее точно значения скоростей и ускорений найдены для фаз удаления и возврата, а в фазах выстоя функции определены с большей погрешностью.