Общая характеристика методов повышения помехоустойчивости систем передачи командно-программной информации, страница 7

d₀=1+m₀

Для обеспечения возможности исправления'всех ошибок кратности до m_и включительно необходимо, чтобы принятая кодовая комбинация осталась в подмножестве, лежащем в окрестности переданной разрешенной кодовой комбинации. D_i>1+2m_и

Код, который может исправлять ошибки кратности m_и, может обнаружить ошибки кратности 2m_и

Кодовое расстояние, определяющее корректирующую способность кода, зависит от избыточности последнего, т.е. от количества проверочных разрядов г = п – k.

Таблица 12..3

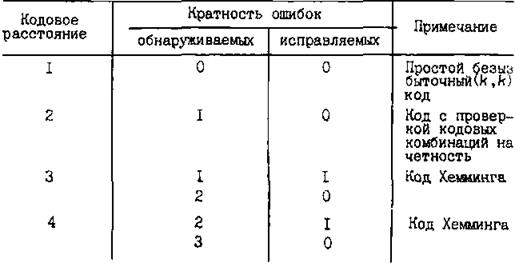
Коды с d = 3 и 4, которые позволяют обнаруживать и исправлять одиночные ошибки или обнаруживать двойные и исправлять одиночные ошибки, в литературе обычно называют кодами Хемминга

Рассмотрим классификацию помехоустойчивых кодов. Известно большое число кодов, позволяющих успешно бороться с различными видами  .помех. Все эти коды обладают избыточностью, величина которой в той или иной степени определяет их корректирующие возможности. Разнообразие помехоустойчивых кодов отображается на рис.12.7, где показана их классификация. Блочными кодами называются коды, в которых каждому сообщению ставится в однозначное соответствие блок из п  символов или блоки с разным числом символов. В соответствии с этим блочные коды делятся на равномерные и неравномерные.

Рис. 12.7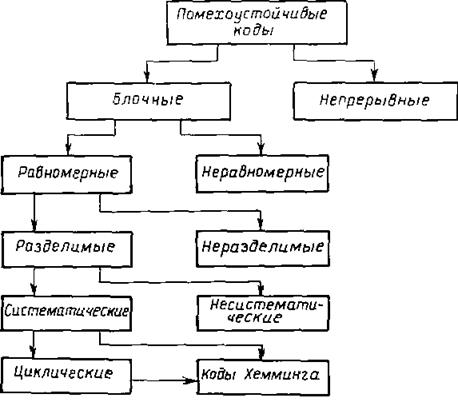

В практике передачи информации наибольшее распространение получили равномерные коды с постоянным числом символов n  , что обеспечивает более надежную пословную синхронизацию передающей и приемной аппаратуры канала связи.

Непрерывными кодами называются такие коды, у которых операции кодирования и декодирования совершаются непрерывно. Эти коды представляют собой непрерывную последовательность информационных и проверочных символов. К непрерывным кодам относятся рекуррентные коды, у которых значения проверочных символов и их место в кодовой комбинации определяются по рекуррентной формуле

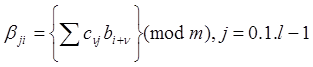
Значение правой части определяется по mod m  .что означает, что после проведения обычных вычислительных операций удерживается лишь остаток от деления полученной величины на основание кода m (например, 7 по  mod 4 дает 3). Суммирование необходимо для сохранения алфавита (разрядности).

Код Хеминга Блочный равномерный групповой код, позволяет корректировать однократн. Ошибки. В основе лежит проверка на четность

Код формируется так. а₁ а2a3 а4 a5 a6 a7

n=5 к=2 а1=a2+a1  а2=a2  а3=a1

Декодирование а1+a2+a1=0(1)  а2+a2=0(1),     а3+a1=0(1)

Равномерные блочные  кодыбывают разделимыми и неразделимые.

Разделимые коды символы разделены на информационные и проверочные.

Циклические коды в основе многочлены переменной х. Коэффициенты многочленов – сообщение. Обнаружение ошибок –используются коды многочлены котрорых делятся без остатка на заранее выбранный многочлен.

Сверочные коды. При использовании блочных (n,к) кодов для формир кодовых символов последовательность поступающих инф. Символов разбивается на блоки  по к инф. Симв. Которые в рез. Кодирования преобразуются в  символов, причем кодовые слова формируются независимо. Кодовые символы вычисляются по текущему блоку последних информационных символов для каждого такта работы кодир устр-ва. Поэтому эти коды наз. цепными.

Таким образом, удается резко увеличить помехозащищенность каналов связи.