






ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ
![]()
Кафедра “Прикладная математика”
Домашнее задание № 1
“Метод непосредственного развертывания”
Выполнила:
студентка группы ЭТ-401
Кожевникова Е. М.
Проверил:
доц. Вашакидзе Л. С.
Санкт-Петербург
2006
Для матрицы ![]() методом непосредственного развертывания
найти все собственные числа и собственные векторы. Записать ее спектральное
разложение.
методом непосредственного развертывания
найти все собственные числа и собственные векторы. Записать ее спектральное
разложение.
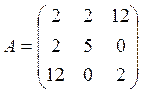 .
.
Если для некоторого
ненулевого вектора ![]() выполняется равенство
выполняется равенство
|
|
(1) |
то ![]() и
и ![]() называются соответственно
собственным значением и собственным вектором матрицы
называются соответственно
собственным значением и собственным вектором матрицы ![]() .
Если выражение (1) записать в виде
.
Если выражение (1) записать в виде
|
|
(2) |
то эта однородная система (правая часть равна нулю) линейных алгебраических уравнений имеет ненулевое решение только тогда, когда ее определитель равен нулю.
Следовательно,
|
|
(3) |
Это выражение
называется характеристическим уравнением (вековым уравнением) матрицы ![]() .
.
Составим
характеристическое уравнение для заданной матрицы ![]() :
:
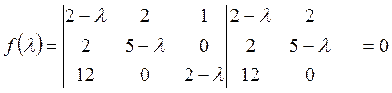 .
.
Развернем этот определитель, дополнив его двумя первыми столбцами:
![]()
![]() .
.
В развернутом виде
получаем характеристическое уравнение, которое является алгебраическим
многочленом (полиномом) третьей степени относительно неизвестного ![]() .
.
![]()
или
![]() .
.
Корнями этого
уравнения являются собственные значения матрицы ![]() .
Так как матрица
.
Так как матрица ![]() симметричная, то
собственными значениями являются действительные числа.
симметричная, то
собственными значениями являются действительные числа.
Задача нахождения собственных значений сводится к решению нелинейного уравнения третьего порядка.
Решение нелинейного уравнения
С помощью программы
MATLAB строим график функции ![]() , заменяя аргумент
, заменяя аргумент
![]() на
на ![]() ,
а значение функции
,
а значение функции ![]() на
на ![]() .
Определяем интервалы точек пересечения графика функции с осью
.
Определяем интервалы точек пересечения графика функции с осью ![]() .
.
Программа для построения графика функции:
x=-20:1:20;
y=((x-9).*x-124).*x+708;
plot(x,y,'r','linewidth',3);grid
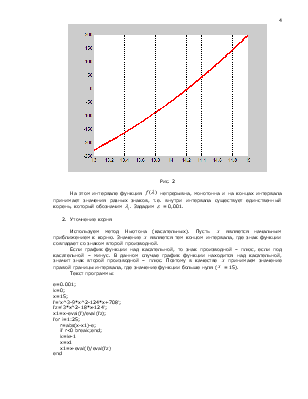
График функции изображен на рис. 1.
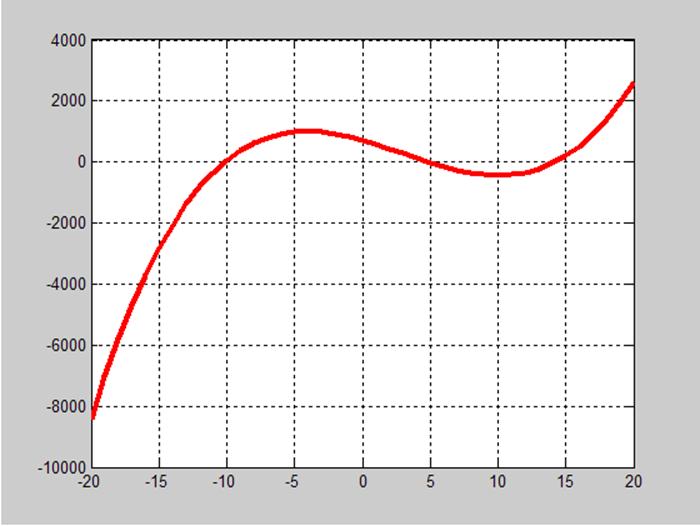
Рис. 1
Замечание. Достаточно
получить одну точку пересечения графика с осью ![]() и
уточнить один корень.
и
уточнить один корень.
График пересекает
ось ![]() между значениями 13 и 15. Еще раз
выполним эту программу на интервале от 13 до 15 с шагом 0,1.
между значениями 13 и 15. Еще раз
выполним эту программу на интервале от 13 до 15 с шагом 0,1.
x=13:0.1:15;
y=((x-9).*x-124).*x+708;
plot(x,y,'r','linewidth',3);grid
График функции изображен на рис. 2
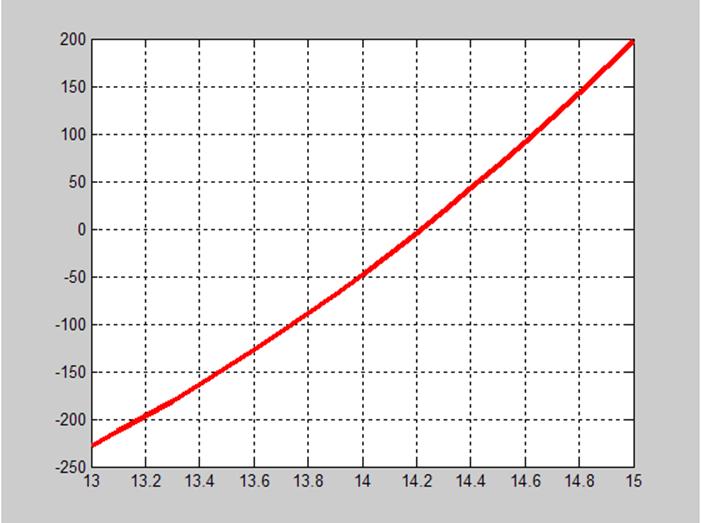
Рис. 2
На этом интервале
функция ![]() непрерывна, монотонна и на концах
интервала принимает значения разных знаков, т.е. внутри интервала существует
единственный корень, который обозначим
непрерывна, монотонна и на концах
интервала принимает значения разных знаков, т.е. внутри интервала существует
единственный корень, который обозначим ![]() .
Зададим
.
Зададим ![]() = 0,001.
= 0,001.
Используем метод
Ньютона (касательных). Пусть ![]() является
начальным приближением к корню. Значение
является
начальным приближением к корню. Значение ![]() является
тем концом интервала, где знак функции совпадает со знаком второй производной.
является
тем концом интервала, где знак функции совпадает со знаком второй производной.
Если график функции
над касательной, то знак производной – плюс, если под касательной – минус. В
данном случае график функции находится над касательной, значит знак второй
производной – плюс. Поэтому в качестве ![]() принимаем
значение правой границы интервала, где значение функции больше нуля (
принимаем
значение правой границы интервала, где значение функции больше нуля (![]() = 15).
= 15).
Текст программы:
e=0.001;
k=0;
x=15;
f='x^3-9*x^2-124*x+708';
fz='3*x^2-18*x-124';
x1=x-eval(f)/eval(fz);
for i=1:25;
r=abs(x-x1)-e;
if r<0 break;end;
k=k+1
x=x1
x1=x-eval(f)/eval(fz)
end
k =1 x = 14.2954 x1 = 14.2198
k =2 x = 14.2198 x1 = 14.2189
Тогда
![]() = 14,2189.
= 14,2189.
Разделим уголком ![]() на
на ![]() :
:
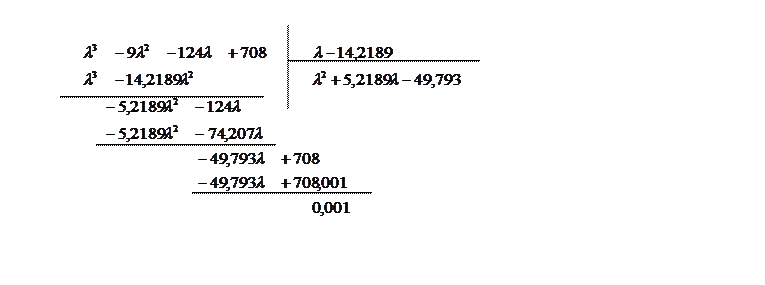
Решим полученное квадратное уравнение:
![]() ;
;
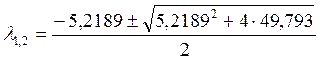 ;
;
![]() ;
;
![]() .
.
Для каждого
собственного значения ![]() находим соответствующие им
собственные векторы:
находим соответствующие им
собственные векторы:
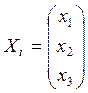 .
.
Для
![]() = 14,2189 однородная система имеет
вид:
= 14,2189 однородная система имеет
вид:
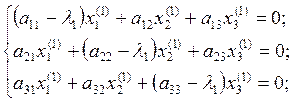
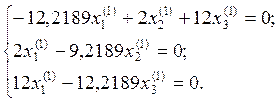
Эта система имеет
бесчисленное множество решений. Так как минор ![]() 0,
то переменные
0,
то переменные ![]() и
и ![]() – базисные,
– базисные, ![]() – свободная.
– свободная.
Рассмотрим первые
два уравнения, в каждом из которых перенесем в правую часть третье слагаемое,
заменив ![]() и решим систему второго порядка
относительно
и решим систему второго порядка
относительно ![]() и
и ![]() .
.
Пусть ![]() = 1
= 1
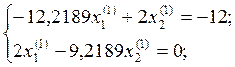
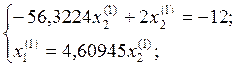
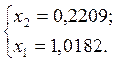
Тогда
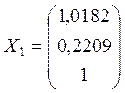 .
.
Находим длину этого вектора (т.е. его норму) и делим каждую координату на длину этого вектора:
![]() ;
;
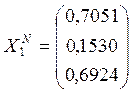 .
.
Для
![]() = 4,914 однородная система имеет
вид:
= 4,914 однородная система имеет
вид:
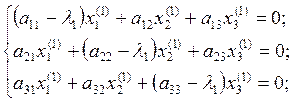
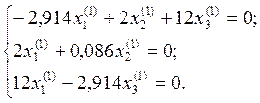
Пусть ![]() = 1
= 1
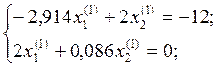
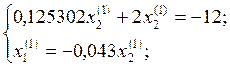
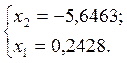
Тогда
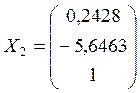 .
.
Находим длину этого вектора (т.е. его норму) и делим каждую координату на длину этого вектора:
![]() ;
;
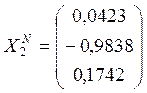 .
.
Для ![]() = -10,1329
однородная система имеет вид:
= -10,1329
однородная система имеет вид:
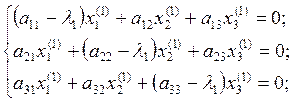
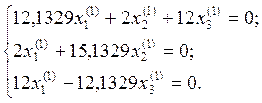
Пусть ![]() = 1
= 1
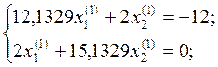
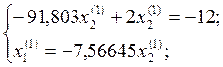
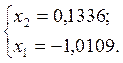
Тогда
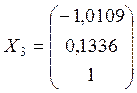 .
.
Находим длину этого вектора (т.е. его норму) и делим каждую координату на длину этого вектора:
![]() ;
;
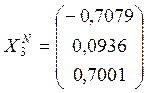 .
.
Спектральное разложение матрицы ![]()
Введем матрицу ![]() , столбцы которой являются
собственными ортонормированными векторами матрицы
, столбцы которой являются
собственными ортонормированными векторами матрицы ![]() :
:
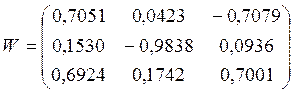
Введем диагональную
матрицу ![]() с собственными значениями матрицы
с собственными значениями матрицы ![]() на диагонали:
на диагонали:
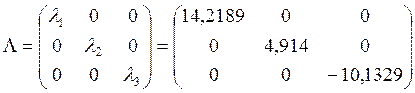 .
.
Можно записать спектральное
разложение матрицы ![]() по базису ее собственных векторов и
чисел в MATLAB:
по базису ее собственных векторов и
чисел в MATLAB:
L=[14.2189 0 0; 0 4.914 0; 0 0 -10.1329]
W=[0.7051 0.0423 -0.7079; 0.1530 -0.9838 0.0936; 0.6924 0.1742 0.7001]
A=W*L*W'
L =
14.2189 0 0
0 4.9140 0
0 0 -10.1329
W =
0.7051 0.0423 -0.7079
0.1530 -0.9838 0.0936
0.6924 0.1742 0.7001
A =
2.0001 2.0008 11.9999
2.0008 5.0002 0.0002
11.9999 0.0002 1.9994
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.