


























































1 ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЙ
Пусть функция ![]() определена
или на всей числовой оси, или для всех
определена
или на всей числовой оси, или для всех ![]() больших
некоторого числа.
больших
некоторого числа.
Определение 1.1. Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() если
каково бы ни было положительное число
если
каково бы ни было положительное число ![]() можно
найти такое число
можно
найти такое число ![]() что для всех
что для всех ![]() больших
больших ![]() выполняется
неравенство
выполняется
неравенство
![]()
Символическая запись этого определения –
![]()
Записывается это следующим
образом: ![]()
Определение
1.2. Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() если
каково бы ни было положительное число
если
каково бы ни было положительное число ![]() можно
найти такое число
можно
найти такое число ![]() что для всех
что для всех ![]() меньших
меньших ![]() выполняется
неравенство
выполняется
неравенство ![]()
Символическая запись этого определения –
![]()
Определение
1.3. Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() слева,
если каково бы ни было положительное число
слева,
если каково бы ни было положительное число ![]() найдется
такое число
найдется
такое число ![]() (меньшее
(меньшее ![]() ), что
для всех
), что
для всех ![]() лежащих между
лежащих между![]() и
и ![]()
![]() выполняется
неравенство
выполняется
неравенство ![]()
Символическая запись этого определения –
![]()
Символ ![]() означает, что
означает, что ![]() стремится к
стремится к ![]() слева,
т. е. оставаясь меньше
слева,
т. е. оставаясь меньше ![]()
Определение
1.4. Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() справа,
если каково бы ни было положительное число
справа,
если каково бы ни было положительное число ![]() найдется
такое число
найдется
такое число ![]() (большее
(большее ![]() ), что
для всех
), что
для всех ![]() лежащих между
лежащих между ![]() и
и ![]()
![]() выполняется неравенство
выполняется неравенство
![]()
Символическая запись этого определения –
![]()
Пределы функции при ![]() и при
и при ![]() называются
односторонними пределами. Если оба односторонних предела существуют и равны
между собой, то говорят, что функция
называются
односторонними пределами. Если оба односторонних предела существуют и равны
между собой, то говорят, что функция ![]() имеет двусторонний
предел при
имеет двусторонний
предел при ![]() или просто имеет предел при
или просто имеет предел при ![]()
Определение 1.5. Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() , если
каково бы ни было
, если
каково бы ни было ![]() можно найти такие числа
можно найти такие числа ![]() и
и ![]() (
(![]() ), что для всех
), что для всех ![]() лежащих
в интервале
лежащих
в интервале ![]() (за исключением, быть может, точки
(за исключением, быть может, точки ![]() ), выполняется неравенство
), выполняется неравенство ![]()
Символическая запись этого определения –
![]()
![]()
![]()
Пример 1.1. Доказать,
что ![]()
Решение. Воспользуемся
определением 1.1. В данном случае ![]() Возьмем произвольное
Возьмем произвольное ![]() и рассмотрим модуль разности
и рассмотрим модуль разности
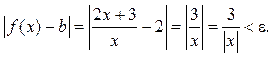
Так как ![]() то
то ![]() можно
считать положительным, т. е.
можно
считать положительным, т. е. ![]() Итак,
Итак, ![]() т. е. число
т. е. число ![]() Следовательно,
Следовательно,
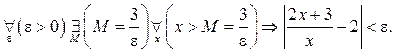
Это означает, что ![]()
Пример 1.2. Доказать,
что ![]()
Решение. Воспользуемся
определением 1.2. В данном случае ![]() Возьмем произвольное
Возьмем произвольное ![]() и рассмотрим модуль разности
и рассмотрим модуль разности
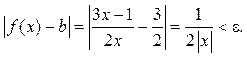
Так как ![]() то можно считать
то можно считать ![]() отрицательным,
т. е.
отрицательным,
т. е. ![]() Итак,
Итак, ![]() т. е.
число
т. е.
число ![]() Мы получили, что
Мы получили, что ![]()
Пример 1.3.
Доказать, что ![]()
Решение.
Воспользуемся определением 1.5. Возьмем произвольное ![]() Рассмотрим
модуль разности
Рассмотрим
модуль разности
![]()
![]()
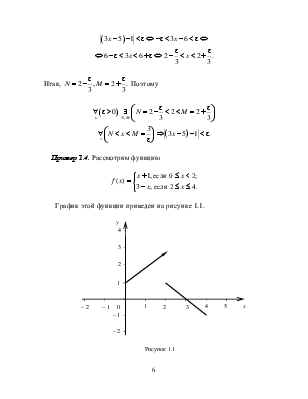
Итак, ![]() Поэтому
Поэтому
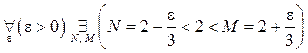
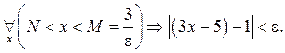
Пример 1.4. Рассмотрим функцию
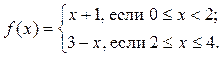
График этой функции приведен на рисунке 1.1.
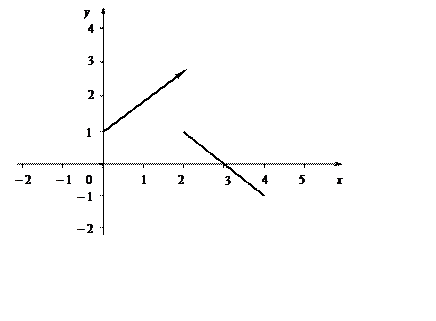
Рисунок 1.1
Найдем предел этой
функции при ![]() Рассмотрим односторонние пределы
Рассмотрим односторонние пределы
![]()
Предел слева и предел
справа не равны друг другу, поэтому функция ![]() при
при ![]() предела не имеет.
предела не имеет.
Пример 1.5.
Функции ![]() и
и ![]() при
при ![]() и
и ![]() не
имеют предела. Значения этих функций все время колеблются между
не
имеют предела. Значения этих функций все время колеблются между ![]() и
и ![]()
Упражнения. Доказать, что указанные функции имеют предел:
1.1 ![]() 1.2
1.2 ![]() 1.3
1.3 ![]()
1.4 ![]() 1.5
1.5 ![]() 1.6
1.6 ![]()
Функция ![]() называется бесконечно малой при
называется бесконечно малой при ![]() если ее предел при
если ее предел при ![]() равен
нулю. Аналогично определяются бесконечно малые функции при
равен
нулю. Аналогично определяются бесконечно малые функции при ![]() Для определенности все последующие
определения и утверждения будем формулировать только для
Для определенности все последующие
определения и утверждения будем формулировать только для ![]() но они будут справедливы для всех пяти
случаев стремления
но они будут справедливы для всех пяти
случаев стремления ![]()
Так как для бесконечно
малой функции (б. м. ф.) предел ![]() а
а ![]() то можно дать следующее определение.
то можно дать следующее определение.
Определение 2.1. Функция ![]() называется
б. м. ф. при
называется
б. м. ф. при ![]() если
каково бы ни было
если
каково бы ни было ![]() можно найти такое число
можно найти такое число ![]() что при всех
что при всех ![]() выполняется
неравенство
выполняется
неравенство ![]()
Символическая запись
![]()
Пример 2.1. Покажем, что функция ![]() является б. м. ф. при
является б. м. ф. при ![]()
Решение. Для этого надо показать, что при ![]() для любого
для любого
![]() можно найти такое
можно найти такое ![]() что
при всех
что
при всех ![]() выполняется неравенство
выполняется неравенство ![]() Имеем
Имеем 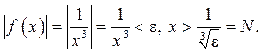 Итак,
Итак,
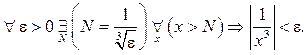
Эта же функция ![]() будет
б. м. ф. и при
будет
б. м. ф. и при ![]()
Вообще, можно показать, что
функция ![]() есть б. м. ф. при
есть б. м. ф. при ![]()
Пример 2.2. Покажем, что функция ![]() является б. м. ф. при
является б. м. ф. при ![]()
Решение. Зададим ![]() Неравенство
Неравенство ![]() очевидно, выполняется для всех тех
значений
очевидно, выполняется для всех тех
значений ![]() для которых
для которых ![]() Таким
образом, неравенство
Таким
образом, неравенство ![]() выполняется для всех
выполняется для всех ![]() расположенных между
расположенных между ![]() и
и ![]() Это значит,
что
Это значит,
что ![]() т. е. функция
т. е. функция ![]() является
б. м. ф. при
является
б. м. ф. при ![]()
Вообще, можно показать,
что функция ![]() является б. м. ф. при
является б. м. ф. при ![]()
Пример 2.3. Функция ![]() не
является б. м. ф. при
не
является б. м. ф. при ![]() так как
так как 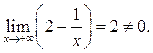
Для б. м. ф. имеют место следующие свойства.
2.1 Алгебраическая сумма конечного числа б. м. ф. есть б. м. ф.
2.2 Произведение б. м. ф. на функцию ограниченную есть б. м. ф.
2.3 Произведение конечного числа б. м. ф. есть б. м. ф.
2.4 Произведение числа на б. м. ф. есть б. м. ф.
Пример 2.4. Функция 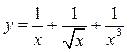 является б. м. ф. при
является б. м. ф. при ![]() так как каждое слагаемое есть б. м. ф. при
так как каждое слагаемое есть б. м. ф. при
![]() (см. пример 2.1).
(см. пример 2.1).
Пример 2.5.
Функция ![]() есть б. м. ф. при
есть б. м. ф. при ![]() так
как все функции являются б. м. ф. при
так
как все функции являются б. м. ф. при ![]() (см.
пример 2.2).
(см.
пример 2.2).
Пример 2.6. Функция ![]() является б. м. ф. при
является б. м. ф. при ![]() так как она является произведением
ограниченной функции
так как она является произведением
ограниченной функции ![]() на б.
м. ф.
на б.
м. ф. ![]() при
при ![]()
Пример 2.7.
Функция ![]() является б. м. ф. при
является б. м. ф. при ![]() так как она является произведением
ограниченной функции
так как она является произведением
ограниченной функции ![]() на б. м. ф.
на б. м. ф. ![]() при
при ![]()
Определение 2.2. Функция ![]() называется бесконечно большой
функцией (б. б. ф.) при
называется бесконечно большой
функцией (б. б. ф.) при ![]() если для любого положительного
числа
если для любого положительного
числа ![]() можно подобрать такое число
можно подобрать такое число ![]() что для всех значений
что для всех значений ![]() выполняется неравенство
выполняется неравенство ![]()
О бесконечно большой
функции (при ![]() ) говорят, что она стремится к
бесконечности, или, что она имеет бесконечный предел. Если
) говорят, что она стремится к
бесконечности, или, что она имеет бесконечный предел. Если ![]() б. б. ф. при
б. б. ф. при ![]() то это
символически записывают так:
то это
символически записывают так: ![]() Это равенство не следует
понимать в том смысле, что функция имеет предел, оно означает только, что функция
(не имея предела) является бесконечно большой.
Это равенство не следует
понимать в том смысле, что функция имеет предел, оно означает только, что функция
(не имея предела) является бесконечно большой.
Если б. б. ф. ![]() положительна
для всех достаточно больших значений
положительна
для всех достаточно больших значений ![]() то
то ![]() Если же б. б. ф.
Если же б. б. ф. ![]() отрицательна
для всех достаточно больших значений
отрицательна
для всех достаточно больших значений ![]() то
то ![]() Так, например,
Так, например, ![]()
Аналогично даются определения при ![]()
![]()
![]()
![]()
Можно доказать, что любой многочлен есть б. б. ф. при ![]()
Связь между б. м. ф. и б. б. ф. устанавливают следующие свойства.
2.5
Если ![]() является
б. б. ф., то
является
б. б. ф., то ![]() является б. м. ф.
является б. м. ф.
2.6
Если ![]() является
б. м. ф. (не обращающейся в ноль), то
является
б. м. ф. (не обращающейся в ноль), то ![]() – б.
б. ф.
– б.
б. ф.
То обстоятельство, что функция, обратная б. м.
является б. б; и наоборот, делает естественной следующую символическую запись,
часто употребляющуюся для сокращения записей: для любого ![]() верны равенства:
верны равенства:
![]()
![]()
Пример 2.8. Функция ![]() является б. б. ф. при
является б. б. ф. при ![]() тогда
тогда ![]() является
б. м. ф. при
является
б. м. ф. при ![]()
Пример 2.9. Функция ![]() является
б. м. ф. при
является
б. м. ф. при ![]() тогда
тогда ![]() является
б. б. ф. при
является
б. б. ф. при ![]()
Отметим еще следующие свойства.
2.7 Если функция ![]() имеет
предел при
имеет
предел при ![]() равный
равный ![]() то
то ![]() где
где ![]() – б. м.
ф. при
– б. м.
ф. при ![]()
2.8 Если функцию ![]() можно
представить
можно
представить ![]() где
где ![]() – б. м.
ф. при
– б. м.
ф. при ![]() то
то ![]()
Пример 2.10. Доказать, что 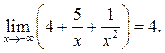
Решение. Так как функции ![]() и
и ![]() – б.
м. ф. при
– б.
м. ф. при ![]() то и их сумма является б. м. ф. Функция
то и их сумма является б. м. ф. Функция 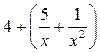 есть сумма числа 4 и б. м. ф. Значит, согласно свойства
2.8,
есть сумма числа 4 и б. м. ф. Значит, согласно свойства
2.8, 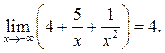
При вычислении пределов функций необходимо знать следующие теоремы.
Т1. Предел постоянной равен
самой постоянной, т. е. ![]()
Т2. Постоянный множитель
можно выносить за знак предела, т. е. ![]()
Т3. Если ![]() и
и ![]() существуют,
то
существуют,
то
![]()
Т4. ![]()
Т5. 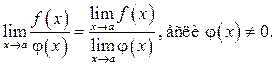
Т6. ![]()
Кроме того, мы будем пользоваться тем, что для всех
основных элементарных функций в любой точке их области определения имеет место
равенство ![]()
Если же аргумент стремится к бесконечности или к числу, которое не принадлежит области определения функции, то в каждом таком случае нахождение предела функции требует специального исследования.
Будем использовать следующие часто встречающиеся пределы:
П1. 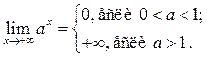
П2. 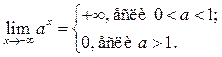
П3. 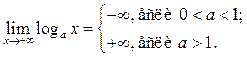
П4. 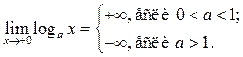
П5. 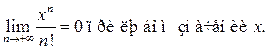
П6. ![]()
П7. ![]()
П8. ![]()
П9. ![]()
Пример 3.1.
Найти
![]()
Решение.
![]()
Пример 3.2. Найти 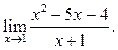
Решение.
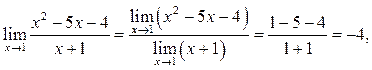
так как ![]()
Пример 3.3. Найти ![]()
Решение. Так как ![]() и
и ![]() то по Т6:
то по Т6: ![]()
Пример 3.4. Найти ![]()
Решение. 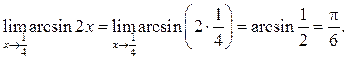
Пример 3.5.Найти 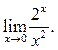
Решение. 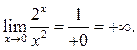
Пример 3.6. Найти 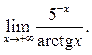
Решение.
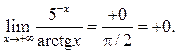
Пример 3.7. Найти 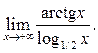
Решение. 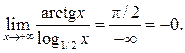
Непосредственное
применение теорем о пределах функций не всегда приводит к цели. Например, если 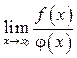 таков, что при
таков, что при ![]() и
и ![]() то говорят, что имеет место неопределенность
то говорят, что имеет место неопределенность
![]() Понимать ее следует так: отношение двух
бесконечно малых функций может быть величиной конечной, бесконечно малой,
бесконечно большой или вообще не существовать. Нахождение предела такой дроби
или установление его отсутствия называется раскрытием этой неопределенности.
Всего существует семь типов неопределенных выражений:
Понимать ее следует так: отношение двух
бесконечно малых функций может быть величиной конечной, бесконечно малой,
бесконечно большой или вообще не существовать. Нахождение предела такой дроби
или установление его отсутствия называется раскрытием этой неопределенности.
Всего существует семь типов неопределенных выражений:
![]()
Рассмотрим раскрытие отдельных видов неопределенностей.
Пусть 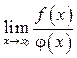 неопределенность
неопределенность ![]() т. е.
т. е. ![]() Следовательно,
Следовательно,
![]() является корнем числителя
является корнем числителя ![]() и знаменателя
и знаменателя ![]() т. е.
обе функции можно разложить на множители, одним из которых обязательно будет
т. е.
обе функции можно разложить на множители, одним из которых обязательно будет ![]() После этого можно дробь сократить на
После этого можно дробь сократить на ![]() Здесь нет сокращения на нуль, что никогда
не допустимо. Согласно определения предела функции при
Здесь нет сокращения на нуль, что никогда
не допустимо. Согласно определения предела функции при ![]() (опр.
1.5), аргумент
(опр.
1.5), аргумент ![]() стремится к своему предельному
значению
стремится к своему предельному
значению ![]() но
но ![]() Поэтому
здесь
Поэтому
здесь ![]()
Пример 5.1.
Найти 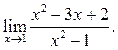
Решение.
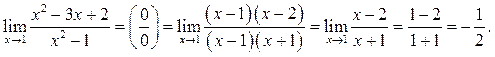
Напомним, что если числа ![]() и
и ![]() являются
корнями квадратного трехчлена
являются
корнями квадратного трехчлена ![]() то
то ![]()
Пример 5.2. Найти 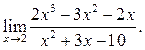
Решение.
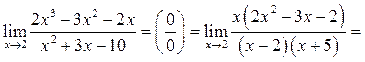
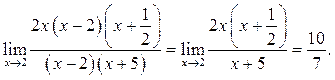
Пример 5.3. Найти 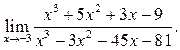
Решение. 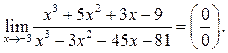 Для разложения выражений в числителе и
знаменателе на множители воспользуемся делением многочлена на многочлен:
Для разложения выражений в числителе и
знаменателе на множители воспользуемся делением многочлена на многочлен:
![]()
![]()
![]()
![]()
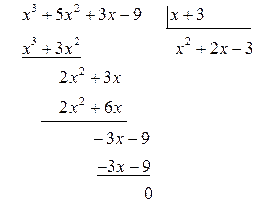
![]()
![]()
![]()
![]()
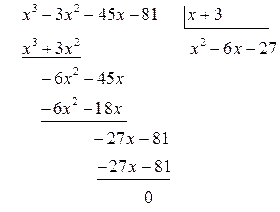
Таким образом,
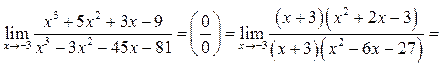
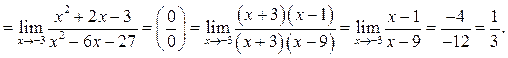
Пример 5.4. Найти 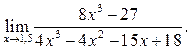
Решение.
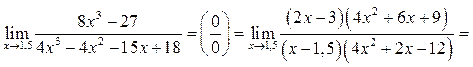
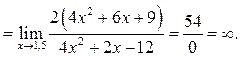
Пример 5.5.
Найти 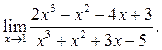
Решение.
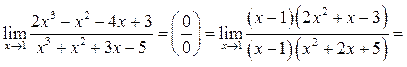
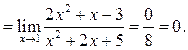
Если неопределенность ![]() выражена через иррациональные выражения,
то нужно путем преобразования избавиться от иррациональности и затем сократить
на множитель
выражена через иррациональные выражения,
то нужно путем преобразования избавиться от иррациональности и затем сократить
на множитель ![]()
Пример
5.6. Найти 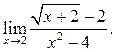
Решение.
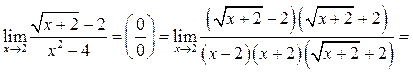
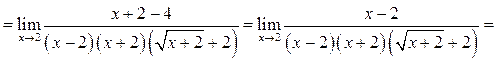
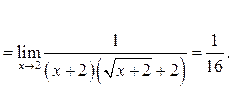
Пример
5.7. Найти 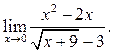
Решение.
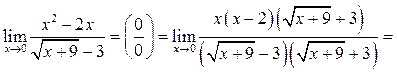
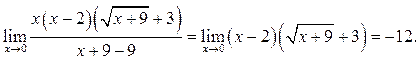
Пример
5.8. Найти 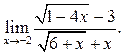
Решение.
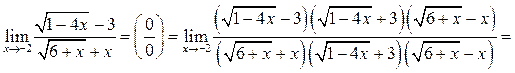
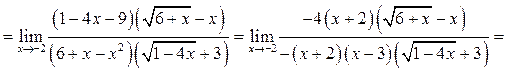
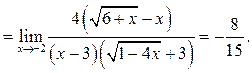
Пример 5.9.
Найти 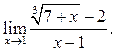
Решение.
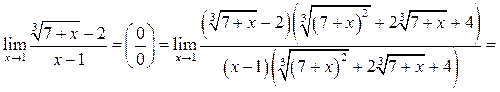
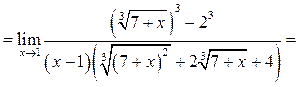
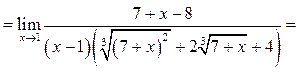
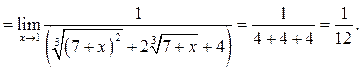
Пример 5.10.
Найти 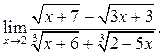
Решение.
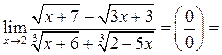
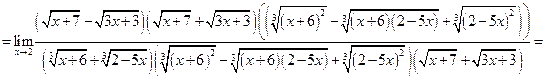
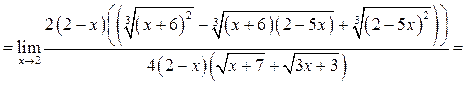
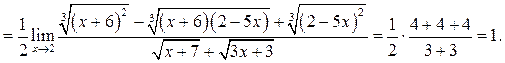
Пример 5.11. Найти
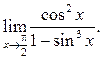
Решение.
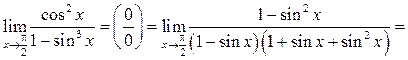
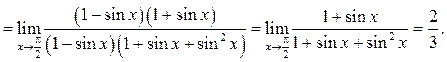
Пример 5.12.
Найти 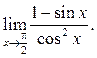
Решение.
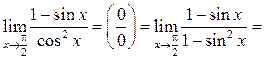
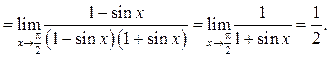
Задачи для самостоятельной работы
Найти пределы:
5.1 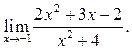 5.2
5.2 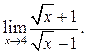 5.3
5.3 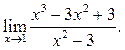
5.4 ![]() 5.5
5.5 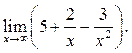 5.6
5.6 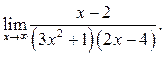
5.7 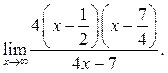 5.8
5.8 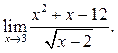 5.9
5.9 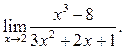
5.10 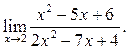 5.11
5.11 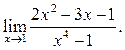 5.12
5.12 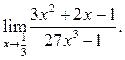
5.13 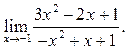 5.14
5.14 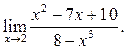 5.15
5.15 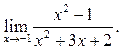
5.16 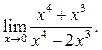 5.17
5.17 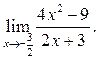 5.18
5.18 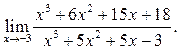
5.19 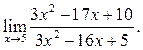 5.20
5.20 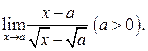 5.21
5.21 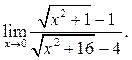 5.22
5.22
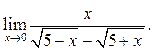 5.23
5.23 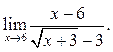 5.24
5.24
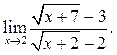
5.25 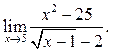 5.26
5.26 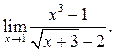 5.27
5.27 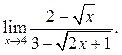
5.28 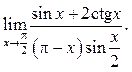 5.29
5.29 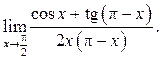 5.30
5.30 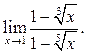
5.31 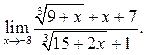 5.32
5.32 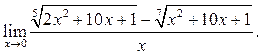
5.33 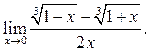 5.34
5.34 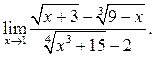
5.35 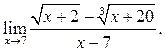 5.36
5.36 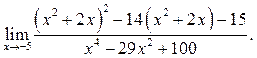
5.37 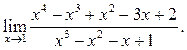 5.38
5.38 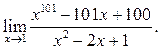
Если неопределенность ![]() получается при вычислении предела
отношения двух многочленов при
получается при вычислении предела
отношения двух многочленов при ![]() то нужно числитель и
знаменатель дроби разделить на старшую степень переменной.
то нужно числитель и
знаменатель дроби разделить на старшую степень переменной.
Пример 6.1. Найти 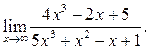
Решение.
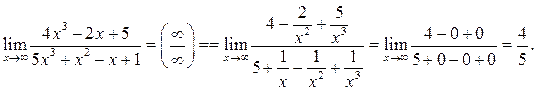
Пример 6.2. Найти 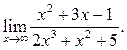
Решение.
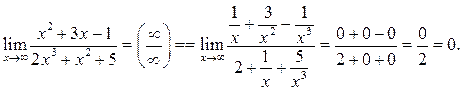
Пример 6.3. Найти 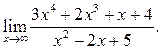
Решение.
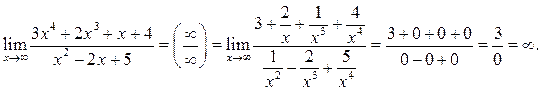
Из рассмотренных трех пределов можно вывести правило о пределе отношения двух многочленов.
Предел отношения двух многочленов
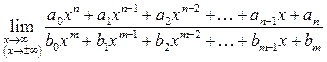
равен:
1)
![]() если
если ![]()
2)
![]() если
если ![]()
3)
![]() если
если ![]()
В дальнейшем будем пользоваться данным правилом.
Пример 6.4. Найти 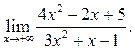
Решение. 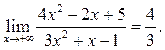
Пример 6.5. Найти 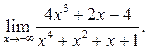
Решение. 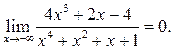
Рассмотрим другие случаи
раскрытия неопределенности ![]()
Пример 6.6. Найти 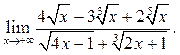
Решение. 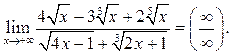 В подобных примерах полезно иметь в виду,
что функция
В подобных примерах полезно иметь в виду,
что функция ![]() где
где ![]() – многочлен
степени
– многочлен
степени ![]() стремится к бесконечности так же, как и
функция
стремится к бесконечности так же, как и
функция ![]() Это позволяет выделить высшую степень
Это позволяет выделить высшую степень ![]() входящую в данное выражение, и разделить
числитель и знаменатель на эту степень
входящую в данное выражение, и разделить
числитель и знаменатель на эту степень ![]() В
данном примере надо делить на
В
данном примере надо делить на ![]() тогда получим
тогда получим
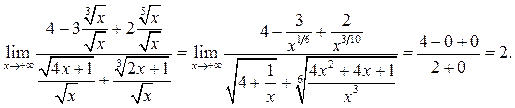
Пример 6.7. Найти 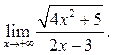
Решение.
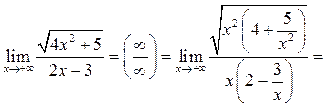
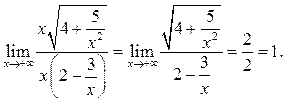
Здесь
использовано ![]() при
при ![]()
Пример 6.8. Найти 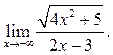
Решение.
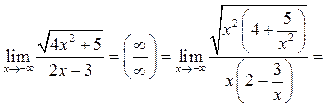
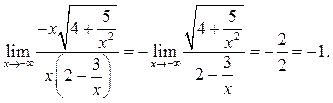
Здесь
использовано ![]() при
при ![]()
Пример 6.9. Найти 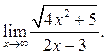
Решение. Предел 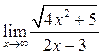 не существует, так как при
не существует, так как при ![]() и
и ![]() не
совпадают.
не
совпадают.
Рассмотрим неопределенность ![]()
Пример 6.10. Найти ![]()
Решение.
![]()
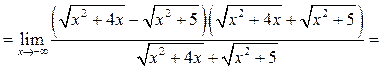
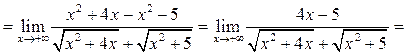
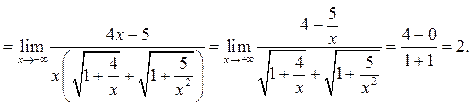
Пример 6.11.
Найти ![]()
Решение.
![]()
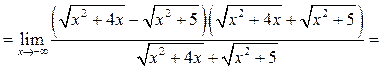
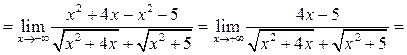
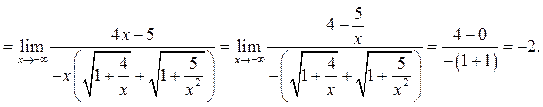
Здесь
использовано ![]() так как
так как ![]()
Пример 6.12. Найти ![]()
Решение.
![]()
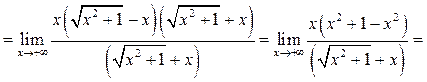
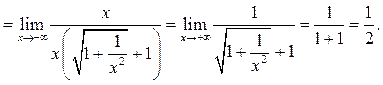
Пример 6.13. Найти ![]()
Решение.
![]()
Пример 6.14. Найти ![]()
Решение.
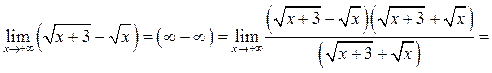
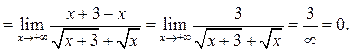
Пример 6.15. Найти ![]()
Решение.
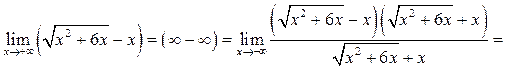
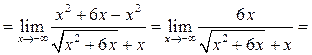
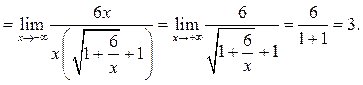
Пример 6.16. Найти ![]()
Решение. ![]()
Пример 6.17. Найти 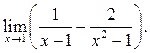
Решение.
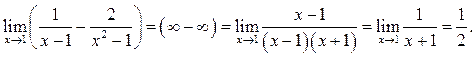
Пример 6.18. Найти 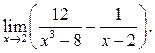
Решение.
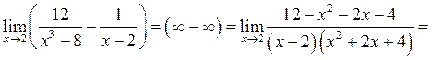
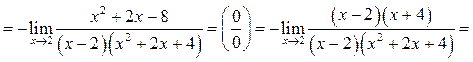
![]()
Пример 6.19. Найти 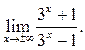
Решение.
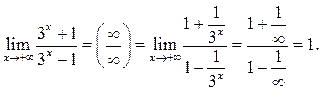
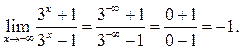
Пример 6.20. Найти 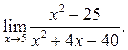
Решение. 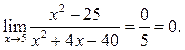
Последний пример
показывает, что при вычислении предела ![]() всегда
нужно начинать с прямой подстановки
всегда
нужно начинать с прямой подстановки ![]() Если неопределенности
нет, то результат получаем сразу, а при наличии неопределенности нужно
выполнять преобразования.
Если неопределенности
нет, то результат получаем сразу, а при наличии неопределенности нужно
выполнять преобразования.
Задачи для самостоятельной работы
Найти пределы:
6.1 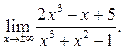 6.2
6.2 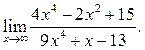 6.3
6.3 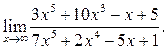
6.4 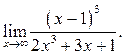 6.5
6.5 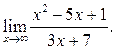 6.6
6.6 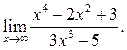
6.7 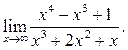 6.8
6.8 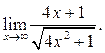 6.9
6.9 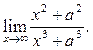
6.10 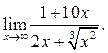 6.11
6.11 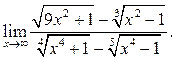 6.12
6.12 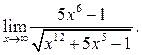
6.13 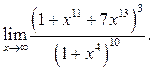 6.14
6.14
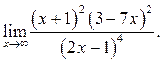
6.15 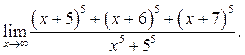 6.16
6.16
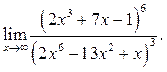
6.17 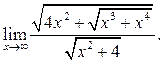 6.18
6.18
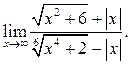
6.19 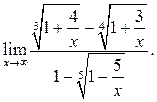 6.20
6.20
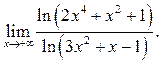
6.21 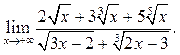 6.22
6.22
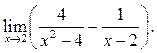
6.23 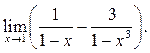 6.24
6.24
![]()
6.25 ![]() 6.26
6.26
![]()
6.27 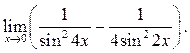 6.28
6.28
![]()
6.29 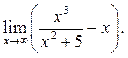 6.30
6.30
![]()
6.31 ![]() 6.32
6.32
![]()
6.33 ![]() 6.34
6.34
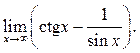
6.35 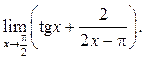 6.36
6.36
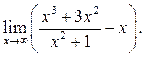
6.37 ![]()
6.38 ![]()
6.39 ![]()
6.40 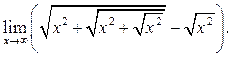
6.41 ![]()
6.42 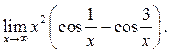
При вычислении пределов тригонометрических и обратных тригонометрических функций часто используется предел
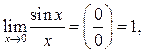 который
называется первым замечательным пределом. Часто этот предел используют в виде
который
называется первым замечательным пределом. Часто этот предел используют в виде
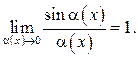
Очевидно, что
![]()
![]() (7.4)
(7.4)
Пример 7.1. Найти ![]()
Решение.
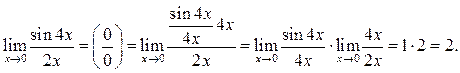
Пример 7.2. Найти ![]()
Решение.
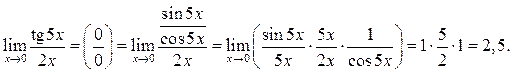
Пример 7.3. Найти 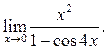
Решение.
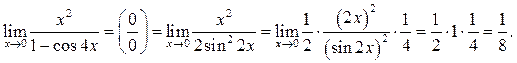
Пример 7.4. Найти 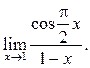
Решение.
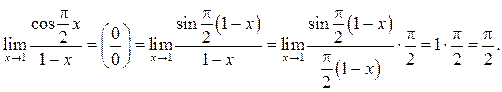
При вычислении таких пределов важно,
чтобы отношение функций было ![]() и неважно, что
и неважно, что ![]() (а не к нулю). Этот предел можно вычислить
с помощью замены переменной
(а не к нулю). Этот предел можно вычислить
с помощью замены переменной ![]() при
при ![]() Тогда
Тогда
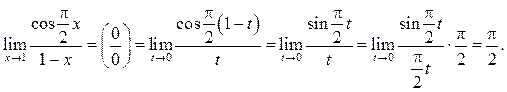
Пример 7.5. Найти ![]()
Решение.
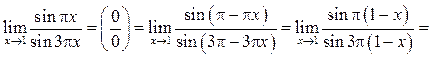
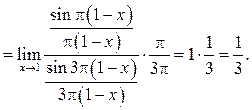
Пример 7.6. Найти ![]()
Решение.
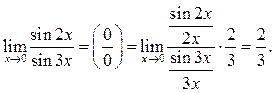
Пример 7.7. Найти ![]()
Решение.
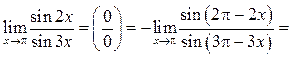
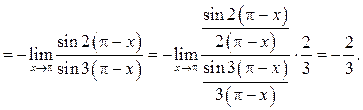
Здесь нельзя было воспользоваться преобразованием примера
7.6, так как при ![]() выражения
выражения ![]() и
и ![]() не
являются бесконечно малыми.
не
являются бесконечно малыми.
Пример 7.8. Найти ![]()
Решение.
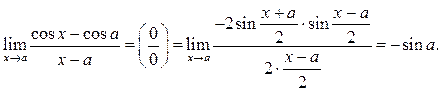
Пример 7.9. Найти ![]()
Решение. Применим подстановку ![]()
![]() при
при
![]() Тогда
Тогда
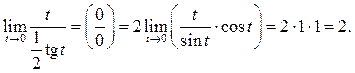
Пример 7.10. Найти 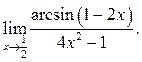
Решение.
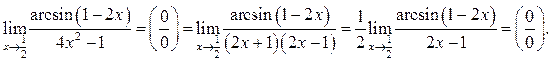
Применим подстановку ![]()
![]() при
при ![]() Тогда имеем
Тогда имеем ![]()
Пример 7.11 Найти 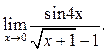
Решение.
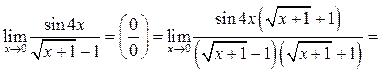
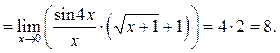
Пример 7.12. Найти ![]()
Решение. ![]() так
как данный предел представляет собою отношение ограниченной функции
так
как данный предел представляет собою отношение ограниченной функции ![]() при
при ![]() к бесконечно большой функции
к бесконечно большой функции ![]() равное
бесконечно малой функции.
равное
бесконечно малой функции.
Пример 7.13. Найти ![]()
Решение.
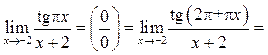
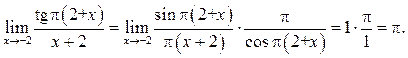
Пример 7.14. Найти ![]()
Решение.
![]()
Пример 7.15. Найти ![]()
Решение.
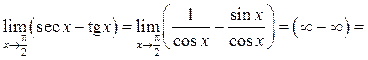
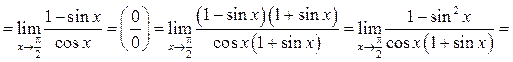
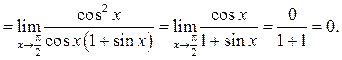
Задачи для самостоятельной работы
Найти пределы:
7.1
![]() 7.2
7.2 ![]() 7.3
7.3 ![]()
7.4
![]() 7.5
7.5 ![]() 7.6
7.6 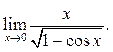
7.7
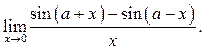 7.8
7.8 ![]() 7.9
7.9 ![]()
7.10
![]() 7.11
7.11 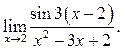 7.12
7.12 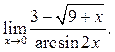
7.13
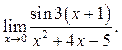 7.14
7.14 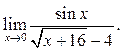 7.15
7.15 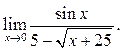
7.16
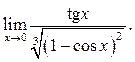 7.17
7.17 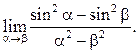 7.18
7.18 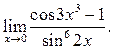
7.19
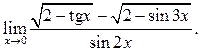 7.20
7.20 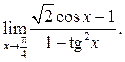
Предел
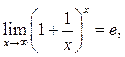 или
или
![]() называется вторым замечательным
пределом.
называется вторым замечательным
пределом.
Лучше использовать эти пределы в такой форме
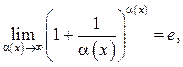 или
или
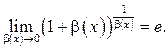
С помощью второго
замечательного предела раскрывается неопределенность ![]()
Пример 8.1. Найти 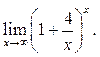
Решение.
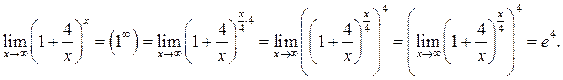
Пример 8.2. Найти ![]()
Решение.
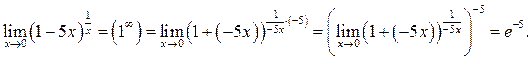
С учетом результатов примеров 8.1 и 8.2 можно использовать формулы
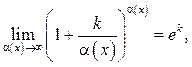 (8.5)
(8.5)
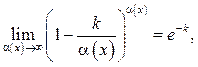 (8.6)
(8.6)
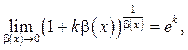 (8.7)
(8.7)
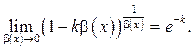 (8.8)
(8.8)
Здесь ![]() – число (не обязательно целое).
– число (не обязательно целое).
Пример 8.3. Найти 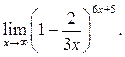
Решение.
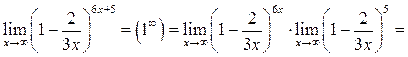
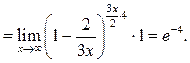
Пример 8.4. Найти 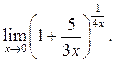
Решение.
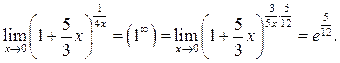
Пример 8.5. Найти 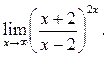
Решение.
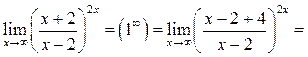
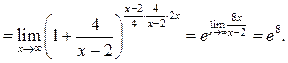
Пример 8.6. Найти 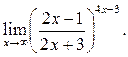
Решение.
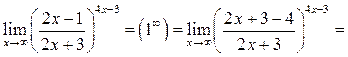
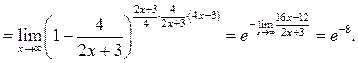
Рассмотрим второй способ вычисления данного предела.
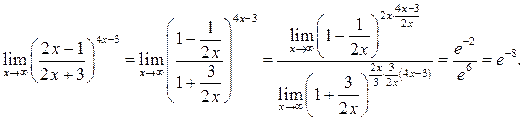
Пример 8.7. Найти 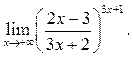
Решение.
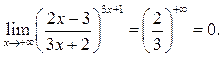
Пример 8.8. Найти 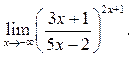
Решение.
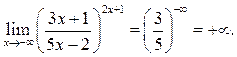
Пример 8.9. Найти ![]()
Решение.
![]()
Пример 8.10. Найти ![]()
Решение.
![]()
Пример 8.11. Найти 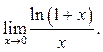
Решение.
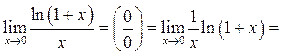
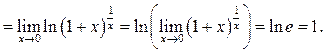
Пример 8.12. Найти ![]()
Решение.
![]()
Пример 8.13. Найти 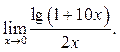
Решение.
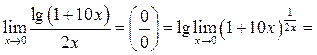
![]()
Рассмотрим нахождение пределов вида в общем случае
![]()
1 Можно воспользоваться формулой
![]()
2
Если существуют конечные пределы ![]() и
и
![]() то
то ![]()
3
Если ![]() то
нужно воспользоваться П1 и П2 из третьего раздела.
то
нужно воспользоваться П1 и П2 из третьего раздела.
4
Если ![]() и
и ![]() то нужно положить
то нужно положить ![]() где
где
![]() при
при ![]() и,
следовательно,
и,
следовательно,
![]()
Некоторые из этих преобразований мы уже использовали.
Пример 8.14. Найти ![]()
Решение.
![]()
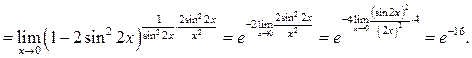
Пример 8.15. Найти 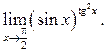
Решение.
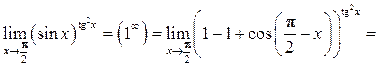
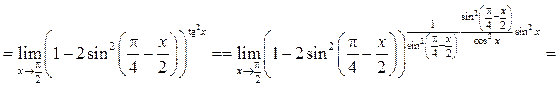
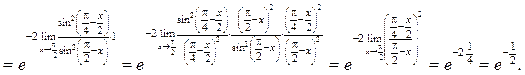
Задачи для самостоятельной работы
Найти пределы:
8.1
![]() 8.2
8.2 ![]() 8.3
8.3 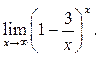
8.4
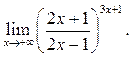 8.5
8.5 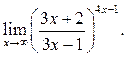 8.6
8.6 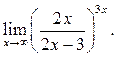
8.7
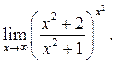 8.8
8.8 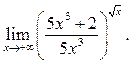 8.9
8.9 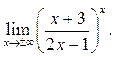
8.10
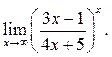 8.11
8.11 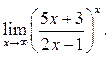 8.12
8.12
![]()
8.13
![]() 8.14
8.14 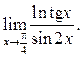 8.15
8.15 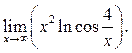
8.16
![]() 8.17
8.17 ![]() 8.18
8.18 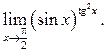
8.19
![]() 8.20
8.20 ![]() 8.21
8.21
![]()
8.22
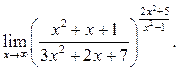 8.23
8.23 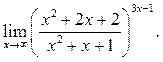
8.24
![]() 8.25
8.25 ![]()
Пример 9.1. Найти: а) 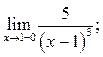 б)
б) 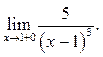
Решение.
а) При ![]() поэтому
поэтому ![]() и б. м. ф., тогда
и б. м. ф., тогда ![]() –
отрицательная б. м. ф., т. е.
–
отрицательная б. м. ф., т. е. 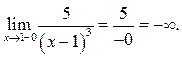
б) При ![]() поэтому
поэтому ![]() и б. м. ф., тогда
и б. м. ф., тогда ![]() –
положительная б. м. ф., т. е.
–
положительная б. м. ф., т. е. 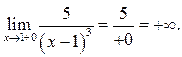
Пример 9.2. Найти: а) ![]() б)
б) ![]()
Решение.
![]()
Пример 9.3. Найти: а) ![]() б)
б) ![]()
Решение.
![]()
![]()
Пример 9.4. Найти: а) 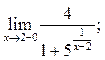 б)
б) 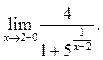
Решение.
а) При ![]() и тогда
имеем:
и тогда
имеем:
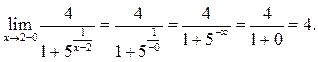
б)
При ![]() и тогда
имеем:
и тогда
имеем:
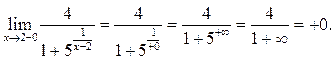
Пример 9.5. Найти 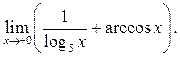
Решение. ![]() тогда
тогда
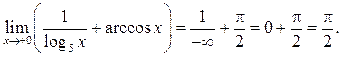
Пример 9.6. Найти а) ![]() б)
б) ![]()
Решение.
![]()
![]()
Задачи для самостоятельной работы
Вычислить односторонние пределы функций:
9.1
![]() 9.2
9.2 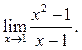 9.3
9.3 ![]() 9.4
9.4 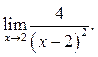
9.5
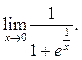 9.6
9.6 ![]() 9.7
9.7 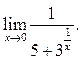 9.8
9.8 ![]()
9.9
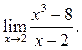 9.10
9.10 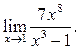 9.11
9.11 ![]() 9.12
9.12 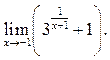
Смешанные примеры на вычисление пределов для самостоятельной работы
Найти пределы:
9.13
![]() 9.14
9.14 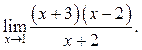 9.15
9.15 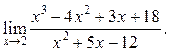
9.16
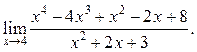 9.17
9.17 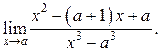
9.18
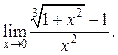 9.19
9.19 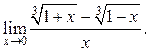 9.20
9.20
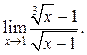
9.21
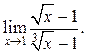 9.22
9.22 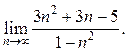 9.23
9.23
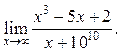
9.24
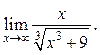 9.25
9.25 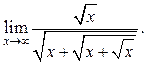 9.26
9.26
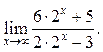
9.27 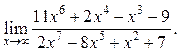 9.28
9.28
![]()
9.29 ![]() 9.30
9.30
![]()
9.31 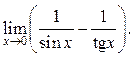 9.32
9.32
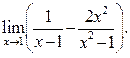 9.33
9.33 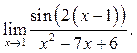 9.34
9.34 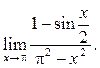 9.35
9.35
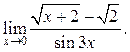 9.36
9.36 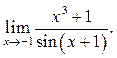
9.37 ![]() 9.38
9.38
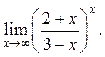 9.39
9.39 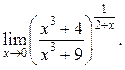
9.40 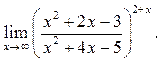 9.41
9.41
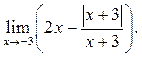 9.42
9.42 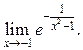
Бесконечно малые функции ![]() и
и ![]() называются эквивалентными (равносильными)
при
называются эквивалентными (равносильными)
при ![]() если
если 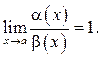
Эквивалентность обозначается символом ![]() т. е.
пишут
т. е.
пишут ![]()
Если ![]() – бесконечно малая функция, то справедливы
основные эквивалентности:
– бесконечно малая функция, то справедливы
основные эквивалентности:
![]()
![]() (10.2)
(10.2)
![]() (10.3)
(10.3)
![]() (10.4)
(10.4)
![]() (10.5)
(10.5)
![]() (10.6)
(10.6)
![]() (10.7)
(10.7)
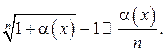 (10.8)
(10.8)
При вычислении пределов используются следующие теоремы об эквивалентных бесконечно малых функциях:
Т1. Предел отношения двух бесконечно малых функций равен пределу отношения функций, им эквивалентных.
Т2. Сумма нескольких бесконечно малых функций различных порядков малости эквивалентна слагаемому низшего порядка малости.
Пример 10.1. Найти 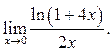
Решение.
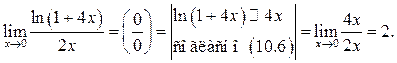
Пример 10.2. Найти 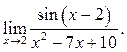
Решение.
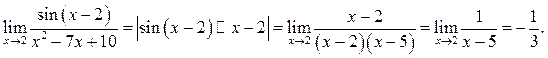
Пример 10.3. Найти ![]()
Решение.
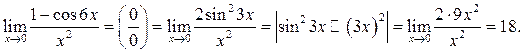
Пример 10.4. Найти 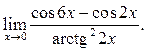
Решение.
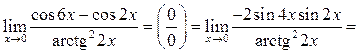
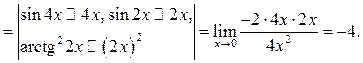
Пример 10.5. Найти ![]()
Решение.
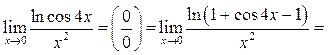
![]()
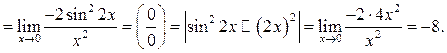
Пример 10.6. Найти 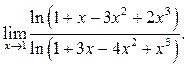
Решение. Так
как при ![]() и
и ![]() то по
формуле (10.6)
то по
формуле (10.6)
![]()
Получаем
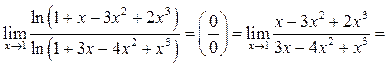
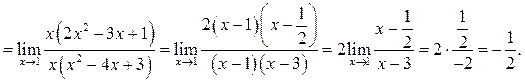
Пример 10.7. Найти ![]()
Решение. Здесь
числитель и знаменатель – б. м. ф. Однако ![]() не
является бесконечно малой функцией и ошибкой было бы соотношение
не
является бесконечно малой функцией и ошибкой было бы соотношение ![]() Сделаем замену переменной
Сделаем замену переменной ![]() тогда при
тогда при ![]()
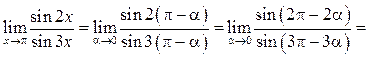
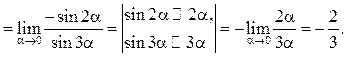
Пример 10.8. Найти 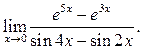
Решение.
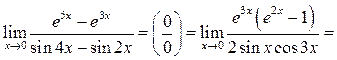
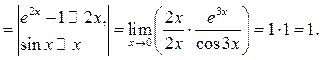
Пример 10.9. Найти 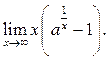
Решение.
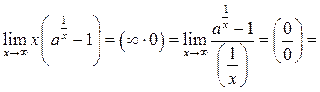
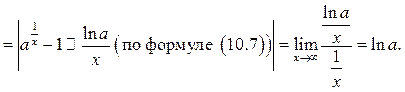
Пример 10.10. Найти 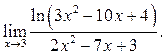
Решение.
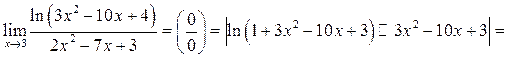
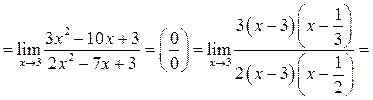
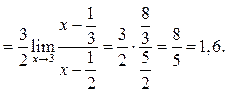
Пример 10.11. Найти 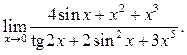
Решение.
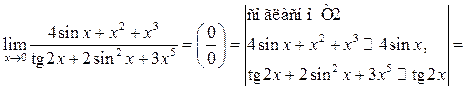
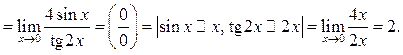
Пример 10.12. Найти ![]()
Решение.
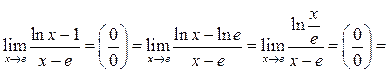
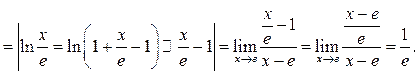
Пример 10.13. Найти 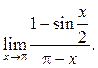
Решение.
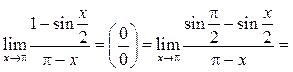
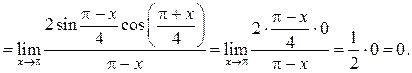
Пример 10.14. Найти 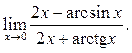
Решение.
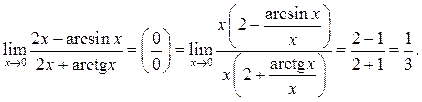
Задачи для самостоятельной работы
Найти пределы:
10.1 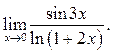 10.2
10.2
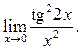 10.3
10.3 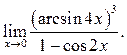
10.4 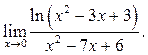 10.5
10.5 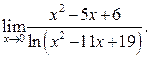 10.6
10.6 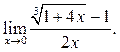
10.7 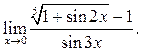 10.8
10.8
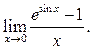 10.9
10.9 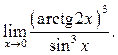
10.10 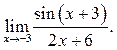 10.11
10.11
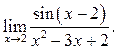 10.12
10.12 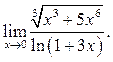
10.13 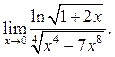 10.14
10.14
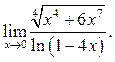 10.15
10.15 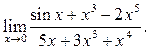 10.16
10.16
![]() 10.17
10.17 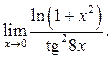 10.18
10.18
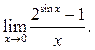 10.19
10.19 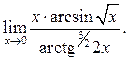 10.20
10.20
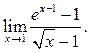 10.21
10.21 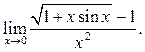
10.22 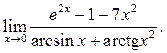 10.23
10.23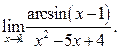 10.24
10.24![]()
Найти пределы функций.
Вариант 1
1
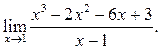 2.
2. 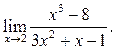 3
3 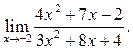
4
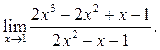 5
5 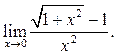
Вариант 2
1
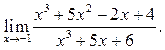 2
2 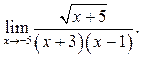 3
3 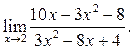
4
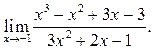 5
5 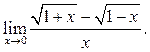
Вариант 3
1
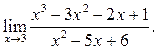 2
2 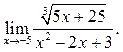 3
3 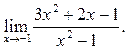
4
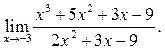 5
5 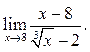
Вариант 4
1
![]() 2
2 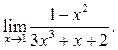 3
3 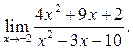
4
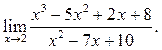 5
5 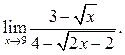
Вариант 5
1 ![]() 2
2 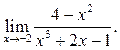 3
3 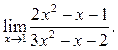
4 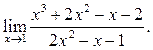 5
5 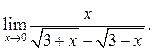
Вариант 6
1 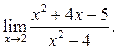 2
2 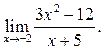 3
3 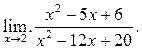
4 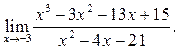 5
5 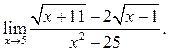
Вариант 7
1 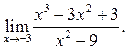 2
2 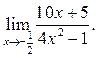 3
3 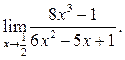
4 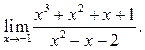 5
5 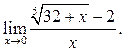
Вариант 8
1 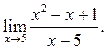 2
2 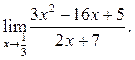 3
3 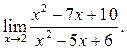
4 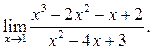 5
5 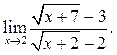
Вариант 9
1 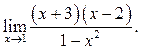 2
2 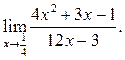 3
3 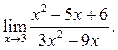
4 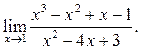 5
5 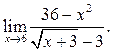
Вариант 10
1 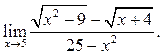 2
2 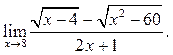 3
3 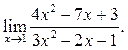
4 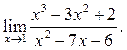 5
5 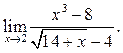
Найти пределы функций.
Вариант 1
1 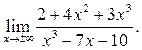 2
2 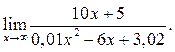 3
3 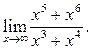
4 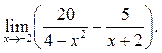 5
5 ![]() 6
6 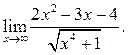
Вариант 2
1 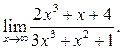 2
2 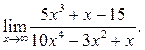 3
3 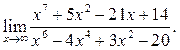
4 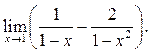 5
5 ![]() 6
6 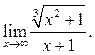
Вариант 3
1 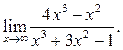 2
2 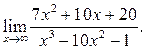 3
3 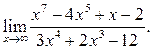
4 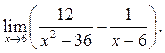 5
5 ![]() 6
6 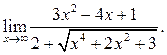
Вариант 4
1 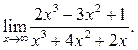 2
2 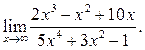 3
3 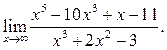
4 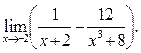 5
5 ![]() 6
6 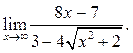
Вариант 5
1 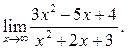 2
2 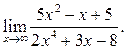 3
3 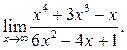
4 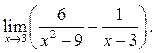 5
5 ![]() 6
6 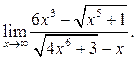
Вариант 6
1 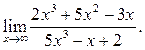 2
2 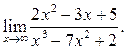 3
3 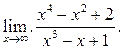
4 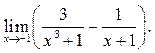 5
5 ![]() 6
6 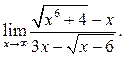
Вариант 7
1 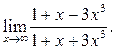 2
2 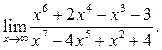 3
3 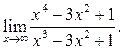
4 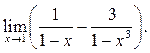 5
5 ![]() 6
6 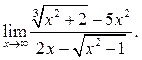
Вариант 8
1 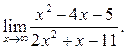 2
2 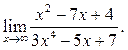 3
3 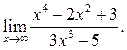
4 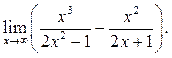 5
5 ![]() 6
6 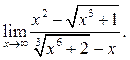
Вариант 9
1 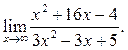 2
2 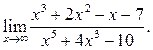 3
3 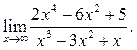
4 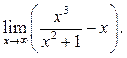 5
5 ![]() 6
6 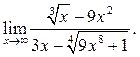
Вариант 10
1 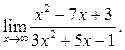 2
2 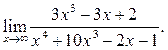 3
3 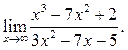
4 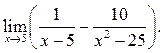 5
5 ![]() 6
6 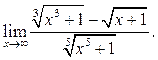
Найти пределы функций, применяя первый замечательный предел.
Вариант 1
1 ![]() 2
2 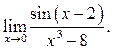 3
3 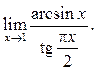
Вариант 2
1 ![]() 2
2 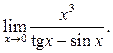 3
3 ![]()
Вариант 3
1 ![]() 2
2 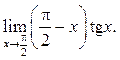 3
3 ![]()
Вариант 4
1 ![]() 2
2 ![]() 3
3 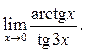
Вариант 5
1 ![]() 2
2 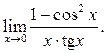 3
3 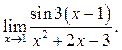
Вариант 6
1 ![]() 2
2 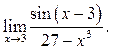 3
3 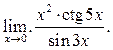
Вариант 7
1 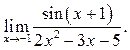 2
2 ![]() 3
3 ![]()
Вариант 8
1 ![]() 2
2 ![]() 3
3 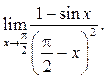
Вариант 9
1 ![]() 2
2 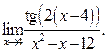 3
3 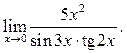
Вариант 10
1 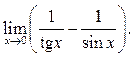 2
2 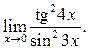 3
3 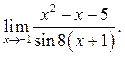
Найти пределы функций, применяя второй замечательный предел.
Вариант 1
1 ![]() 2
2 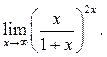 3
3 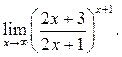
4 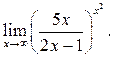 5
5 ![]() 6
6 ![]()
Вариант 2
1 ![]() 2
2 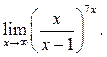 3
3 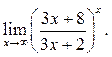
4 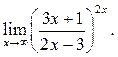 5
5 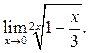 6
6 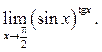
Вариант 3
1 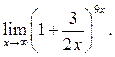 2
2 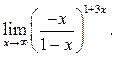 3
3 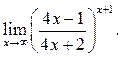
4 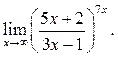 5
5 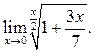 6
6 ![]()
Вариант 4
1 ![]() 2
2 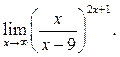 3
3 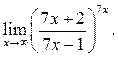
4 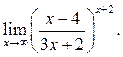 5
5 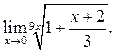 6
6 ![]()
Вариант 5
1 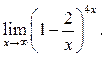 2
2 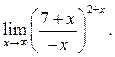 3
3 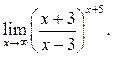
4 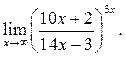 5
5 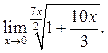 6
6 ![]()
Вариант 6
1 ![]() 2
2 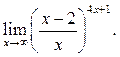 3
3 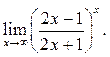
4 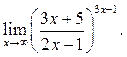 5
5 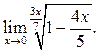 6
6 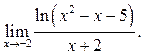
Вариант 7
1 ![]() 2
2 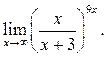 3
3 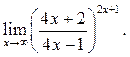
4 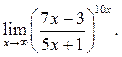 5
5 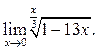 6
6 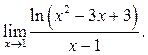
Вариант 8
1 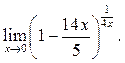 2
2 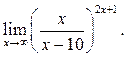 3
3 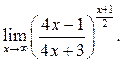
4 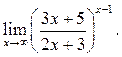 5
5 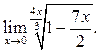 6
6 ![]()
Вариант 9
1
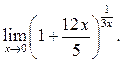 2
2 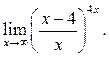 3
3 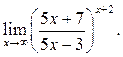
4 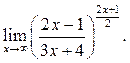 5
5 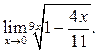 6
6 ![]()
Вариант 10
1 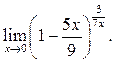 2
2 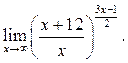 3
3 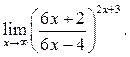
4 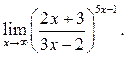 5
5 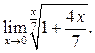 6
6 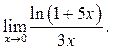
Найти пределы функций c помощью формул эквивалентности.
Вариант 1
1 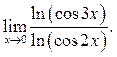 2
2 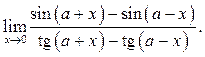 3
3 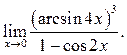
Вариант 2
1 ![]() 2
2 ![]() 3
3 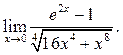
Вариант 3
1 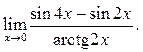 2
2 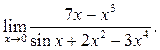 3
3 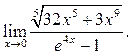
Вариант 4
1
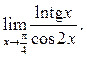 2
2 ![]() 3
3 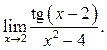
Вариант 5
1
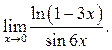 2
2 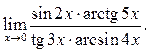 3
3 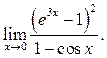
Вариант 6
1
![]() 2
2 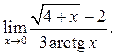 3
3 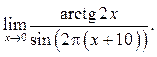
Вариант 7
1 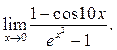 2
2 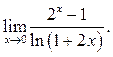 3
3 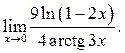
Вариант 8
1 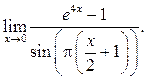 2
2 ![]() 3
3 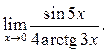
Вариант 9
1 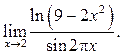 2
2 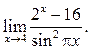 3
3 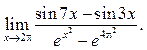
Вариант 10
1 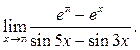 2
2 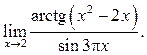 3
3 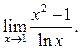
Найти односторонние пределы в пунктах 1) и 2). Исследовать на непрерывность функцию в пункте 3).
Вариант 1
1 ![]() 2
2 ![]() 3
3 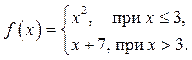
Вариант 2
1 ![]() 2
2 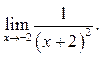 3
3 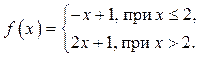
Вариант 3
1 ![]() 2
2 ![]() 3
3 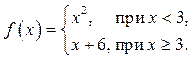
Вариант 4
1 ![]() 2
2 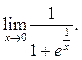 3
3 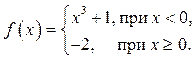
Вариант 5
1 ![]() 2
2 ![]() 3
3 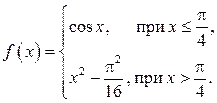
Вариант 6
1 ![]() 2
2 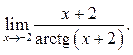 3
3 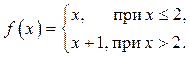
Вариант 7
1 ![]() 2
2 ![]() 3
3 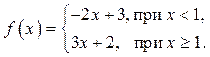
Вариант 8
1 ![]() 2
2 ![]() 3
3 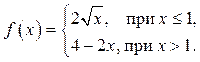
Вариант 9
1  2
2 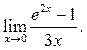 3
3 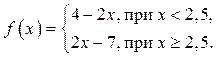
Вариант 10
1 ![]() 2
2 ![]() 3
3 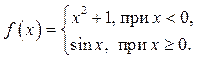
Каждый вариант контрольной работы состоит из тринадцати заданий, в которых необходимо:
1)
в заданиях ![]() найти
указанные пределы;
найти
указанные пределы;
2)
в задании 10 доказать, что функции
![]() и
и ![]() при
при ![]() являются бесконечно малыми одного порядка;
являются бесконечно малыми одного порядка;
3) в задании 11 найти пределы, используя эквивалентные бесконечно малые функции;
4) в задании 12 исследовать данные функции на непрерывность в указанных точках;
5) в задании 13 исследовать данные функции на непрерывность, построить их графики.
Вариант 1
1
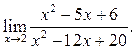 2
2 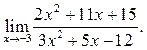 3
3 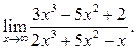
4
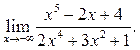 5
5 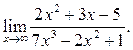 6
6 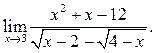
7
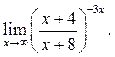 8
8 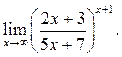 9
9 ![]()
10
![]() 11
11 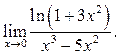
12
![]() 13
13 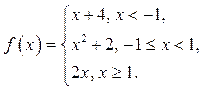
Вариант 2
1
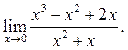 2
2 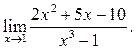 3
3 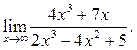
4
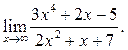 5
5 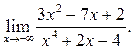 6
6 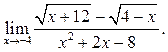
7
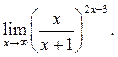 8
8 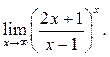 9
9 ![]()
10
![]() 11
11 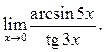
12
![]() 13
13 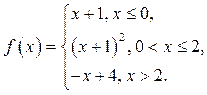
Вариант 3
1
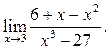 2
2 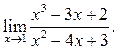 3
3 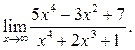
4
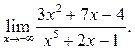 5
5 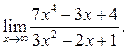 6
6 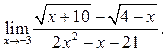
7
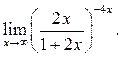 8
8 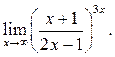 9
9 ![]()
10
![]() 11
11 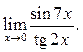
12
![]() 13
13 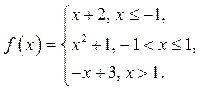
Вариант 4
1
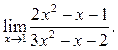 2
2 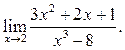 3
3 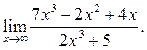
4
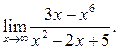 5
5 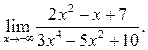 6
6 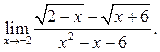
7
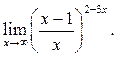 8
8 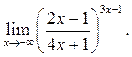 9
9 ![]()
10
![]() 11
11 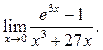
12
![]() 13
13 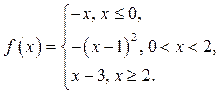
Вариант 5
1
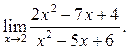 2
2 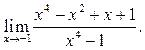 3
3 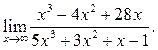
4
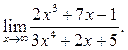 5
5 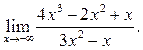 6
6 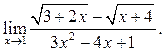
7
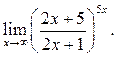 8
8 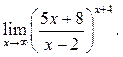 9
9 ![]()
10
![]() 11
11 ![]()
12
![]() 13
13 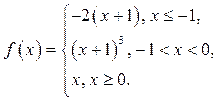
Вариант 6
1
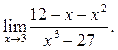 2
2 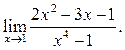 3
3 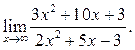
4
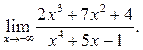 5
5 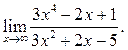 6
6 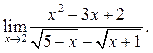
7
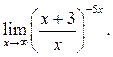 8
8 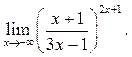 9
9 ![]()
10
![]() 11
11 ![]()
12
![]() 13
13 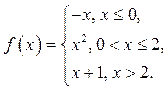
Вариант 7
1
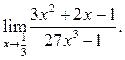 2
2 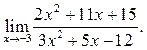 3
3 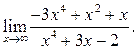
4
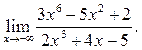 5
5 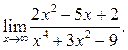 6
6 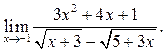
7
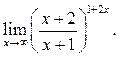 8
8 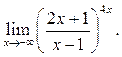 9
9 ![]()
10
![]() 11
11 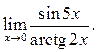
12
![]() 13
13 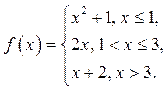
Вариант 8
1
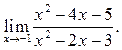 2
2 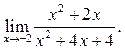 3
3 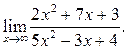
4
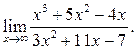 5
5 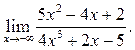 6
6 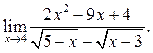
7
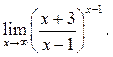 8
8 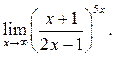 9
9 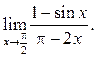
10
![]() 11
11 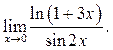
12
![]() 13
13 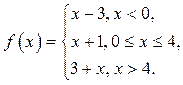
Вариант 9
1
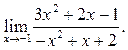 2
2 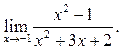 3
3 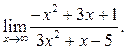
4
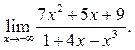 5
5 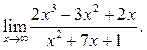 6
6 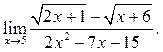
7
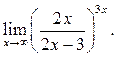 8
8 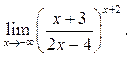 9
9 ![]()
10
![]() 11
11 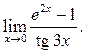
12
![]() 13
13 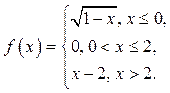
Вариант 10
1
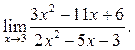 2
2 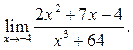 3
3 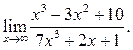
4
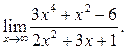 5
5 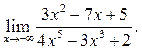 6
6 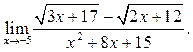
7
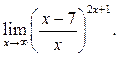 8
8 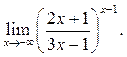 9
9 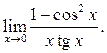
10
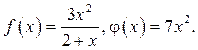 11
11 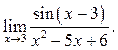
12
![]() 13
13 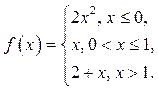
Вариант 11
1
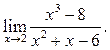 2
2 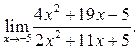 3
3 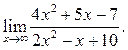
4
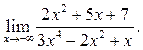 5
5 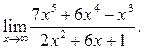 6
6 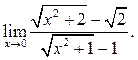
7
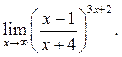 8
8 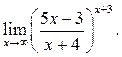 9
9 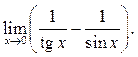
10
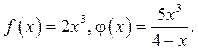 11
11 ![]()
12
![]() 13
13 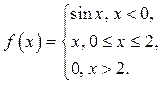
Вариант 12
1
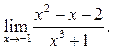 2
2 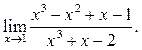 3
3 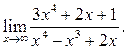
4
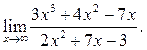 5
5 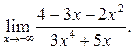 6
6 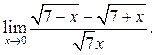
7
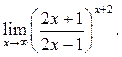 8
8 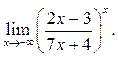 9
9 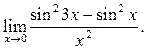
10
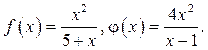 11
11 ![]()
12
![]() 13
13 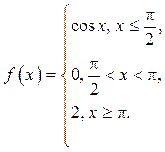
Вариант 13
1
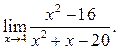 2
2 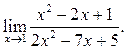 3
3 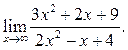
4
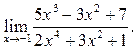 5
5 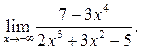 6
6 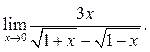
7
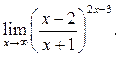 8
8 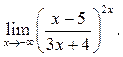 9
9 ![]()
10
![]() 11
11 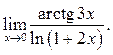
12
![]() 13
13 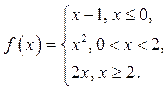
Вариант 14
1
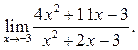 2
2 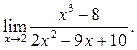 3
3 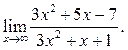
4
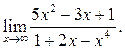 5
5 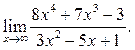 6
6 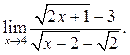
7
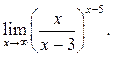 8
8 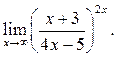 9
9 ![]()
10
![]() 11
11 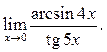
12
![]() 13
13 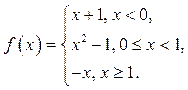
Вариант 15
1
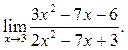 2
2 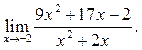 3
3 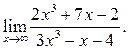
4
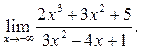 5
5 ![]() 6
6 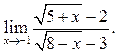
7
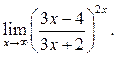 8
8 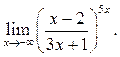 9
9 ![]()
10
![]() 11
11 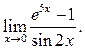
12
![]() 13
13 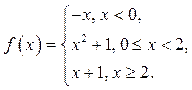
ОГЛАВЛЕНИЕ
1 Определение пределов функций….…………………………………………………..... 3
2 Бесконечно малые и бесконечно большие функции…..……............................…..….. 7
3 Основные теоремы о пределах…………………………………………………………. 11
4 Неопределенные выражения…………………………………………………………… 13
5 Раскрытие
неопределенностей вида ![]() ……………….……..…….………………….. 14
……………….……..…….………………….. 14
6 Раскрытие
неопределенностей вида ![]() и
и ![]() ……..……….……………………. 21
……..……….……………………. 21
7 Первый замечательный предел……………………………………………………….... 30
8 Второй замечательный предел………………………………………………………..... 36
9 Вычисление односторонних пределов……………………………………………....... 42
10 Применение эквивалентных бесконечно малых к вычислению пределов…….….. 46
Самостоятельная работа № 1……………………………………………………….….… 53
Самостоятельная работа № 2…………………………………………………….….…… 55
Самостоятельная работа № 3…………………………………………………….….…… 57
Самостоятельная работа № 4…………………………………………………….….…… 58
Самостоятельная работа № 5…………………………………………………….….…… 61
Самостоятельная работа № 6…………………………………………………….….…… 62
Контрольная работа…………………………………………………………….….……… 65
Щ66
Р е ц е н з е н т : канд. физ.-мат. наук, доцент кафедры высшей математики
А. Д. Суворова (УО «БелГУТ»).
Щербо, А. М.
Щ66 Пределы : учеб.-метод. пособие / А. М. Щербо, И. П. Шабалина,
Л. В. Головач ; М-во образования Респ. Беларусь, Белорус. гос. ун-т трансп. – Гомель : УО БелГУТ, 2007. – 71 с.
ISBN 978-985-468-330-0
Рассмотрены основные методы вычисления пределов. Излагаемый теоретический материал сопровождается большим количеством примеров с подробными пояснениями, что существенно облегчает усвоение основных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.