





Балтийский государственный технический
университет имени Д.Ф.Устинова.
Кафедра «Сопротивление материалов».
Курсовая работа по сопротивлению материалов.
Расчёт пространственной стержневой системы.
Выполнил: ИвАнов Д.А.
Группа М122
Преподаватель: Буткарева Н.Г.
Санкт-Петербург
2005
Геометрические размеры и величины приняты следующими: b=25мм, h=35мм, 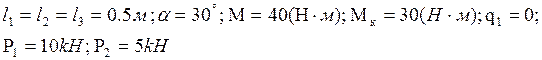
1.Определение геометрических характеристик.
Сечение А (круглое): 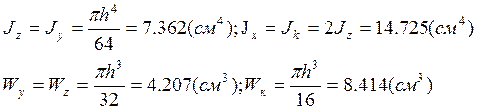
Сечение Б (прямоугольное): 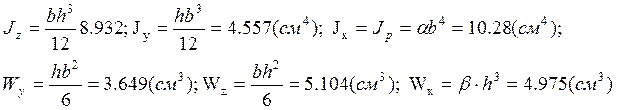
Коэффициент ![]() находим по формуле (
находим по формуле (![]() берём из табл. приложения4 на стр.355
пособия)
берём из табл. приложения4 на стр.355
пособия) 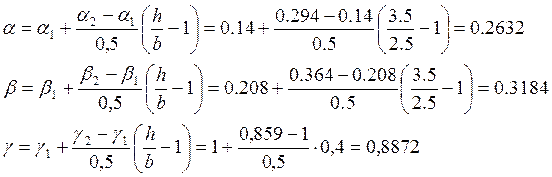
Сечение В (кольцо): 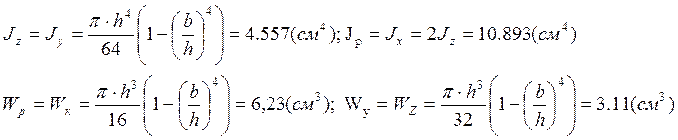
Сложное сечение. Моменты инерции определим аналитически. 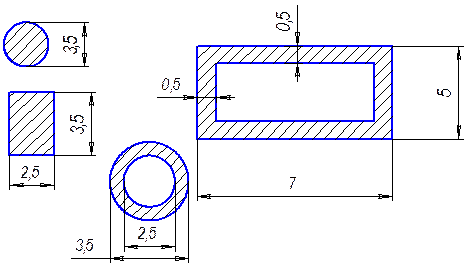
b=5см, h=7см,![]() .
.
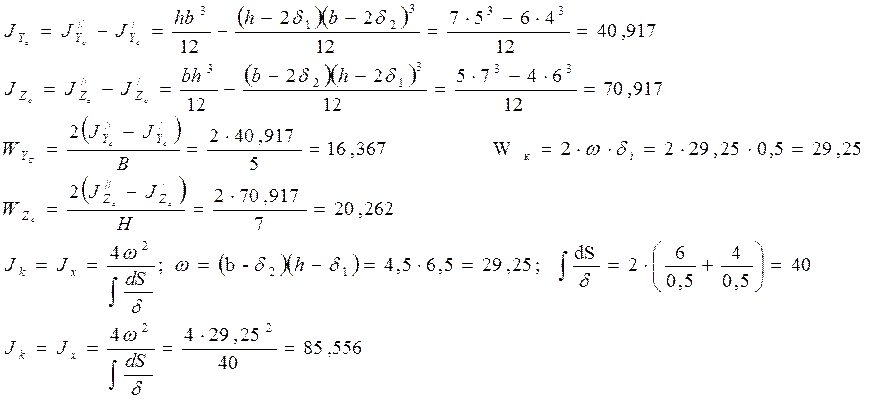
2.Определение направляющих косинусов. С целью определения направляющих косинусов стержневой системы вычерчиваем в масштабе в трёх проекциях. Ориентацию сечений указываем соответственно направлениям локальных осей. Углы, соответствующие направляющим косинусам, согласно принятым обозначениям, заносим в таблицу. В ней же указываем длины и площади элементов.
|
№ |
Углы, соответствующие направляющим косинусам |
длина L, см |
площадь F, см*см |
||||||||
|
xX |
xY |
xZ |
yX |
yY |
yZ |
zX |
zY |
zZ |
|||
|
I |
90 |
120 |
30 |
180 |
90 |
90 |
90 |
150 |
120 |
56 |
9,616 |
|
II |
45 |
90 |
45 |
90 |
0 |
90 |
135 |
90 |
45 |
71 |
9,616 |
|
III |
0 |
90 |
90 |
90 |
0 |
90 |
90 |
90 |
0 |
50 |
9,616 |
|
IV |
90 |
90 |
0 |
90 |
0 |
90 |
180 |
90 |
90 |
50 |
8,75 |
|
V |
90 |
135 |
45 |
180 |
90 |
90 |
90 |
135 |
135 |
71 |
4,712 |
|
VI |
30 |
120 |
90 |
90 |
90 |
0 |
135 |
135 |
90 |
56 |
8,75 |
|
VII |
0 |
90 |
90 |
90 |
90 |
0 |
90 |
180 |
90 |
50 |
11 |
|
VIII |
30 |
60 |
90 |
90 |
90 |
0 |
60 |
150 |
90 |
28 |
4,712 |
|
IX |
30 |
60 |
90 |
90 |
90 |
0 |
60 |
150 |
90 |
28 |
4,712 |
|
X |
90 |
180 |
90 |
90 |
90 |
0 |
180 |
90 |
90 |
25 |
8,75 |
|
XI |
90 |
180 |
90 |
90 |
90 |
0 |
180 |
90 |
90 |
25 |
8,75 |
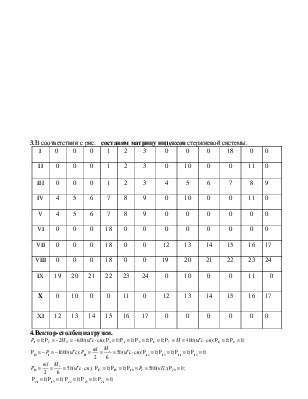
3.В соответствии с рис. составим матрицу индексов стержневой системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.