Расчет переходного процесса (E=150 В, L=0,08 Гн, R1=40 Ом, R2=160 Ом, R3=200 Ом, C=4 мкФ, ключ замыкается)

                                      Содержание:

1.  Электрическая схема рассчитываемой цепи----------------------------------3

2.  Расчет принужденного режима--------------------------------------------------3

3.  Составление дифференциального уравнения---------------------------------3

4.  Решение дифференциального уравнения--------------------------------------5

5.  Определение остальных токов и напряжений в электрической цепи----8

6.  Операторный метод расчета электрической цепи----------------------------8

7.  Сравнение результатов-----------------------------------------------------------11

8.  Графики токов и напряжений---------------------------------------------------11

9.  Заключение-------------------------------------------------------------------------12

10.Список использованной литературы------------------------------------------14

1. Электрическая схема рассчитываемой цепи.

В цепи, изображенной на рис. 1, происходит коммутация в момент времени t= 0 (ключ замыкается). Параметры схемы: L= 0.08 Гн,  R₁= 40 Ом, R₂=160 Ом, R₃=200 Ом, С=4*10^-6 Ф, Е=150 В.

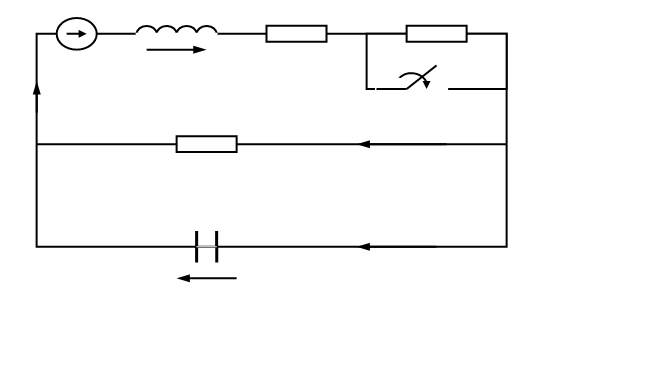+Рис. 1. Электрическая схема рассчитываемой цепи.

2. Расчет принужденного режима.

Для исследуемой цепи после окончания переходного процесса:

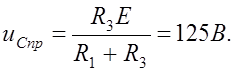
  (1)

3. Составление дифференциального уравнения.

Исходная система уравнений для момента времени после коммутации содержит 3 уравнения, записанные по законам Кирхгофа, и одно уравнение связи:

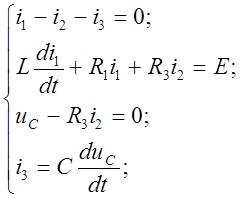(2)

(3)

(4)

(5)

Будем составлять дифференциальное уравнение относительно напряжения u_c.

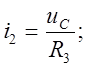Из (4):

(6)

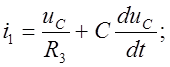Подставим (5) и (6) в (2):

(7)

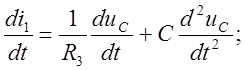Продифференцируем (7):

(8)

Подставим (6), (7) и (8) в (2):

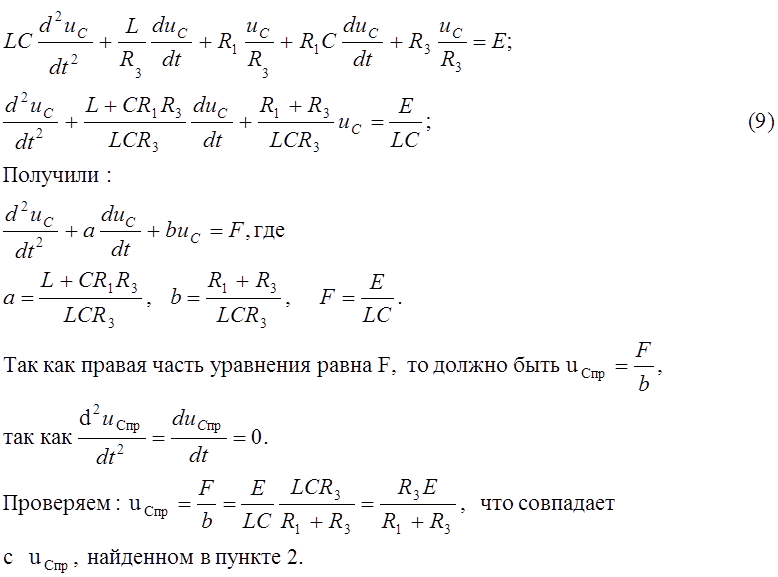
Проверка размерности:

4. Решение дифференциального уравнения.

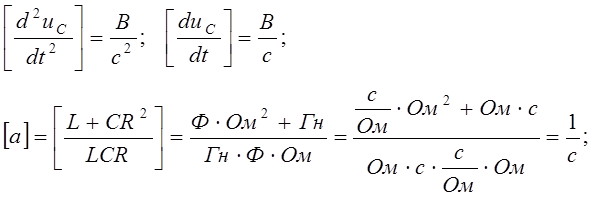
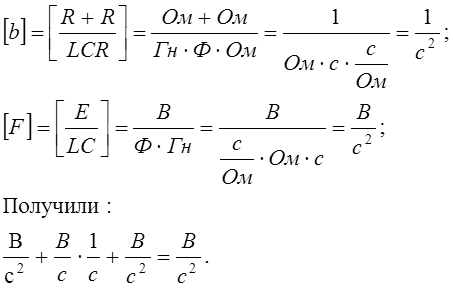
Характеристическое уравнение имеет вид:

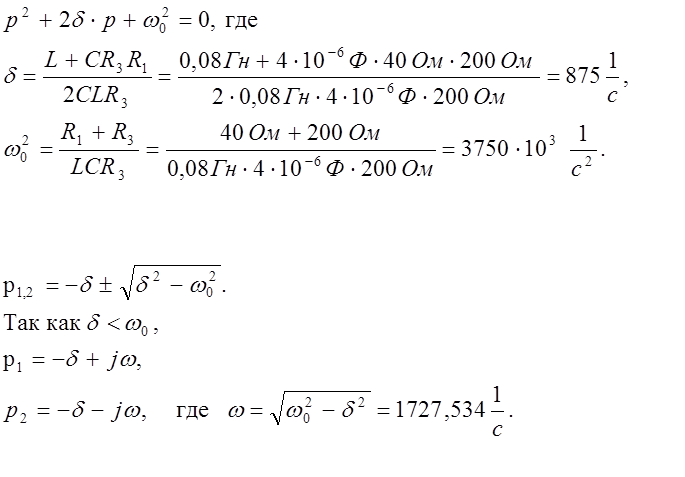
Корни характеристического уравнения:

следовательно корни комплексно сопряженные:         

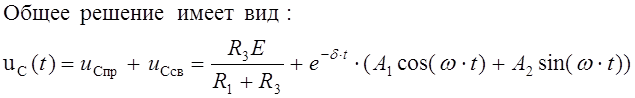
(10)

Определим независимые начальные условия. Для этого найдем ток в индуктивности и напряжение на емкости до коммутации:

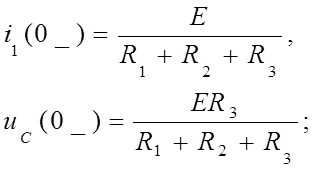
По законам коммутации определяем состояние катушки индуктивности и емкости в первое мгновение после начала переходного процесса:

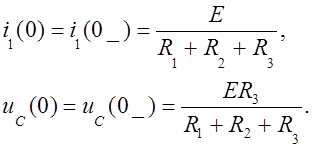
(11)

(12)

Для определения постоянных интегрирования А₁ и А₂ необходимо знать значение производной  в момент коммутации, т.е. при t=0. Для этого разрешим (7) относительно :

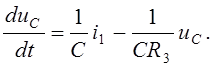                                                                                          (13)

Запишем (13) в момент коммутации:

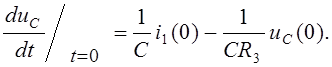
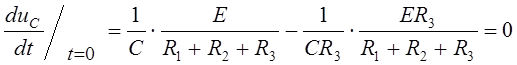Учитывая (11) и (12), получим:

                                 (14)

Дифференцируя (10), получим:

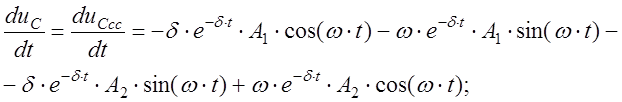
  (15)

При t=0 из (10) и  (15):

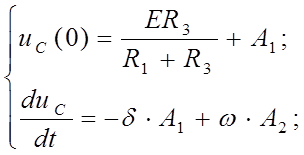
Используя (12) и (14) имеем:

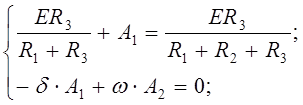
(16)

(17)

Из (16):

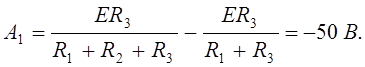
Из (17):

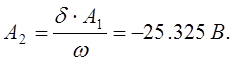
Подставляя А₁  и А₂  в (10), получим:

(18)

Проверка размерности:

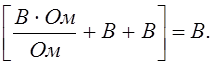
Делаем проверку при t=0: 

Из (18):        u_C(0)=125+(-50)=75.

Из (12):        u_C(0)=75.

Делаем проверку при t=: 

Из (18):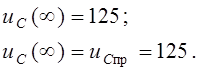       

Из (1):       

5. Определение остальных токов и напряжений в электрической цепи.

Из (6):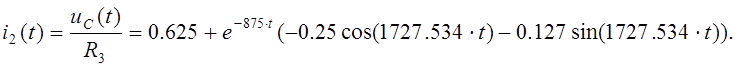

Из (5):

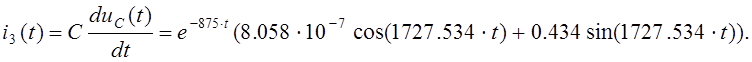
Из (2):

6. Операторный метод расчета электрической цепи.

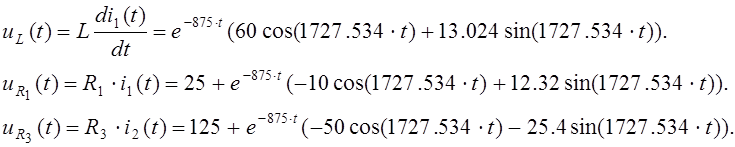
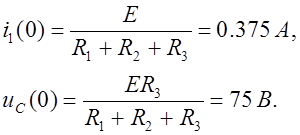Определим независимые начальные условия:

Схема замещения приведена на рис. 2.

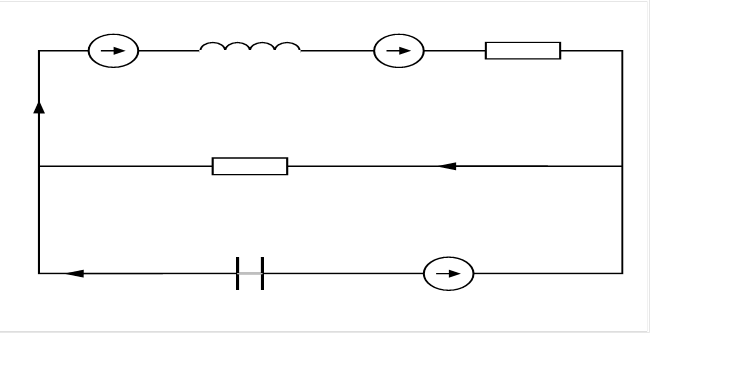
Рис. 2. Операторная схема замещения.

Составим систему уравнений по Законам Кирхгофа в операторной форме:

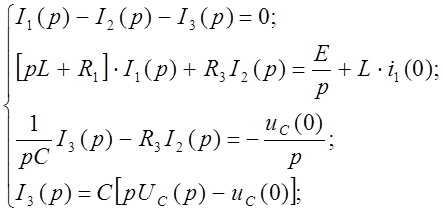(19)

(20)

(21)

(22)

Из (22):

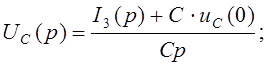                                                                              (23)

Из (21):

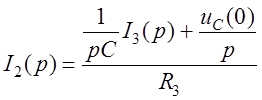
(24)

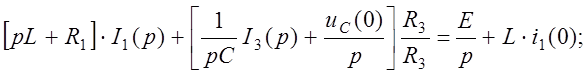Подставим (24) в (20):

                (25)

Разрешим относительно I₁(p):

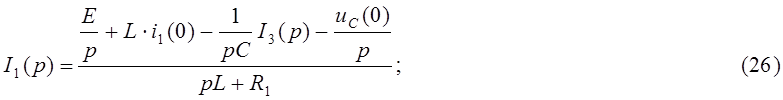
Подставим (24) и (26) в (19):

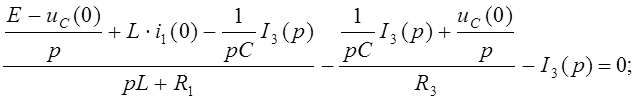
Разрешим относительно I₃(p):

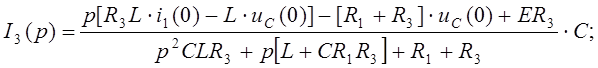
Подставляем в (22):

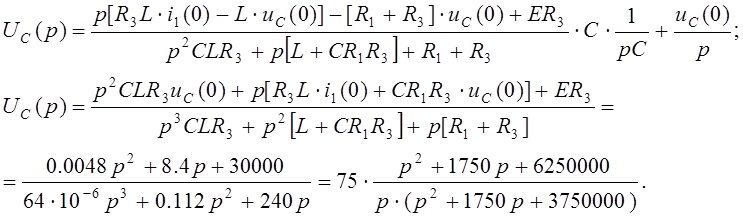
Разложив на простейшие дроби, получим:

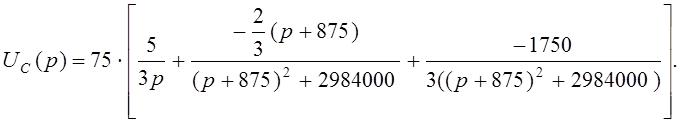
Найдем оригинал по данному изображению:

7. Сравнение результатов.

Напряжение на конденсаторе u_C(t), найденное классическим методом совпадает с напряжением, полученным операторным методом.

8. Графики токов и напряжений.

Графики изменения токов i₁(t), i₂(t) и i₃(t) приведены на рис. 3.

Рис.3. Графики изменения токов.

Проверка токов по 1 Закону Кирхгофа:

i₁(0.001) – i₂(0.001) – i₃(0.001) = 0.768 - 0.589 - 0.179 = 0,

i₁(0.003) – i₂(0.003) – i₃(0.003) = 0.597 - 0.625 – (-0.028) = 0.

Графики изменения напряжений  приведены на рис. 4.

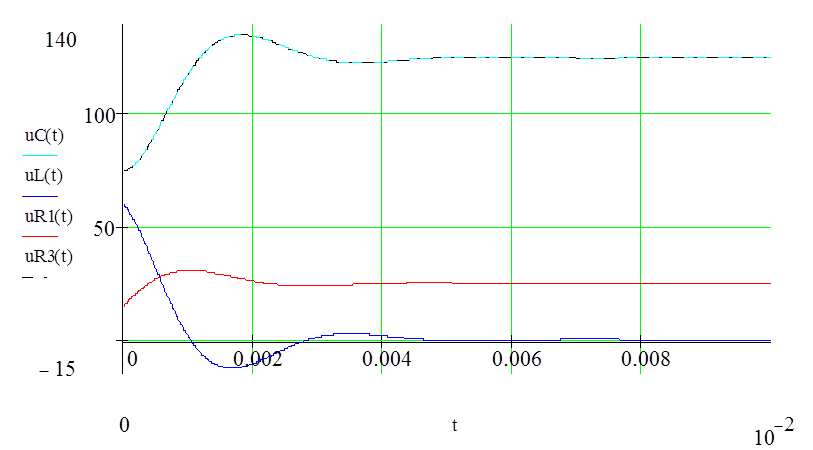Рис.4. Графики изменения напряжений.

Проверка напряжений по 2 Закону Кирхгофа:

9. Заключение.

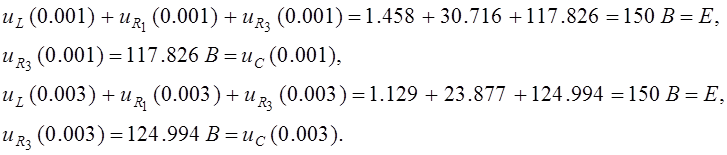
В ходе выполнения работы расчеты производились 2 методами (классическим и операторным), которые дали одинаковые результаты:

10. Список использованной литературы.

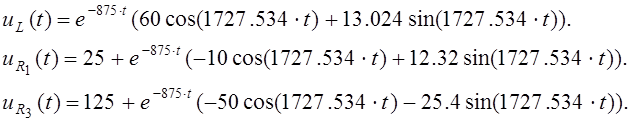
1.  Методические указания к домашним заданиям по расчету электрических цепей, под редакцией А.П.Лысенко.- Л.: ЛМИ, 1984.

2.  Конспект лекций.