



















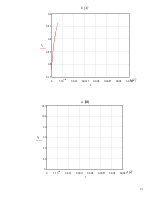


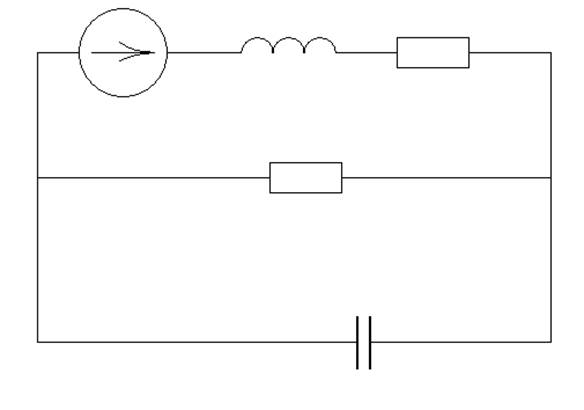
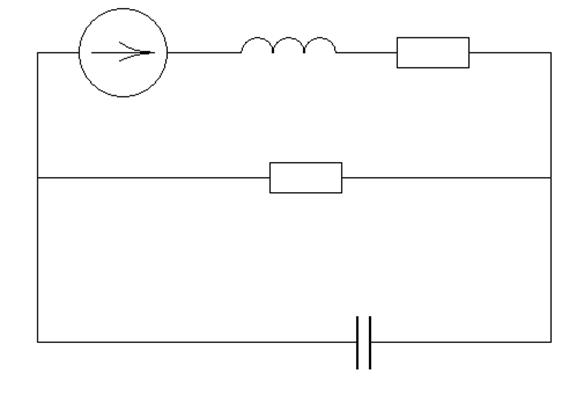
В цепи, изображенной на рисунке 1, происходит коммутация в момент времени t=0 (ключ Р замыкается). ЭДС источника Е=const.
E=170 В
L=0.1 Гн
C=6 мкФ
R1=350 Ом
R2=600 Ом
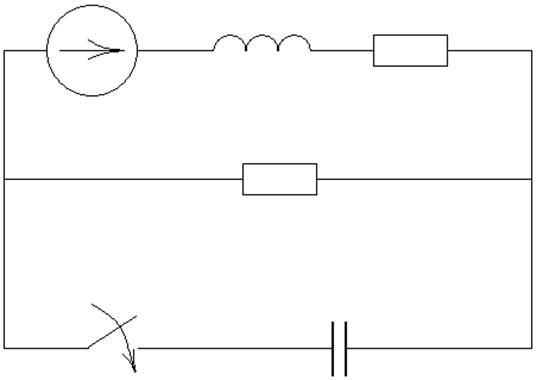
Рисунок 1
Требуется:
1. Найти законы изменения токов и напряжений на емкости и индуктивности. Задачу решить классическим и операторным методами.
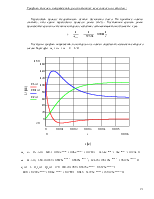
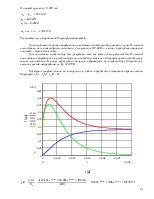
2. Построить временные диаграммы токов и напряжений.
3. Составить математическую модель переходного процесса по методу переменных состояния и подготовить систему дифференциальных уравнений. Полученные уравнения решить с помощью прикладных программ на компьютере.
4. Сравнить результаты расчета, полученные различными методами.
Будем рассматривать формулу входного сопротивления относительно ветви с источником.
Сопротивления R2 и ![]() соединены параллельно:
соединены параллельно:
Z =![]()
![]()
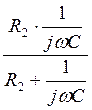 (1)
(1)
Входное сопротивление с учетом (1) имеет вид:
Zвх(jω) = jωL+R1+![]()
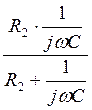 (2)
(2)
Zвх(![]() )=
)=![]() L+R1+
L+R1+![]()
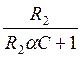 (3)
(3)
Затем прировняем данное уравнение (3) к нулю, преобразуем и найдем его корни:
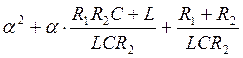 = 0 (4)
= 0 (4)
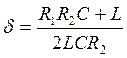 =
=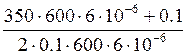 =1888.89 1/с (5)
=1888.89 1/с (5)
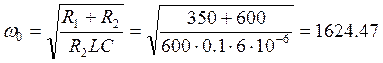 1/с
(6)
1/с
(6)
Преобразуем уравнение (4)
![]() (7)
(7)
Решим уравнение (7):
![]() 1/с
1/с
![]()
![]() 1/с
1/с
![]() Установившийся режим цепи
обусловлен действием источников энергии, и поэтому принужденная составляющая uc, в случае постоянного напряжения может быть
найдена методами расчета установившегося процесса в цепи после коммутации.
Установившийся режим цепи
обусловлен действием источников энергии, и поэтому принужденная составляющая uc, в случае постоянного напряжения может быть
найдена методами расчета установившегося процесса в цепи после коммутации.
В схеме разорвем ветвь с емкостью, так как при постоянном напряжении ток в цепи с конденсатором равен нулю:
ic(t)=![]()
ic(t)=0
По второму закону Кирхгофа, напряжение на конденсаторе после коммутации будет равно напряжению на резисторе R2:
uc=R2iL (8)
Так как ток через конденсатор равен нулю, то ток через резистор R2:
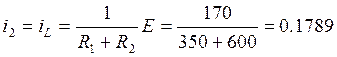 А (9)
А (9)
uc=R2iL=![]() В (10)
В (10)
4.1 Независимые начальные условия
Под начальными независимыми условиями понимают значения токов катушек индуктивности и напряжений на конденсаторе до коммутации.
По второму закону коммутации: uc(0-)=uc(0+). До коммутации ключ в ветви с конденсатором был разомкнут, значит uc(0-)=0.
Итак,
uc(0-)=uc(0+)=0 В (11)
По первому закону коммутации: iL(0-)=iL(0+)
До коммутации ток в катушке равен:
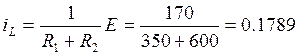 А (12)
А (12)
4.2 Зависимые начальные условия
Значения остальных токов и напряжений при t=0 в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа, называются зависимыми начальными условиями. Составим систему уравнений для определения зависимых начальных условий:
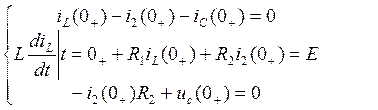 (13)
(13)
iC(0+)=C![]()
Подставим в систему независимые начальные условия:
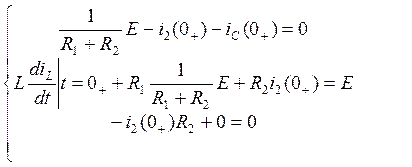 (14)
(14)
Преобразовав, получим:
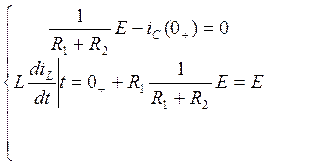 (15)
(15)
iC(0+)=C![]()
Из системы уравнений:
i2=0 А (16)
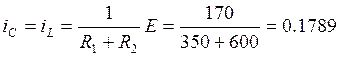 А (17)
А (17)
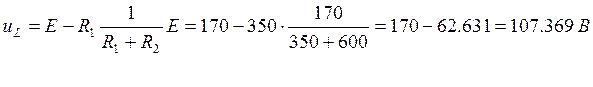 (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
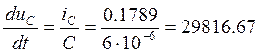 (21)
(21)
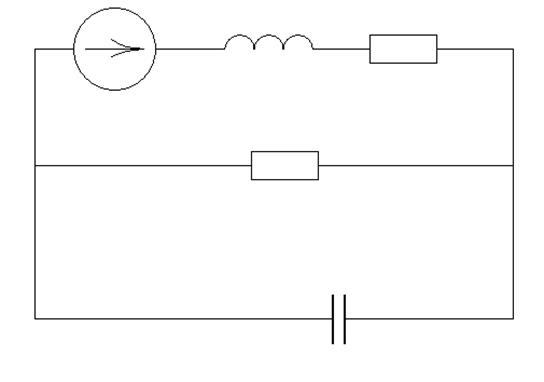
Вначале выберем условно-положительное направление токов в ветвях и направления обхода контуров. Затем запишем систему уравнений для момента времени после коммутации. Количество уравнений в системе должно быть равно числу неизвестных токов. Первое уравнение составим по первому закону Кирхгофа, второе и третье – по второму:
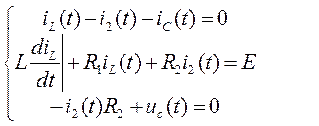 (22)
(22)
(23)
(24)
Уравнение связи для конденсатора:
iC(t)=C![]() (25)
(25)
Полученная система уравнений сводится к одному дифференциальному уравнению второго порядка относительно напряжения uC.
Для того чтобы выразить из системы uC, нужно исключить токи iL, iC, i2.
Из уравнения (24): 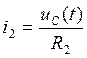 (26)
(26)
Уравнения (25) и (26) подставим в (22):
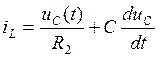 (27)
(27)
Уравнения (26) и (27) подставим в (23) и, преобразовав, получим:
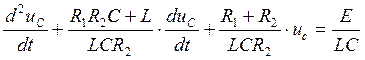 (28)
(28)
1. Проверка размерностей коэффициентов А и В.
А=1/с
В=1/с2
[Гн]= ![]()
[Ф]=с/Ом
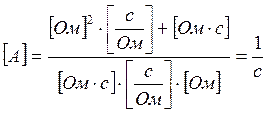
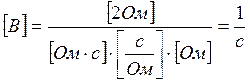
2. Проверка правой части.
При постоянном воздействии в установившемся режиме:
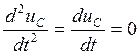
тогда uC
уст 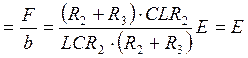
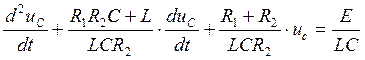
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.