Расчет переходных процессов (E=170 В, L=0,1 Гн, R1=350 Ом, R2=600 Ом, С=6 мкФ, ключ замыкается), страница 2

        —  линейное неоднородное дифференциальное  уравнение второго порядка. Известно, что решением таких уравнений является сумма двух составляющих, а именно, общего решения для соответствующего однородного уравнения и частного, полученного в форме правой части для неоднородного уравнения. Физический смысл первой составляющей – описание поведения системы при отсутствии внешнего воздействия. Эту составляющую принято называть свободной. Физический смысл второй составляющей – описание поведения системы при наличии внешнего воздействия, описываемого правой частью неоднородного уравнения. Эту составляющую принято называть принужденной. По существу, это описание нового установившегося процесса, в который должна будет перейти система после коммутации.

Таким образом, решение уравнения (28) запишется как .

Принужденная составляющая напряжения u_C определяется в установившемся режиме после коммутации и равна .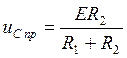

       Свободная составляющая u_{C св} определяется решением однородного дифференциального уравнения:

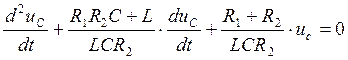,         (29)

позволяющем найти свободную составляющую напряжения , где А₁ и А₂ – постоянные интегрирования – определяются из начальных условий, а определяются как корни характеристического уравнения, соответствующего дифференциальному уравнению.

Определение постоянных интегрирования А₁ и А₂

Первое начальное условие:u_c(0_-)=u_c(0₊)=0 В

В момент времени t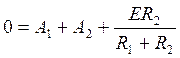=0:                 (30)

С учетом (30) получим выражение для u_C:

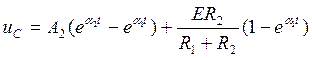           (31)

  

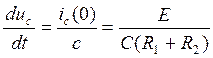
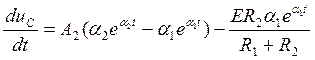    (32)

Запишем выражение (32) для момента времени t=0:

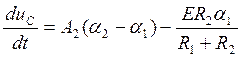    (33)

С учетом (21) получим:

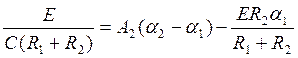  (34)

Преобразовав (34), получим:

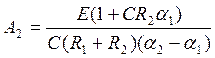                                         (35)

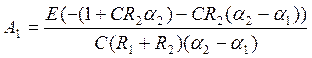                        (36)

Подставим (35) и (36) в решение и получим:

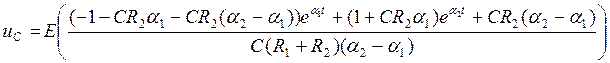           (37)

Проверка:

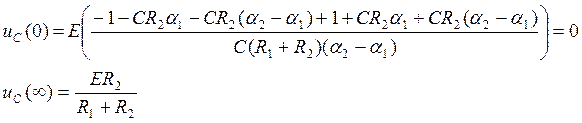
Подставим в решение численные значения корней и постоянные интегрирования определенные выше:

8.  Определение остальных токов и напряжений

Второй ток найдем из уравнения, составленного по второму закону Кирхгофа:

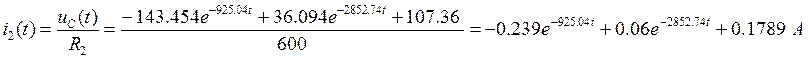
Из уравнения связи найдем ток через конденсатор:

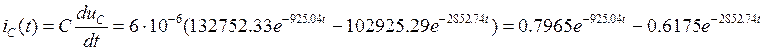A

Первый ток найдем из уравнения, составленного по первому закону Кирхгофа:

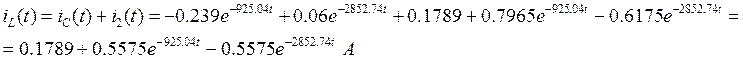
Напряжение на катушке индуктивности:

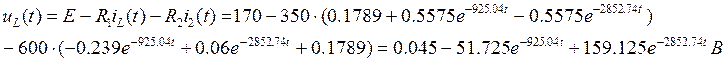
Падение напряжения на R₁:

Падение напряжения на R₂:

9.  Таблица проверок

Величина	Уравнение	t<0	t=0
			По закону Кирхгофа	По уравнению	По закону Кирхгофа	По уравнению
iL		0.1789	0.1789	0.1789	0.1789	0.1789
i2		0.1789	0	0.0001	0.1789	0.1789
iC		0	0.1789	0.179	0	0
uC(t)		0	0	0	107.36	107.34
uL(t)		0	107.369	107.445	0.045	0.045
uR1(t)		62.615	62.615	62.615	62.615	62.615
uR2(t)		107.34	0	-0.06	107.34	107.34

10.  Расчет переходных процессов методом переменных состояния

В основу метода переменных состояния положена принципиальная возможность замены дифференциального уравнения n-го порядка электрической цепи системой из n дифференциальных уравнений первого порядка. При этом в качестве переменных состояния принимают токи в индуктивности i_L и напряжение  u_C на емкостях, которые однозначно определяют запас энергии в любой момент времени. Переходный процесс в рассматриваемой цепи описывается системой дифференциальных уравнений в форме Коши и системой начальных условий.

Запишем систему, составленную по законам Кирхгофа:

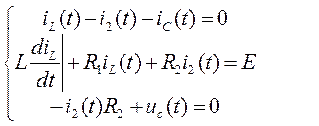
i_C(t)=C

Преобразуем полученную систему в систему уравнений в форме Коши относительно производных состояния:

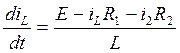
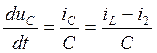
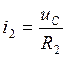
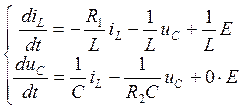
Полученная система является системой уравнений в форме Коши. Из этой системы запишем матрицу коэффициентов стоящих перед i_L и u_C:

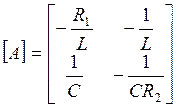  - эта матрица содержит все пассивные элементы цепи

Затем запишем матрицу коэффициентов стоящих перед входными воздействиями, то есть при Е:

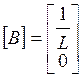
Так же объедим в систему  полученные раннее ННУ:

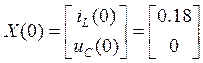 - матрица-столбец начальных условий

Запишем матрицу-столбец входных воздействий:

В итоге получим:

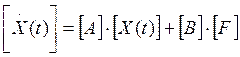, где Х(t) – матрица искомых величин.

Решение этой системы относительно Х имеет вид:

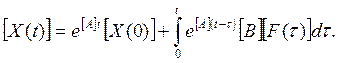
Первое слагаемое в этой формуле описывает свободные процессы в системе, а второе – принужденные при нулевом исходном состоянии.

        Матричную функцию е^[A]t вычисляют по формуле:

,  где

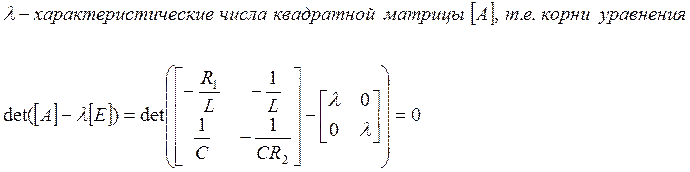
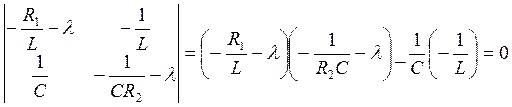
Преобразовав, получим характеристическое уравнение:

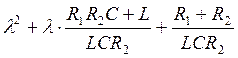=0

оно имеет корни

11.  Операторный метод расчета.

При использовании операторного метода действительные функции времени, называемые оригиналами, заменяют их операторными изображениями. Соответствие между оригиналом и изображением устанавливается с помощью некоторого функционального преобразования. Это преобразование выбирается так, чтобы операции дифференцирования и интегрирования оригиналов заменялись алгебраическими операциями над их изображениями. В таком случае дифференциальные уравнения для оригиналов переходят в алгебраические уравнения для их изображений.