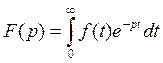
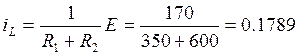 А
АuC(0)=0
При ненулевых начальных условиях в схему для изображений последовательно с индуктивностью включается дополнительный источник ЭДС, совпадающий с положительным направлением тока, а последовательно с емкостью – дополнительный источник ЭДС, противоположно направленный с положительным направлением тока в ветви.
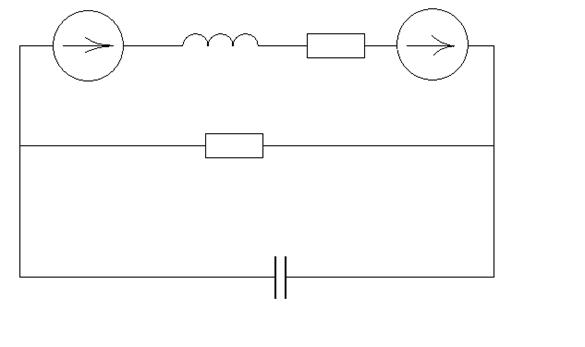
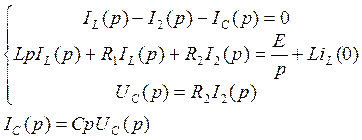
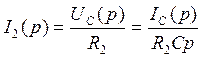
Затем выразим IL(p):
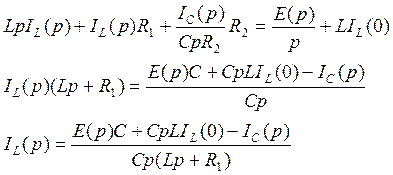
Затем найдем IC(p):
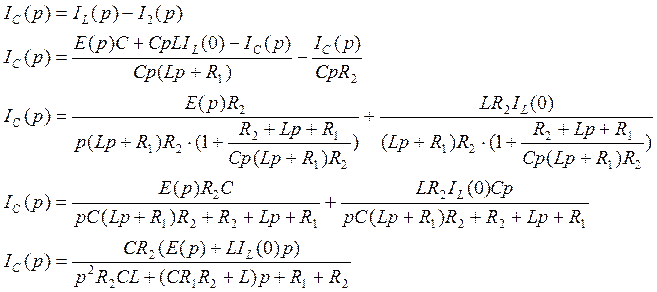
Найдем изображение UC(p):
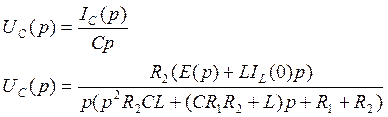
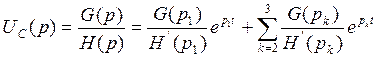
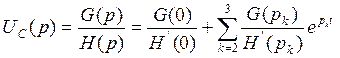
H’(p) – это производная знаменателя
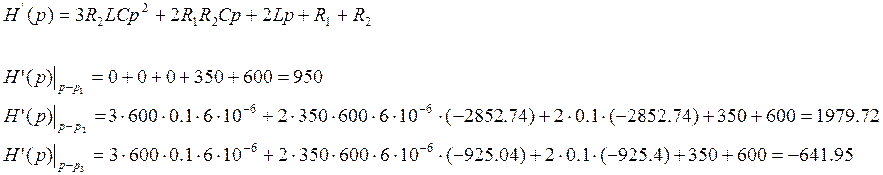
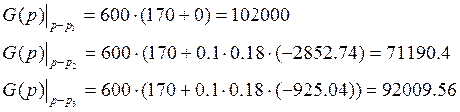
![]()
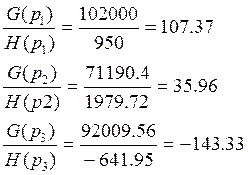
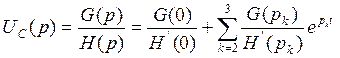 ,
получим
,
получимГрафики тока и напряжения, рассчитанные методом переменных состояния с помощью программы MathCAD.
Решение с применением метода Рунге-Кутта.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- квадратная матрица собственных коэффициентов системы, которые определяются структурой цепи и параметрами элементов;
- вектор независимых переменных, элементы которого определяются входными воздействиями;
- вектор начальных условий;
- D описывает правую часть уравнений, разрешенных относительно первых производных;
- начальный момент переходного процесса
- конечный момент переходного процесса
- число шагов для численных расчетов
Применение метода Рунге-Кутта. Решение Z
представляет собой матрицу размера N![]() . Первый столбец Z0 содержит моменты времени, столбец Z1 – значения тока iL, Z2 -значения функции uC, соответствующие этим моментам.
. Первый столбец Z0 содержит моменты времени, столбец Z1 – значения тока iL, Z2 -значения функции uC, соответствующие этим моментам.
|
|
IL [A]
|
|
t [c]
t [c]
Графики токов и напряжений, рассчитанных классическим методом:
Переходный
процесс теоретически длится бесконечно долго. На практике можно считать, что
время переходного процесса равно (3-4)![]() .
Постоянная времени равна промежутку времени, в течение которого свободная
составляющая тока убывает в e раз.
.
Постоянная времени равна промежутку времени, в течение которого свободная
составляющая тока убывает в e раз.
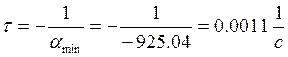
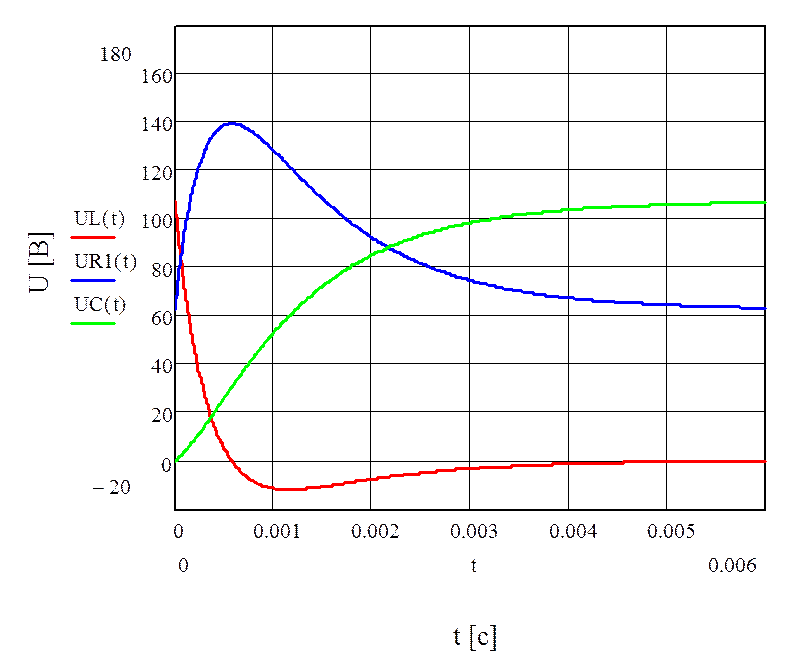
Построим
графики напряжений, по которым мы можем определить выполнение второго закона
Кирхгофа: ![]()
![]()
![]()
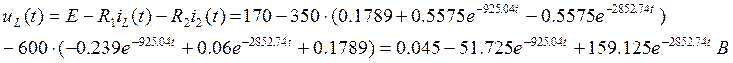
В момент времени t=0.005 сек:
![]() 105.954 B
105.954 B
![]() = 64.527B
= 64.527B
![]() = -0.462B
= -0.462B
![]() 170.019B
170.019B
Следовательно, второй закон Кирхгофа выполняется.
До коммутации падение напряжения на катушке индуктивности равнялось нулю. В момент коммутации оно скачкообразно изменилось до величины 107.44 В и к концу переходного процесса оно опять стремится к нулю.
До коммутации конденсатор был разряжен, так как ветвь была разомкнута. В момент коммутации напряжение на конденсаторе не изменяется, так как это противоречило бы второму закону коммутации. К концу переходного процесса напряжение на конденсаторе стремится к величине равной напряжению на R2, 62.615 В.
Построим графики токов, по которым мы можем определить выполнение
первого закона Кирхгофа: ![]()
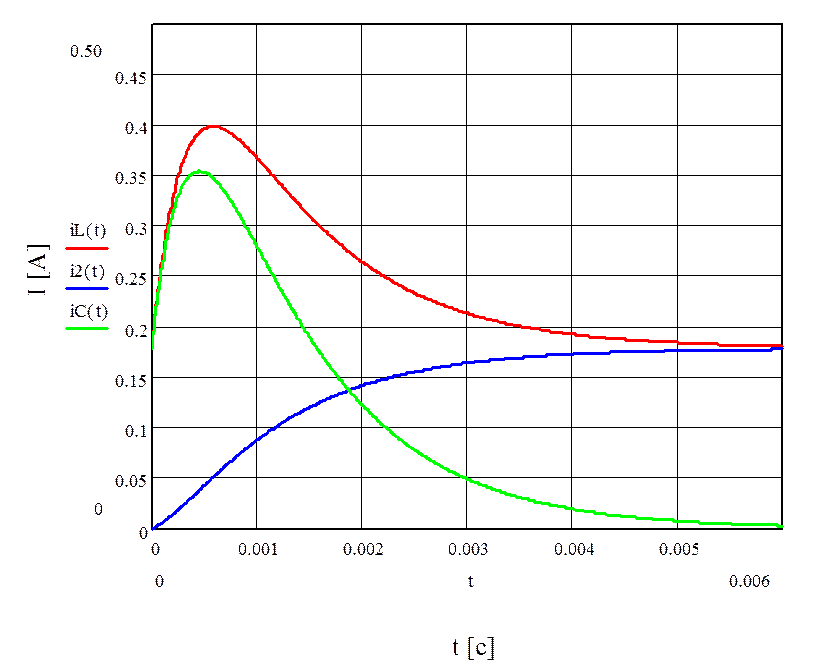
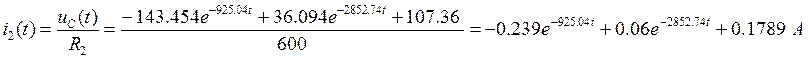
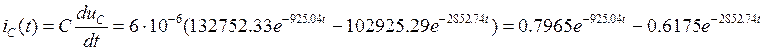 А
А
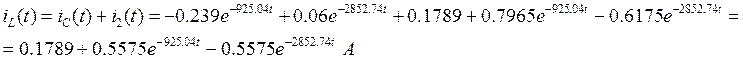
В момент времени t=0.005 сек
i2(t)= 0.177 A
iC(t)= 0.0078 A
iL(t)= 0.184 A
![]()
Следовательно, первый закон Кирхгофа выполняется.
Сравним графики, полученные при ручном расчете классическим методом и машинным расчетом с применением метода Рунге-Кутта.
На графиках максимум IL лежит в диапазоне от 0.0005 до 0.001 сек.
При t=0.002c значение il на обоих
графиках совпадает и равно 0.0265A, при t=0.004c, iL=0.193A, а при ![]() , iL=0.18A
, iL=0.18A
Графики uC возрастают от 0 до величины равной 107В, при этом, при t=0.002c, uC=84.8B, а при t=0.004c, uC=103.4B.
Таким образом, решая поставленную задачу различными способами, мы получили один и тот же результат.
1. Электротехника. Домашние и курсовые задания. Под редакцией П.А. Галайдина.
2. Теоретические основы электротехники. Л.Р. Нейман, К.С. Демирчян.
3. Теоретические основы электротехники. Электрические цепи. Л.А. Бессонов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.