





Лабораторная работа №2
Численное решение уравнения масс
летательного аппарата (ЛА).
> restart;
Digits := 5;
![]()
Методические указания.
Цель и содержание работы.
Цель - ознакомление с итерационными методами решения уравнений на примере решения уравнения масс ЛА методом последовательных приближений.
Содержание работы:
Рассматривается задача определения стартовой массы ЛА m0 в зависимости от проектных переменных. Подобные задачи решаются на этапе баллистического проектирования ЛА.
Основным путем повышения точности расчета ![]() является т.н. путь
декомпозиции массы, согласно которому
является т.н. путь
декомпозиции массы, согласно которому ![]() представляет собой сумму масс соотвествующих структурно -
функциональных элементов ЛА
представляет собой сумму масс соотвествующих структурно -
функциональных элементов ЛА ![]() .
.
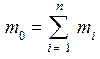 .
.
В лабораторной работе приняты следующие обозначения:
f - уравнение масс летательного аппарата;
m_p - масса полезной нагрузки;
m_pl - масса конструкции планера ЛА;
m_jet - масса двигательной установки;
m_fuel - масса топлива;
m_0 - стартовая масса ЛА;
Остальные обозначения вводятся по мере необходимости.
Порядок выполнения лабораторной работы:
- присвоить переменным m_p, k_pl,alpha иmu значения в соответствии с полученным заданием;
- задать точность расчета для решения уравнения масс epsilon (0,01 ... 0,0001);
- произвести расчеты путем выбора пункта Edit \ Execute \ Worksheet главного меню среды Maple 6.
В ходе лабораторной работы требуется исследовать:
- условия сходимости метода последовательны итераций;
- зависимость числа итераций, требующихся для обеспечения заданной точности расчетов, от значений точности;
- влияние числа значащих цифр, определяемого константой Digits на относительную погрешность расчетов delta при одинаковой точности расчетов epsilon.
Уравнение масс.
> f := m_p + m_pl + m_jet + m_fuel;
![]()
> m_pl := k_pl*m0;
m_jet := alpha*mu*m0;
m_fuel := mu*m0;
![]()
![]()
![]()
> f;
![]()
> collect(f,m0);
![]()
Исходные данные.
Масса полезной нагрузки m_p.
> m_p := 137;
![]()
Коэффициент (относительная масса) планера ЛА k_pl.
> k_pl := 0.33;
![]()
Коэффициент качества двигателя alpha.
> alpha := 0.4;
![]()
Относительная масса топлива mu.
> mu := 0.42;
![]()
Решение уравнения масс ЛА.
Численное решение уравнения масс.
Точность расчетов epsilon.
> epsilon := 0.0001;
![]()
Максимальное допустимое число итераций i_max.
> i_max := 100;
![]()
Первое (начальное) приближение:
> x[1] := 100;
![]()
Второе приближение:
> x[2] := eval(f,m0 = x[1]);
![]()
> for i from 3 while (abs((x[i-1] - x[i-2])
/x[i-2]) > epsilon
and i <= i_max) do
x[i] := eval(f, m0=x[i-1]):
end do;
if i <= i_max then
m0_approx := x[i-1]:
print(" Стартовая масса m0 = ",m0_approx):
print(" Число итераций ",i-1):
else
print(" Число итераций превысило допустимое"):
end if:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Точное решение уравнения масс.
> f;
![]()
> eqn := f = m0;
![]()
> m0 := solve(eqn,m0);
![]()
Сравнение результатов.
Относительная ошибка delta.
> delta := 2*abs(m0 - m0_approx)/(m0 + m0_approx);
![]()
>
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.