1. Поступательное движение а.т.т.
![]() =
= ![]() - скорость любой точки равна скорости
полюса, за полюс принимается центр инерции
- скорость любой точки равна скорости
полюса, за полюс принимается центр инерции
T = ½ ∫ Vc2dm = ½ mVc2 (37); (∫dm = m)
(m)
2. Тело вращается около (вокруг) неподвижной оси: l = Ox:
V = ωhx → в (36)
T = ½ ∫ hx2ω2dm = ½ ω2 ∫ hx2dm = ½ Ix ω2
(m) (m)
Ix = ∫ hx2dm - осевой момент инерции а.т.т.
(m)
T = ½ Ix ω2 (38)
3. Твёрдое тело вращается около (вокруг) неподвижного полюса.
 |
l


ω V = ωhω
![]()
hω T = ½ ∫ω2hω2dm = ½ ω2 ∫hω2dm (39)
![]()
![]()
![]()
![]()
![]()
![]()
![]() (m)
(m)
(m)
(m)
Iω = ∫hω2dm - момент инерции относительно мгновенной оси вращения
(m)
T = ½ Iωω2 (39)
4. Плоско-параллельное движение а.т.т.
T = ½mVc2 + Tr ; Tr = ½Icz’ω2
T = ½mVc2 + ½Icz’ω2 (40)

![]()
![]()

![]() Y Y’
Y Y’
 |
X’
rc C
O X
![]()

Z’
Z
5. Общий случай движения а.т.т.
По теореме Кёнига: T = ½ mVc2 + Tr
Tr – кин. энергия относительного движения тела (вращение а.т.т. вокруг точки С как вокруг неподвижного полюса).
Tr = ½ Iωω2 (см. 39’)
T = ½ mVc2 + ½ Iωω2 (41)
Момент инерции абсолютно твёрдого тела.
Определение: Моментом инерции твёрдого тела относительно оси называется скалярная существенно положительная величина, являющаяся мерой инерции этого тела при вращении вокруг (около) указанной оси.
T =½ IeW2
Ie = ∫he2dm
(m)
Ix, Iy, Iz совокупность 3-х осевых и 3-х центробежных
Ixy = Iyx ; Iyz = Izy ; Izx = Ixz моментов инерции
Характеризует распределение массы в абсолютно твёрдом теле при его вращении около оси.
Ix -Ixy -Ixz − тензор инерции
-Ixy Iy -Iyz
-Ixz Izy Iz
Момент инерции твёрдого тела относительно осей главной (непод. сист. коорд.) (см. выше)
Ix = ∫(y2+z2)dm = ∫hx2dm
(m) (m)
Iy = ∫(x2+z2)dm = ∫hx2dm
(m) (m)
Iz = ∫(x2+y2)dm = ∫hz2dm
(m) (m)
I0 = ∫(x2+y2+z2)dm − полярный момент инерции
(m)
Момент инерции плоского тела, у которого один размер мал по сравнению с двумя другими тв. тело gпринадлежит пл. xoy: z = 0
Ix = y2dm Iz = ∫(x2+y2)dm
(m)
Iy = x2dm I0 = ∫(x2+y2)dm
(m)
Iz = I0 = Ix+ Iy − (42) для плоского тела, принадлежащего плос. XOY
Частные случаи:
1. Моменты инерции однородной материальной (вещественной) окружности («кольца»)
Дано: m, R
Опр: Ix, Iy, Iz, I0
![]() Y
Y
 |

dm
R
O X
 |
Z
Т.к. окружность − плоское тело, принадлежащее плос. xoy, то Iz = I0
Ix + Iy = I0
I0 = ∫R2dm = R2∫dm = mR2
(m) (m)
Iz = mR2
Ix = Iy = ½ I0 = ½ mR2 (43)
2. Момент инерции сплошного (однородного) диска (круга)
![]()
 Y
Y
 Дано: m, R
Дано: m, R
Опр: Ix, Iy, Iz, I0

 Iz
= I0; Ix = Iy = ½ I0 (см. (42))
Iz
= I0; Ix = Iy = ½ I0 (см. (42))

O r X
![]()

![]()
R
Z
Круг «разбиваем» не б. б. число б. малых элементов концентрическими окружностями
I0 = 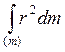 ; dm =
; dm =![]() 2πr·dr
2πr·dr
I0 = ![]()
![]() 2πr·dr
=
2πr·dr
= ![]()
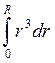 =
= ![]()
![]() = ½mR2
= ½mR2
![]()
Iz = I0 = ½mR2
(44)
Ix = Iy = ¼mR2
3. Момент инерции однородного шара (сферы)
Дано: m, R
Опр: Ix, Iy, Iz, I0
Для шара:
Ix = Iy = Iz = 2/3 I0
2 I0 = Ix + Iy + Iz
I0 = ∫r2dm ; dm = m/ 4/3πR3 4πr2dr = 3m/R3 r2dr
(m)
R
I0 = 3m/R3 ∫r4dr = 3/5 mR2
0
Ix = Iy = Iz = 2/3 3/5 mR2 = 2/5 mR2 (45)

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.