Классификация сил по характеру производимой работы. Кинетическая энергия системы материальных точек, страница 2

(x_н,y_н,z_н)

П(x,y,z) = ∫ (K_xdx + K_ydy + K_zdz)

(x,y,z)

(x,y,z)

U(x.y.z) = ∫ (K_xdx + K_ydy + K_zdz)

(x_н,y_н,z_н)

П(x,y,z) = - U(x,y,z) … (31)

Уравнение кинетической энергии м.т. в частном случае, когда вещественная т. находится под действием только консервативных сил (закон сохранения механической энергии).

V0                          M                    V

                                                                                                                  T – T₀ = A   (°)

A = U – U₀  (см.°)                   

M0         

U(x,y,z) – значение                      

потенциальной функции в т. М

U₀(x₀,y₀,z₀) – значение    потенциальной функции в т. М₀  

T – T₀ = U – U₀

U = -П

U₀ = -П₀

T – T₀ = -П + П₀

 

T + П = T₀ + П₀

T + П = Е                    Е – Е₀  (32)

T₀ + П₀ = Е₀

При движении м.т. в данном динамическом поле сумма кинетической и потенциальной энергий точки постоянна и равна значению в начале движения (закон сохранения полной мех. Энергии точки).

3 б.   Кинетическая энергия системы м. точек

Begin 2 (см. °)

Опр: Кинетической энергией системы вещественных точек в некоторый момент времени t  называется скалярная, существенно положительная физическая величина, характеризующая динамическое состояние системы в данный момент времени t, равная системе кинетических энергий всех точек системы.

T = = ½ V_j²  … (33)

Теорема об изменении кинетической энергии с.м.т.

(m₁, m₂,… m_n),   {, ,… } 

(m₁, m₂,… m_n).

За [0, t] скорости j-ой точки изменяются от  до

Теорема об изменении кинетической энергии для j-ой точки:

½m_jV_j² - ½m_jV_j0² = A_j     Aj – работа всех сил, приложенных к j-ой точке при перемещении точки       M_j0 в положение M_j

A_j = A_j^e + A_jⁱ

½m_jV_j² - ½m_jV_j0² = A_j^e + A_jⁱ … (j = 1, 2,… n)

Просуммируем n раз:

½V_j² - ½V_j0² =  +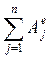

 

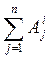
T                  T₀                 A^e           Aⁱ

T - T₀ = A^e + Aⁱ … (34) – матем. Запись теоремы об изменении кин. энергии с.м.т.

Теорема: Изменение кин. энергии с.м.т. = сумме работ всех внешних и всех внутренних сил, действующих на данную систему при её перемещении относительно выбранной с.о.

Для неизменяемой системы Aⁱ = 0 на любом перемещении.      

T - T₀ = A^e    (34)*    для неизменяемой с.м.т.

Опр: Неизменяемой называется такая с.м.т., в которой расстояние между точками системы остаётся неизменным при перемещении всей системы.

Теорема Кёнига – устанавливает связь кин. энергию системы с т.С – центром инерции системы.

                         Y                            Y’

                                                                            M_j

r_j                  ρ_j

X’

C

r_c                                                             X    

O                                               

Z’

Z

Движение с.м.т. относительно выбранной с.о. будем рассматривать как сложное движение, состоящее из наложенных один на другое одновременных действий: движения относительно осей промежуточной с.к. и движения, обусловленного перемещением промежуточной с.к. относительно неподвижной с.к. Oxyz.

Тогда любая точка системы будет находиться сложном движении, т.е. двигаться относительно двух с.о.

Н.с.к. Oxyz – 2-ая с.о. (абсолютная):  = – скорость абсолютного движения j-ой точки

Промежуточная с.к. Сx’y’z’ − 1-ая с.о. (подвижная)

 =

Переносное движение неизменяемой среды, неизменно связанной с 1-ой с.о. относительно 2-ой с.о., т.е. движение Сx’y’z’ относительно Oxyz.

 =  − скорость движения центра инерции системы.

 =  =  +

Кин. энергия системы   T = ½ V_j² = ½  () = ½  ( + )( + ) =                         

= ½  () +  () + ½  ()

Рассмотрим отдельно слагаемые:

½  () = ½ V_jr²  = T_r  − кин. энергия с.м.т. в относительном движении

 () =  () =  =  =  0

    

m’ = 0

ρ_c’ = 1/m ρ_j = 0   (совпадает с началом координат промежуточной системы координат)

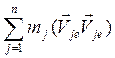½ = ½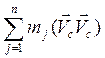= ½mV_c²

T = ½  (V_jeV_je) = ½  (V_cV_c) = ½ mV_c²  

T = ½ mV_c² + T_r  (35) , где   T_r = ½ V_jr² , m =

Теорема Кёнига: Кин. энергия с.м.т. равна сумме кин. энергий: кин. энергия м.т., имеющей массу данной системы  и совпадающей с центром инерции данной системы, и кин. энергии с.м.т. относительно осей координат, начало которых совпадает с центром инерции системы и параллельных осям данной промежуточной системы координат (кин. энергия относительного движения).

3 в.   Кинетическая энергия абсолютно твёрдого тела.

Для с.м.т. кин. энергия:  T = ½ V_j²

по теории Кёнига:  T = ½ mV_c² + T_r ,   T_r = ½ V_jr   

n

Для а.т.т.:      lim     ∑ ½ Δm_jV_j² = ½ ∫ V²dm   (36)  - справедлива для любого движущегося а.т.т.

Δm_j→0  j=1                     (m)

n→∞

Определение кин. энергии а.т.т. в различных случаях движения.