






![]()
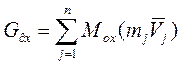 Кинетический момент систем материальных точек
Кинетический момент систем материальных точек
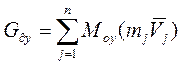 (12) относительно координатных осей
(12) относительно координатных осей
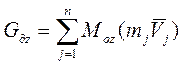
![]() Самостоятельно: из учебника:
( Доказательство в учебниках)
Самостоятельно: из учебника:
( Доказательство в учебниках)
![]() …..
(13)
…..
(13)
Связь между кинетическим моментом с.м.т. относительно неподвижного полюса «0» с моментом количества движения точки, имеющей массу всей системы и совпадающей с центром инерции системы.
2,б Теорема об изменении кинетического момента с.м.т. относительно неподвижного полюса.
См. begin 2 (m1, m2,…. mn)
(m1V1, m2V2, …. mnVn) j=1,2,….,n
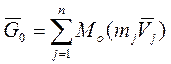 (постоянно с t’ величина и направление неизменно только в точке приложения
«0»)
(постоянно с t’ величина и направление неизменно только в точке приложения
«0»)
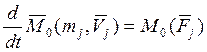 (j=1,2,….,n)
(j=1,2,….,n)
![]()
(равнодействующая всех сил приложенных к j-той точке системы)
![]() (j=1,2,3….n)
(j=1,2,3….n)
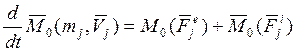 (j=1,2,….n)
(j=1,2,….n)
Просуммируем все части равенства от 1 до n. Все векторы имеют общую точку приложения т. «0»
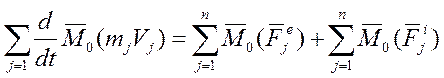 (**)
(**)
(1):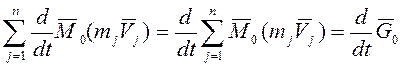
(2): 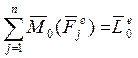 - главный момент всех
внешних сил, действующих на все точки с.м.т. относительно «0»
- главный момент всех
внешних сил, действующих на все точки с.м.т. относительно «0»![]()
(3): 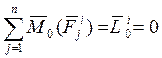 - гл.момент всех
внутренних сил т.к. главный вектор равен 0, то и
- гл.момент всех
внутренних сил т.к. главный вектор равен 0, то и
Главный момент равен = 0)
Тогда ![]() ,
, 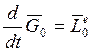 (14) математическая запись теоремы об
изменинии кинетического
(14) математическая запись теоремы об
изменинии кинетического
Момента с.м.т. относительно неподвижного полюса «0»
ТЕОРЕМА: Производная по времени от кинетического момента с.м.т. относительно
Неподвижного полюса «0» равна главному моменту всех внешних сил, действующих на данную систему относительно того же неподвижного полюса «0»
Спроектируем (14) на координатные оси, получим:
![]()
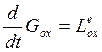
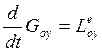 (15) Математическая
запись теоремы об изменении кинетического момента с.м.т. относительно
координатных осей
(15) Математическая
запись теоремы об изменении кинетического момента с.м.т. относительно
координатных осей
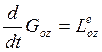
Частные случаи:
1) ![]() ;
; 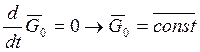 Закон сохранения кинетического момента
с.м.т. от неподвижного
полюса «0»
Закон сохранения кинетического момента
с.м.т. от неподвижного
полюса «0»
а) внешние силы отсутствуют!
в) главный момент внешних сил относительно точки O равен 0 (Пример: центробежная сила)
2) ![]() ;
; 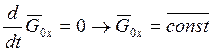 Закон сохранения кинетического момента
с.м.т относительно оси
Закон сохранения кинетического момента
с.м.т относительно оси ![]()
система сил ![]()
![]() ; но
; но ![]() ;
; 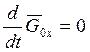 ;
; ![]() ;
; ![]()
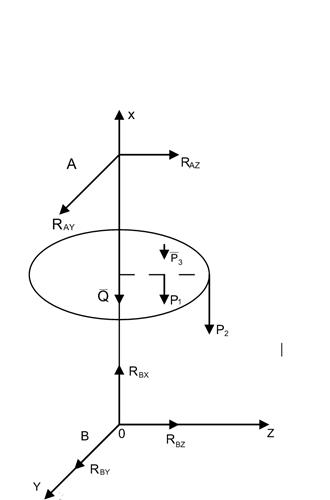
2.в. Кинетический момент а.т.т относительно неподвижного полюса.
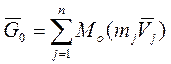 - для с.м.т. а. тв. тело
«разбиваем» на бесконечно большое число бесконечно малых элементов в момент времени t …..
- для с.м.т. а. тв. тело
«разбиваем» на бесконечно большое число бесконечно малых элементов в момент времени t ….. ![]()
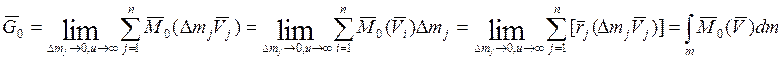
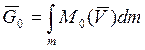 (15)
(15)
Частный случай : а. твердое тело вращается около неподвижного полюса «0»
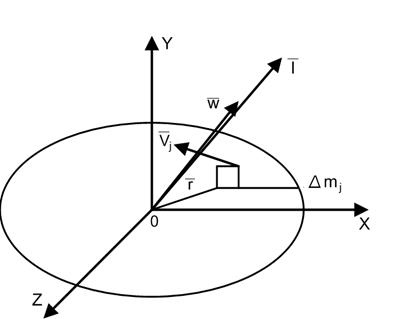
![]() ;
;
![]()
![]()
![]()
![]()
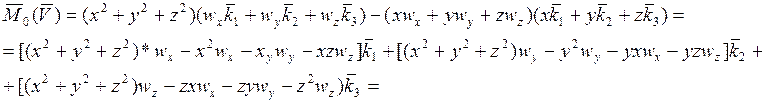
Сгруппировали слагаемые с одинаковыми ортами, привели
подобные члены, далее подставляем ![]() в равенство (15)
интеграл от суммы на сумму интегралов и группируем:
в равенство (15)
интеграл от суммы на сумму интегралов и группируем:
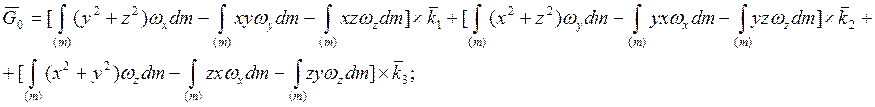
(выносим за знак интеграла составляющие угловой скорости) и обозначим:
![]()
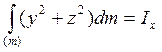
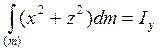 (16)
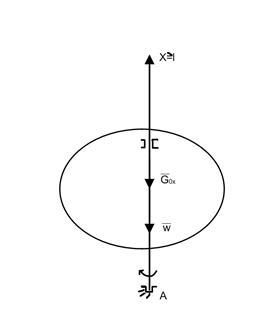
Осевые моменты инерции а.т.т
(16)
Осевые моменты инерции а.т.т
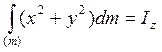
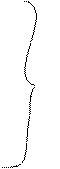
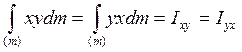
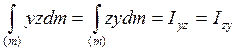 (17)
Центробежные моменты инерции а.т.т
(17)
Центробежные моменты инерции а.т.т
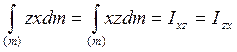
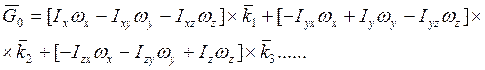 (18) Кинетические моменты
а.т.т.
(18) Кинетические моменты
а.т.т.
относительно неподвижного полюса «О» при вращении около точки «О».
Частный случай: Абсолютно твёрдое тело вращается около (вокруг) неподвижной оси.
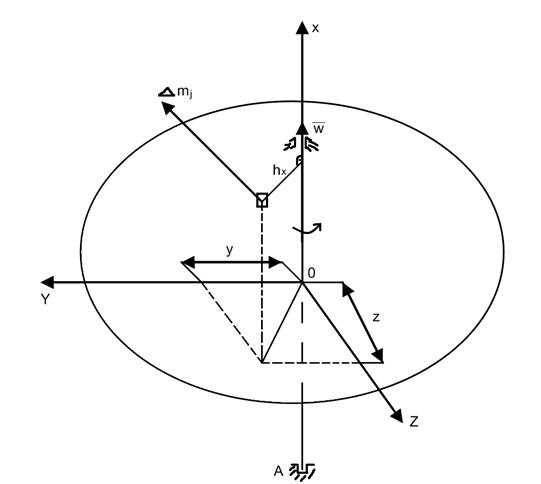
А.т.т вращается вокруг оси ![]()
![]() в (18)
в (18) ![]()
![]() )
)
(точка 0 ![]() оси
оси ![]() ) ,
) , ![]() (
(![]()
![]() (19)
(19)
![]() (*)
(*)
![]() (20) - Кинетический момент а.т.т относительно оси вращения
(20) - Кинетический момент а.т.т относительно оси вращения ![]() .
.
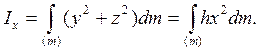
![]() элемент массы настолько мал, что
мы его рассматриваем как точку, тоже
элемент массы настолько мал, что
мы его рассматриваем как точку, тоже ![]() - диагональ
параллелограмма (см.(v))
- диагональ
параллелограмма (см.(v))
Из (20) ![]()
![]() , т.к.
, т.к. ![]() , то знак
проекции кинетического момента совпадает со знаком проекции угловой скорости
тела.
, то знак
проекции кинетического момента совпадает со знаком проекции угловой скорости
тела.
![]() , если
, если ![]() ,
то
,
то ![]()
если ![]() , то
, то ![]()
3,а. Третья динамическая характеристика м. т. ( и др.)- кинетическая энергия.
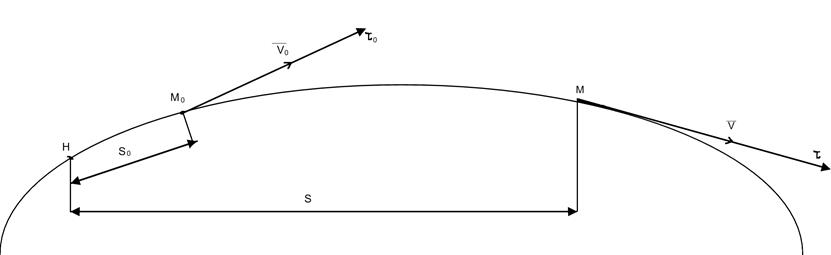
Пусть м. т. массы m
движется под действием системы сил ![]() относительно некоторой
с. о. При этом движение задаётся траекторной координатой
относительно некоторой
с. о. При этом движение задаётся траекторной координатой ![]() в начальный момент времени и далее она
переместилась в положение, определяемое траекторной координатой S.
в начальный момент времени и далее она
переместилась в положение, определяемое траекторной координатой S.
Определение: Кинетической энергией м.т. в данный момент времени t называется скалярная
существенно положительная физическая величина, характеризующая динамическое состояние м.т. в момент времени t, определяемая по формуле:
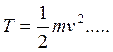 (21)
(21)
![]() (2-ое начало динамики),
спроектируем на касательную, получим:
(2-ое начало динамики),
спроектируем на касательную, получим:
![]() ;
; 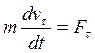
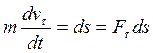
![]()
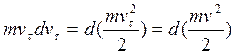
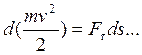 (22)- уравнение кинетической энергии м.т. в диффер.
форме!
(22)- уравнение кинетической энергии м.т. в диффер.
форме!
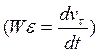
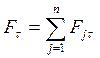
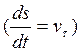
![]()
![]()
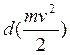 - элементарная
кинетическая энергия материальной точки
- элементарная
кинетическая энергия материальной точки
Обозначим: ![]() (23) –
Элементарная работа равнодействующей с. сил, действующая на материальную точку
(23) –
Элементарная работа равнодействующей с. сил, действующая на материальную точку
(22) –уравнение кинетической энергии точки в дифиренциальной форме.
![]() …. (22)’
…. (22)’
Равенство (22) проинтегрируем в указанных пределах:
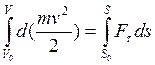
Обозначим: 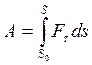 (24) –
работа равнодействующей системы сил приложенных и рассмотренной
материальной точки
(24) –
работа равнодействующей системы сил приложенных и рассмотренной
материальной точки
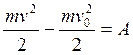 (25)
(25)
T-T0=A (25)’
(25) и (25)’ – математическая запись теоремы об изменении кинетической энергии точки – уравнение кинетической энергии материальной точки в интегральной форме.
Теорема: Изменение кинетической энергии материальной точки при ее перемещении из некоторого начального положения в данное равно работе равнодействующей всех сил, приложенных к данной точке на указанном перемещении [S0, S]
Формулы для определения работы силы.
Определение: Работой силы приложенной к материальной точке называется скалярная величина, характеризующая механическое действие силы на данном перемещении материальной точки
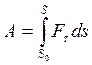 (24)
(24)
![]() (23)
(23)
Определение: Работа силы через алгебраические величины её проекций на оси декартовых
Координат
Пусть точка перемещается из М0 в М

![]() (*) расположение вектора
равнодействующей системы сил по базису декартовых
координат
(*) расположение вектора
равнодействующей системы сил по базису декартовых
координат
![]()
![]() , где
, где ![]() - орт.
касательной (скалярного произведения)
- орт.
касательной (скалярного произведения)
Из дифференциальной геометрии известно, что
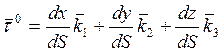
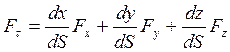
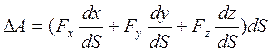
![]() ….. (26)
….. (26)
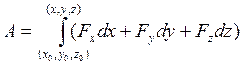 (27)
(27)
Определение работы силы через путь, пройденный материальной точкой.
а)

Пусть точка М движется в сторону положительной траектории координат.
dS>0, S-S0=dS=d![]()
![]()
![]()
![]()
![]() (28)
(28)
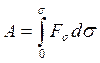
б)

S0>S,
S-S0=dS<0, ![]() (приращение
по пути >0)
(приращение
по пути >0)
![]()
Эл. работа: ![]() - элементарный пусть
материальной точки
- элементарный пусть
материальной точки
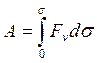 (29)
(29)
Запомнить N.b!: формулы вычисления работы: (23, 24), (26, 27) и (28, 29)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.